Foundation of the New Cell using 3-Dimensional to the Solar Cell

Abstract

This paper proposes a new type of solar electric cell and method to achieve higher power density compared to conventional solar cells. The proposed apparatus and method comprise photovoltaic liquid fluids (eg. colloidal quantum dots/perovskite type fluids) in a flow-cell comprised of high porosity 3-Dimensional metal substrates. Based on several key factors that will be discussed, it is believed that this new cell and process could enable substantially more power per unit geometric panel area compared to conventional solid-state passive 2-Dimensional solar panels. Technical rationale will be analysed for how this method could de facto overcome current power limitations per unit panel area in conventional solar panels (such as Shockley-Queisser and recombination). Proposed fundamental governing mathematical models and associated variables for this new process are provided as a starting point, with the main goal being to illuminate this concept for other scientists and engineers to add their expertise and ingenuity to make such systems a commercial reality if it is practical to do so. A potential real-world application would be an on-board solar charging panel for electric vehicles, and similar applications where space is limited and maximum power density from a solar panel is desirable

Keywords

Solar energy; Photovoltaic cells; Colloidal quantum dots; Perovskite; Shockley-Queisser; Electric vehicles

Introduction

The foundation of the new cell and process begins with a 3-Dimensional approach to the solar cell, and a 4-Dimensional approach to the overall process because flow rate and time are also key aspects of the process. From an overall perspective, dynamic processes in 4-Dimensions (3D space and time) tend to considerably outperform 2-Dimensional passive systems in natural and engineering processes; this paper provides several supporting ideas why this could be true for solar PV electric systems. Hereafter, the electron-generating fluid will be abbreviated as PV fluid and the dynamic cell and process as 4DCPV (Figure 1). It is hypothesized that the 4DCPV power output may theoretically be limited only by the following key factors:

Figure 1: Schematic of the 4DCPV concept.

→ The amount of PV fluid flow that can pass through the 3D cell per unit time.

→ The amount of electrons that the PV fluid can produce per unit time within the cell (via absorption of photon energy to achieve an electron excitation state).

→ The amount of the excited electrons that can successfully conduct out of the cell to achieve useful work before returning to the fluid/cell to complete the circuit (relative to the excited electrons that recombine to their ground-state and do not conduct out of the cell).

A visual description is that 4DCPV comprises a labyrinth of inter-connected metal strands forming a 3D volume filled with electron-generating PV fluid flowing throughout. The cell substrate (the highly conductive metal strands inter-connected as a singular object) is porous enough to allow light to penetrate and impact the PV fluid traversing throughout to create excited electrons yet also comprise sufficient strand density to be immediately available to conduct the sea of excited electrons generated throughout the cell.

Materials and Methods

Modelling 4DCPV system behaviour as a dynamic chemical reaction process

It is useful to derive mathematical models to help understand the potential advantages of the 4DCPV process, as well as help guide predictive system behaviour and optimization. The models chosen for this paper are to equate the 4DCPV process steps to chemical reaction/chemical equilibria style processes and associated equations. There are several major reasons for doing this, as shown in the following examples and rationale:

Consider an example where we have 100 g of reactant in a fixed solid-state 2-Dimensional (2D) surface area. In a one minute time frame, sufficient activation energy is provided for 20% reaction efficiency- yielding 20 grams of product. Now let’s say we have 200 g of the same reactant in a 3-Dimensional (3D) volume, with the identical 2D surface area. Assuming there is sufficient activation energy to still achieve 20% reaction efficiency and all else being equal, the system will have generated 40 grams of product in the same 1 minute time frame.

The above example is a static 1-minute comparison. With 4DCPV, there is a continuous flow of PV fluid (at least, whenever there is suitable activation energy to make the process work). We can conceptualize that if say 300 grams of liquid-phase reactant can pass through the 3D volume (with the same 2D surface area in the example above) in 1 minute, then 20% reaction efficiency would yield 60 grams of product. Alternatively, we can consider that 13% reaction efficiency on 300 grams of liquid-phase reactant would yield 40 grams of product in the 4DCPV process- still 2 times more product compared to the static solid-state 2D surface area process.

Now if we say that the “reaction product” is in fact the electrons (and associated electrical energy output) of a solar energy cell (i.e. the “reactant” is PV fluid that generates electrons upon impact of suitable photon energy, and the “activation energy” comes from the photons provided free from the electromagnetic radiation of the Sun), then the de facto cell efficiency would be 40%-60% for the 4DCPV process compared to 20% for the 2D cell (based on energy output per equivalent 2D surface area of panel).

It is well worth noting that the 4DCPV examples provided above would generate 2 × -3 × the power output per equivalent square meter of panel area even at 13%-20% efficiency (well below the theoretical efficiency of Shockley-Quiesser). In other words, the efficiency of the dynamic 4DCPV process does not violate Shockley-Queisser per unit of photovoltaic material there is just more photovoltaic material units per time exposed to the sun’s irradiance in the 3D flow cell, so the utilization of the sun’s photon energy per 2D panel surface area is effectively increased. By utilizing two or more types of PV fluid in a 4DCPV, each optimized to specific bands of the Sun’s electromagnetic spectrum, it is believed that the 4DCPV process can effectively act as a multi-junction solar cell and exceed the single-junction Shockley-Queisser limits opening up even more possibilities for cell power density.

The above examples provide a chemical process engineering rationale for 4DCPV. A theoretical physics/thermodynamic approach is also useful and necessary in deriving a mathematical model for predictive system behaviour (and how to make the most energetically favourable) 4DCPV process. In deriving these fundamental equations, the electrons are envisioned to follow similar behaviour and rules to chemical reaction/chemical equilibria processes. This hypothesis is based on the fact that much of the behaviour in chemical equilibria is deeply rooted in the behaviour and interactions of the electrons in the associated chemicals, and assumes that the solar PV process can be modelled as a reaction that generates electrons as a product with the Sun’s electromagnetic spectrum providing free activation energy to drive it. So called “driving force” process parameters and associated variables govern chemical reactions and equilibria, and should be a reasonable predictive model for interactions in the dynamic 4DCPV as well [1-4]. This allows for manipulation of the variables and process thermodynamics with techniques such as applying Le Chatelier’s principle.

Both the chemical reaction process engineering and thermodynamic/theoretical physics factors are utilized in deriving the proposed governing equations and selection of optimal process/material parameters for 4DCPV. Ultimately, the goal is to demonstrate that 4DCPV for solar cells can generate more power output per square meter of available surface area, and effectively overcome the current power limitations associated with solid-state [5-8] passive 2D solar (such as the Shockley-Quiesser band-gap limitations of single-junction solid-state semiconductors and re-combination effects with solid state p-n junction layers).

Results and Discussion

Proposed fundamental governing equations and system parameters

Mathematical modelling of the 4DCPV process starts with three fundamental equations written in chemical equilibria style format. In addition to assisting in the derivation of associated variables implicit in the 4D process, these equations will provide insights on how to manipulate the process parameters, variables, and materials to achieve the most energetically favourable 4DCPV process.

The first equation involves writing the interaction between photons and the PV fluid as:

Equation 1:

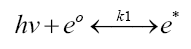
where:

hν=total Planck-Einstein photon energy at one or more incident light frequencies (ν)

e⁰=ground state electrons in the PV fluid flowing through the 3D solar cell

e*=excited electrons from the PV fluid

k1=“reaction rate factor” that measures the rate of formation of “products” (e* in this case) relative to “reactants” (e⁰ in this case) over a given time frame, factoring in any reversion of e* converted back to e⁰

Clearly, the selection of PV fluid(s) for 4DCPV would be those that favor the reaction to the right (the “products” side of the chemical equilibria) upon impact by incident light frequencies.

The second chemical-equilibria style equation in 4DCPV involves the interaction between the excited electrons and the material(s) of the solar cell:

Equation 2:

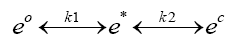
Where:

e⁰=ground state electrons in the PV fluid(s) flowing through the 3D solar cell

e*=excited electrons from the PV fluid

e^c= excited electrons from the PV fluid that are conducted into the cell’s substrate

k2=“reaction rate factor” that measures the rate of formation of “products” (ec in this case) relative to “reactants” (e* in this case) over a given time frame, factoring in any reversion of ec converted back to e*

k1=the reaction rate factor from Equation 1

Equation 2 is presented as a “tug of war” scenario- where the excited electron can revert to a reactant (a ground state electron in the PV fluid of Equation 1) or conduct into the cell’s substrate. Clearly, an optimal 4DCPV process would favour both reactions to the right, and the selection of cell parameters must be such that it “wins” the tug of war at a high enough propensity to be commercially viable. The reaction rate factor k1 will be affected by Equation 1 as well as the efficiency of excited electrons being conducted into the cell (k2).

Equation 2 provides an excellent opportunity to focus on driving forces and manipulations to achieve favourable results by invoking an electrical version of Le Chatelier’s principle. If we assume in Equation 2 that the cell is made of an excellent instantaneous conductor, the chemical equilibria of Equation 2 should be driven very far to the right unless there becomes a surplus of products (ec electrons) in the cell. A highly efficient cell conductor for 4DCPV should accept the excited electrons instantaneously and be able to instantaneously conduct them out of the cell- to continuously “starve” the product’s side (ec) and continuously drive both reactions of Equation 2 favourably “to the right.” Key parameters of the proposed cell to accomplish this will be discussed later in this paper.

The third chemical-equilibria style equation for 4DCPV involves the flow of electrons conducted out of the cell to a staging area (electrical energy storage) until called upon to do electrical work, then returning to the PV fluid to complete the circuit and restore the ground-state electrons for the process of Equations 1 through 3 to repeat.

Equation 3:

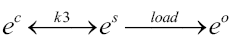
Where:

e^c=excited electrons from the PV fluid that are conducted into the cell’s substrate

e^s=excited electrons that are conducted out of the cell and into a staging/storage system (e.g. capacitors or batteries) before moving on to power an electrical load

e⁰=electrons returning to the PV fluid to complete the circuit and restore ground state for the process of Equations 1 through Equation 3 to repeat

k3=“reaction rate factor” that measures the rate of formation of “products” (es in this case) relative to “reactants” (e^c in this case) over a given time frame, factoring in any reversion of es converted back to e^c

Again, the obvious goal is to drive this series of reactions as far as possible to the right. By utilizing clever arrangements of Capacitor/Battery Storage in Equation 3, it is believed that the ec of Equation 2 can be maintained in the desired “starved” state favourable to the Le Chatelier style process manipulations described above, and in doing so maintain the reverse reactions of Equations 2 and 3 to a minimum.

In conventional 2D solar PV, it is well established that re-combination of excited electrons in the solid-state semiconductor (prior to conducting out of the cell to do electrical work) diminishes the net power output. The 4DCPV process could offer greater options to overcome such limitations; such as with the chemical-equilibria style manipulations described above, a wider variety of process variable manipulations (flow rate, multiple PV fluids, the 3D solar cell parameters…) and by eliminating the need for expensive solid-state multi-junction approaches required to overcome Shockley-Queisser and p-n junction layer issues of passive solid-state 2D PV systems.

These three foundational equations, their driving forces, and their inter-relations set the stage for deriving a governing equation for the 4DCPV process. Since 4DCPV process involves PV fluid flow and time as a variable, the equation that incorporates the net effect of the 3 chemical equilibria-style equations and all related variables must consider system dynamics to predict the performance of the 4DCPV cell. One way to do this is to model the system power for a time frame that represents “one cell volume” of fluid flow:

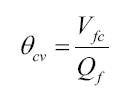
Where:

θ_cv=residence time for one cell volume of PV fluid to pass through the cell

V_fc=volume of PV fluid in the cell=(total geometric volume of the cell–volume of internal cell substrate)

Q_f=volumetric flow rate of the PV fluid through the cell

The proposed governing equation for theoretical maximum 4DCPV instantaneous power of one cell volume becomes: ℵ

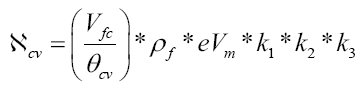
Where:

ℵ_cv=instantaneous power generation of one cell volume of PV fluid

ρ_f=mass density of the PV fluid

eV_m=maximum theoretical electron volt potential/unit mass of PV fluid

k₁, k₂, k₃=the reaction rate factors of Equations 1-3 at steady state under ideal conditions

The time-dependent total energy output for multiple cycles and under various process conditions is modelled as:

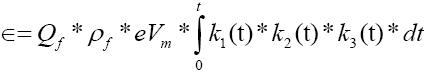
Where:

ϵ=total energy generation of the 4DCPV process under variable conditions from time zero to time (t)

Q_f=volumetric flow rate of the PV fluid

k₁(t), k₂(t), k₃(t)=the time-dependent functions of the reaction rate factors of Equations 1-3 (i.e. as process conditions such as incident irradiance and other variables change over time).

Since the ultimate goal is to achieve a high power density 4DCPV that overcomes current passive 2D solid state solar PV power limitations per unit area of panel, the power and energy output equations can be normalized either by unit volume of the 4DCPV cell or unit 2D geometric panel area that the 4DCPV cell occupies- to compare the power output of 4DCPV in a direct equivalent 2D area that might otherwise be occupied by conventional passive solar panel.

The use of the reaction rate factors (k₁, k₂, k₃) simplify a host of underlying variables to (hopefully) make it easier to see the big picture of the 4DCPV process and how Equations 1-3 are inter-related. For optimizing a 4DCPV process at lab or pilot scale, it is worth contemplating the underlying variables and process parameters within these reaction rate factors:

Implicit variables and process parameters in the reaction rate factors k₁, k₂, and k₃

k₁: The range of photon energies from the source (e.g. the frequency range of the sun’s electromagnetic spectrum). This is of particular interest because 4DCPV opens up the possibility to utilize two or more PV fluids in the same process- each optimized for specific bands of solar energy (e.g. one PV fluid for strong UV absorption, and another PV fluid for strong visible/IR frequency range absorption) as a means to overcome band-gap thermodynamic limitations of one material optimized for a shorter frequency range. If the PV fluids are compatible, they can be mixed together; if not, they can each pass through their own 4DCPV cell and be stacked on top of each other to maximize the energetic use of the full electromagnetic spectrum. Some of the variables to consider include the frequencies (ν) in the incident light, the total irradiance energy of all frequencies in the incident light, and temperature of the PV fluid(s).

The geometric configuration of the 3D solar cell in terms of the cell’s ability to efficiently absorb and harness as much of the available photon energy as possible. Variables to consider include the total porosity, the pore size, and depth of the 3D solar cell.

Fluid-mechanical properties such as volumetric flow rate of PV fluid through the cell, the total volume of PV fluid in the 4DCPV system, and turbulence of flow through the cell.

The degree to which the PV fluid(s) can generate excited electrons upon suitable incident photon energies. In the model of 4DCPV discussed above, this is the eVm quantity (the intrinsic property of maximum theoretical excited electron volt potential per unit mass of PV fluid) and the degree to which this theoretical maximum can be achieved (an extrinsic property dependent on the interaction of the PV fluid with the system parameters of the type described above).

k₂: The electrical conductivity of the 3D cell’s substrate. The rate of flow of excited electrons into the cell’s conductive substrate (to minimize re- combination of excited electrons back to the ground state in the PV fluid). Variables to consider include the structure of the 3D cell (total porosity, pore size, pore depth, geometric arrangement) and turbulence of PV flow through the cell to maximize probability of contact/conductance for excited electrons throughout the entire 3D porous cell labyrinth. A 4DCPV “Reynolds Number” factoring in the fluid-mechanic properties and net cross-sectional flow area (geometric cross-section flow area of the cell minus the area occupied by the cell’s 3D conductor strands) will likely be an important metric for helping maximize the value of k₂ (and k₁ as well).

k₃: This mainly depends on clever capacitor/battery storage design and arrangement, for reasons described above. This staging/storage area is likely to be critical for keeping the dynamic 4DCPV process operating at peak efficiency regardless of whether the system is under load conditions or not. It is notable that any electrical energy needed to power a re-circulation pump for the PV fluid flow can be provided from the 4DCPV process this would be a small but continuous need for power whenever there is sufficient activation energy (photon energy) to drive the process forward. It is notable that natural thermosiphoning could also help drive fluid motion to reduce the electrical energy needed for mechanical pumping.

Conclusions

Practical process needs and materials

The key practical process and materials needed for successful 4DCPV are expected to be

→ Availability of a suitable PV fluid(s) that can achieve sufficient excited electron amounts per unit time at a specified flow rate of the PV fluid through the 3D solar cell. PV fluid candidates for 4DCPV include colloidal quantum dots and Perovskite-type fluids. One or more PV fluids could be utilized for reasons previously discussed.

→ Availability of a suitable 3D solar cell that offers sufficient porosity for the Sun’s photons to traverse throughout, and sufficient conductor contact area and electrical conductivity for instantaneous electrical conductivity of excited electrons. The best known conductive 3D cell candidates are porous copper substrates that have a high degree of freedom for total porosity, pore size, and depth in addition to the extraordinary electrical conductivity inherent in copper. These substrates can be 95%-98% porosity offering the opportunity to do “more with less” as our planet’s resources become more constrained.

→ “Driving Force” electrical and thermodynamic process parameters that are optimized via lab and pilot experiments.

These material candidates, all associated variables, and the mathematical models described above present exciting opportunities for optimizations in search of commercially viable 4DCPV processes.

References

1. Zhou T, et al. Highly efficient and stable solar cells based on crystalline oriented 2D/3D hybrid perovskite. Adv Mater. 2019;31:1901242.

   [Crossref][Google scholar][EBSCO]

2. Lee JW, et al. 2D perovskite stabilized phase-pure formamidinium perovskite solar cells. Nat Commun. 2018;9:3021.

   [Crossref][Google scholar][EBSCO]

3. Quan LN, et al. Ligand-stabilized reduced-Dimensionality perovskites. J Am Chem Soc. 2016;138:2649-2655.

   [Crossref][Google scholar][EBSCO]

4. Mao L, et al. Two-Dimensional hybrid halide perovskites: principles and promises. J Am Chem Soc. 2019;141:1171-1190.

   [Crossref][Google scholar][EBSCO]

5. Li N, et al. Towards commercialization: the operational stability of perovskite solar cells. Chem Soc Rev. 2020;49:8235-8286.

   [Crossref][Google scholar][EBSCO]

6. Shi D, et al. Low trap-state density and long carrier diffusion in organolead trihalide perovskite single crystals. Science. 2015;347:519.

   [Crossref][Google scholar][EBSCO]

7. Johnston MB, et al. Hybrid perovskites for photovoltaics: charge-carrier recombination, diffusion, and radiative efficiencies. Acc Chem Res. 2016;49:146-154.

   [Crossref][Google scholar][EBSCO]

8. Hoke ET, et al. Reversible photo-induced trap formation in mixed-halide hybrid perovskites for photovoltaics. Chem Sci. 2015;6:613-617.

   [Crossref][Google scholar][EBSCO]