Keywords
|
| OFDM, Multi carrier transmission, Carrier Frequency Offset (CFO), Neural Networks (NN), BER ,SNR |
INTRODUCTION
|
| OFDM is a effective multicarrier scheme, OFDM has been adopted by many standards e.g., IEEE 802.11a/g/n, IEEE 802.15.3a, IEEE 802.16, IEEE 802.20 in the US and DAB, DVB, 3GPP Long Term Evolution (LTE) in Europe. OFDM has been adopted in the Wi-Fi where the 802.11a standard uses it to provide data rates up to 54 Mbps in the 5 GHz ISM (Industrial, Scientific and Medical) band. In addition to this the recently ratified 802.11g standard has it in the 2.4 GHz ISM band. In addition to this, it is being used for Wi-MAX. OFDM, by transforming a frequency selective fading channel into a set of parallel flat sub-channels, has got many advantages, namely; it san easily adapt to severe channel conditions without the need for complex equalization, it is robust against narrow-band co-channel interference, robust against intersymbol interference (ISI) and fading caused by multipath propagation, it provides high spectral efficiency, it has low sensitivity to time synchronization errors |
| However, OFDM has the disadvantage of high PAPR (peak to average power ratio) and serious ICI (inter-sub-carrier interference).Especially, the ICI caused by phase noise or frequency offset seriously degrades system performance because it was break down the orthogonality between sub-carriers. CFO's are typically caused by mismatched transmitter and receiver oscillators, or by Doppler shift due to movement. In practice, [1] Carrier Frequency Offset (CFO) destroys the orthogonality of the subcarriers in OFDM systems, and leads to Inter carrier Interference (ICI) among the subcarriers. Consequently, CFO increases the system Bit Error Rate (BER) [2]. Therefore, CFO has to be estimated and compensated in a practical OFDM system. This paper proposes using a Neural Network technique for discriminating the frequencies of the carriers to compensate the effect of the CFO. |
OFDM CHANNEL MODEL
|
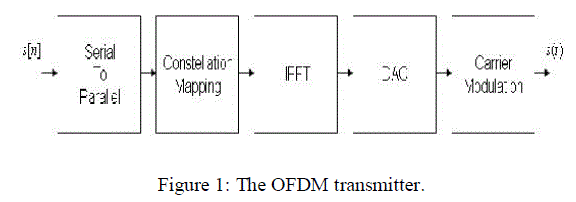
| The OFDM transmitter is presented in figure 1 and the receiver is presented in figure 2. |
 |
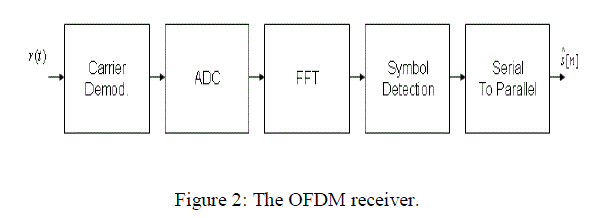 |
| An OFDM carrier signal is the sum of a number of orthogonal sub-carriers, with baseband data on each subcarrier being independently modulated. Commonly, using some type of quadrature amplitude modulation (QAM) or phaseshift keying (PSK). This composite baseband signal is typically used to modulate a main RF carrier. Where, s[n] is a serial stream of binary digits, N is the number of sub-carriers, DAC is a digital-to-analog converter, c f is the carrier frequency and s (t) is the transmission signal, an inverse FFT is computed on each set of symbols, giving a set of complex time-domain samples. These samples are then quadrature-mixed to bandpass in the standard way, r (t ) is the received signal, ADC is analog-to-digital converter, s[n] is an estimate of the original binary stream send by the transmitter and a forward FFT is used to convert back to the frequency domain. If N sub-carriers are used, and each sub-carrier is modulated using M alternative symbols, the OFDM symbol alphabet will consist of M N combined symbols. To avoid ISI in multipath fading channels, a guard interval of length Tg is inserted prior to the OFDM block. During this interval, a cyclic prefix is transmitted such that the signal in the interval −Tg ≤ t < 0 equals the signal in the interval Tg −T ≤ t <T . The OFDM signal with cyclic prefix is: |
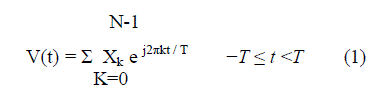 |
| Where Xk are the data symbols and T is the OFDM symbol time. The sub-carrier spacing of 1/T makes them orthogonal over each symbol period. In general, the transmitted signal can be represented as, [1], [2]: |
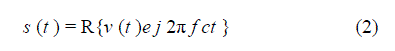 |
DISCUSSION ON FREQUENCY OFFSET
|
| The term frequency offset refers to a non-zero carrier frequency seen at baseband in the receiver. Carrier offsets are caused by imperfect demodulation from RF, as well as frequency drift caused by Doppler shift. Both of these cause the OFDM subcarriers to be viewed at the receiver as slightly different frequencies than intended and must be compensated for in order to avoid either inter-carrier interference. In a typical wireless communication system, the signal to be transmitted is up converted to a carrier frequency prior to transmission. The receiver is expected to tune to the same carrier frequency for down converting the signal to baseband, prior to demodulation. |
| OFDM is extremely sensitive to frequency offsets, given the highly dense spectral characteristics of OFDM. Since the carriers are overlapping on each other, small frequency offsets cause large amounts of interference. |
| However, due to device impairments the carrier frequency of the receiver need not be same as the carrier frequency of the transmitter. When this happens, the received baseband signal, instead of being centered at DC (0MHz), will be cantered at a frequency fΔ , where Y(t) is the received signal |
| X(t ) is the transmitted signal and |
| fΔ is the frequency offset |
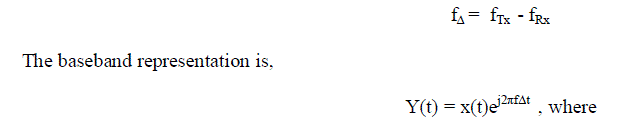 |
THE PROPOSED RBPN NETWORK FOR FREQUENCY OFFSET COMPENSATION
|
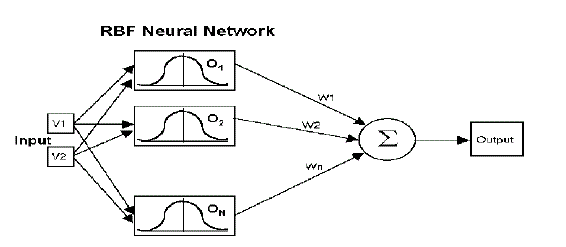
| Radial basis function (RBF) networks typically have three layers: an input layer, a hidden layer with a non-linear RBF activation function and a linear output layer. |
 |
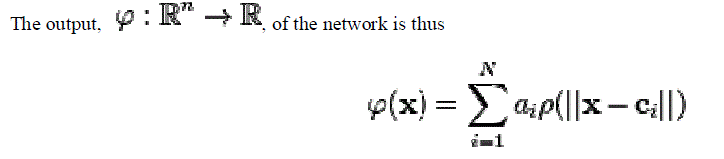 |
| Where , N is the number of neurons in the hidden layer, is the center vector for neuron i, and ai are the weights of the linear output neuron. In the basic form all inputs are connected to each hidden neuron. The norm is typically taken to be the Euclidean distance and the basis function is taken to be Gaussian. |
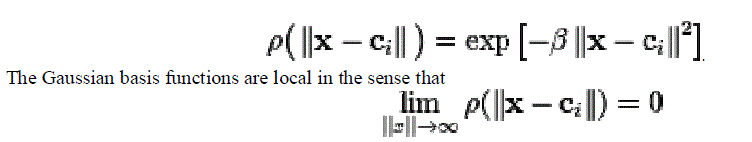 |
| i.e. changing parameters of one neuron has only a small effect for input values that are far away from the center of that neuron.RBF networks are universal approximation on a compact subset of . This means that a RBF network with enough hidden neurons can approximate any continuous function with arbitrary precision. The weights ai, , and β are determined in a manner that optimizes the fit between and the data. |
| Normalized radial basis functions |
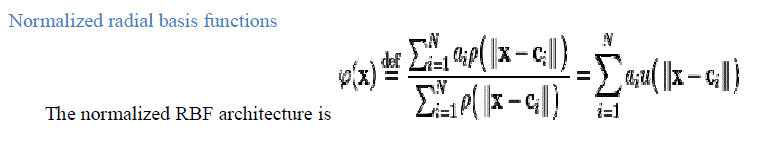 |
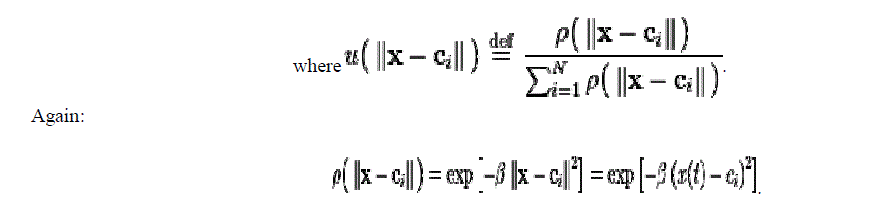 |
| Again, we choose the number of basis functions as five and the size of the training set to be 100 exemplars generated by the chaotic time series. The weight β is taken to be a constant equal to 6. The weights ci are five exemplars from the time series. The weights ai are trained with projection operator training: |
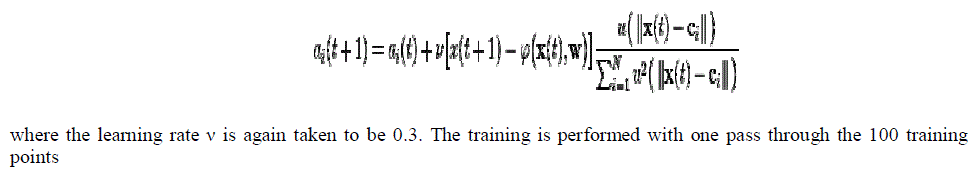 |
SIMULATION SCHEMES AND RESULTS
|
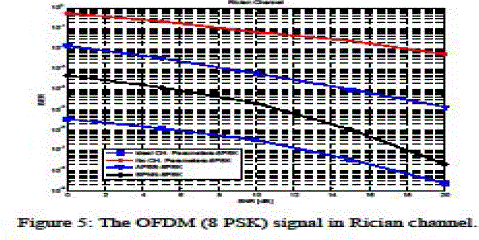
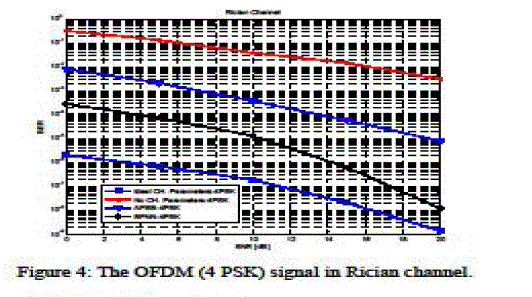
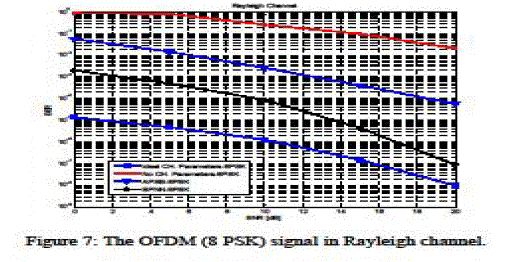
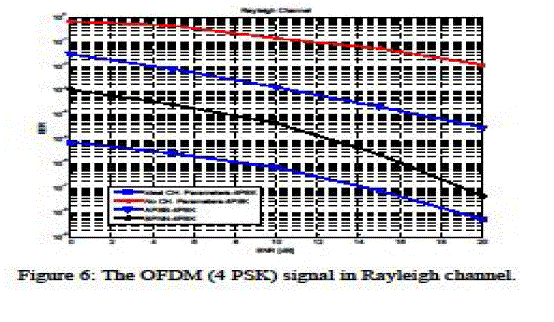
| The simulation is performed under the assumptions that, the channel fading is constant over the frame and independently distributed from one frame to the other and no carriers frequencies offsets (CFO's). In all simulations, all results are averaged over 250 random channel realizations and the processing time is used as a complexity measure. The simulation results, in the presence of Rician fading channel, are presented in figure 4 and 5, in the presence of Rayleigh fading channel are presented in figure 6 & 7. By using multipath channel profile for fixed reception using indoor antenna and channel profile for mobile reception with indoor/outdoor antenna. The simulation is performed using MATLAB R2011. The main parameters are indicated in table 1. |
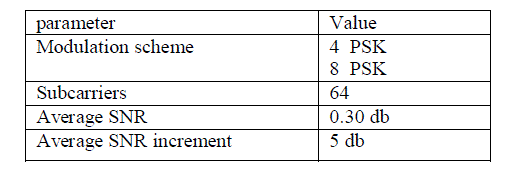 |
 |
 |
 |
 |
 |
CONCLUSION
|
| The paper is dealing with the channel compensation in OFDM systems. The paper proposes using RBPNN to estimate the channel model and then equalize the effect of the channel. The simulation results show that using the proposed RBPNN results in a BER performance enhancement over the considered technique in all considered channel models, namely; Rician, Rayleigh models. But it has a disadvantage which is the computational complexity due to the training algorithm of the neural networks and the small extra R.F. bandwidth requirement |
References
|
- Yuan Liu ,Wasfy B. Mikhael “ High-Performance Blind Carrier Frequency Offset Estimator for OFDM Systems” Department of Electrical and Computer Engineering University of Central Florida Orlando, Florida,, USA 2006 IEEE.
- Sekchin Chang and Edward J. Powers “Blind Estimation Of Frequency Offset in OFDM Systems Using A Nonlinear Adaptive Filter” Dept. of Electrical and Computer Engineering and Telecommunications and Signal Processing Research Center The University of Texas at Austin (Austin) Texas , U.S.A 2000 IEEE.
- Suckchel Yang and Yoan Shin “A Robust Joint Estimator for OFDM Timing and Frequency Offsets Based on PN Codes” ,Soongsil University, 2004 IEEE
- Tsuguhide Aoki, IEEE, and Magnus Sandell,” Analysis of Pilots for Residual Frequency Offset Estimation in MIMO OFDM Systems” IEEE Transaction On Wireless communication, VOL. 8, NO. 3, MARCH 2009 , IEEE
- Mohammad Movahhedian, “ Blind CFO Estimation for Linearly Precoded OFDMA” Uplink Student Member, IEEE, and Rahim Tafazolli, Senior Member, IEEE Transaction On Signal Processing, VOL. 58, NO. 9, SEPTEMBER 2010.
- Yanxiang Jiang, Xiaohu You, XiqiGao” MIMO OFDM Frequency Offset Estimator with Low Computational Complexity” National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, China. 2007 IEEE
- Yingwei Yao, “Blind Carrier Frequency Offset Estimation in SISO, MIMO, and Multiuser OFDM Systems”Member, IEEE, and Georgios B. Giannakis, Fellow, Transaction On Communication, VOL. 53, NO. 1, JANUARY 2005
- Miin-Jong Hao, Member, IEEE” Decision Feedback Frequency Offset Estimation and Tracking for General ICI Self-Cancellation Based OFDM Systems” IEEE TranasactionOn Broadcasting, VOL. 53, NO. 2, June 2007
|