Keywords
|
| PageRank, TrustRank, Fuzzy Logic, Spam, Search Engine, Web Graph. |
| |
| |
I. INTRODUCTION
|
| Spam is an arms race between search engine and spammers, since spammers are constantly coming up with more and more sophisticated techniques to beat search engines. It is a multi-million dollar industry which is trying to fool search engines. Spammers exploit the way search engines work and deliberately manipulate search engine indexes [1, 4]. Everybody that publishes a site on the web wishes that it will be found. And not only this. It should appear in the top 10 of the search engines. Why? Because people often click on the results of the first page only. Even worse, it has been shown, that most users look only at the topmost two links of the result page. Search engines are the entryways to the Web, which is why some people try to mislead search engines, so that their pages would rank high in search results, and thus, capture user attention [4]. There is a lot of money at stake. There is a huge amount of value from getting to the top of the search results. If spammers get their links to the top of the page, billions will see it. |
| So, how deliberately show page in the first few results? There are two ways: Content spamming and Link spamming [1, 11]. Content spamming techniques involve altering the logical view that a search engine has, over the page's contents. This is done by Engineering the page well, understandable by humans and search engines, delivering extra meta-tags for the search engines, using different words, feeding as many keywords as possible, disregarding if they match the topic of the page or not. Keyword stuffing, Hidden or invisible text, Meta-tag stuffing, Doorway pages, Scraper sites are the most common techniques for content spamming. They all aim at variants of the vector space model for information retrieval on text collections. Link spam is defined as links between pages that are present for reasons other than merit. |
| Link spam takes advantage of link-based ranking algorithms, which gives websites higher rankings the more other highly ranked websites link to it [2, 11]. Since people do not link to spam pages freely, spammers trick many of them to point to a spam page. Or make the referencing pages himself under different domains. |
| Many search engines uses PageRank algorithm to rank their search results that take into account the number of incoming links in ranking pages [5, 6]. PageRank assumes each link is a valid vote for a web site. But, some links are not really valid links at all. In practice, the PageRank concept has proven to be vulnerable to manipulation, and extensive research has been devoted to identifying falsely inflated PageRank and ways to ignore links from documents with falsely inflated PageRank [12]. There are many blatant PageRank manipulation techniques. Another problem with PageRank is that it presents a bias against new web sites. |
| To overcome the problems of PageRank, TrustRank idea was developed. The TrustRank algorithm is a procedure to rate the quality of websites. The basic idea is similar to the PageRank algorithm - taking the linking structure to generate a measure for the quality of a page. TrustRank is a semi-automatic process which involves human operators to judge seed sets [3]. Pages are divided up in good (white) pages and bad (black) pages. It is also assumed that good pages seldom points to bad pages [3]. On the other hand bad pages quite often link to bad pages. The ideal trust property is calculated using these assumptions and eventually list the pages according to their probability of being trusted with a score between 0 (bad) and 1 (good). Sometime there may be a situation where we get a page in between |
| good and bad, in such case a human operator fails to correctly assign a proper trust value. For such sites one operator may assign a value 0 and some may 1. Hence this process involves a human sentiment. Our objective is to minimize the effect of human sentiment by using fuzzy logic. Fuzzy logic is inherently better suited for expressing knowledge on the Web, i.e., knowledge that is uncertain, imprecise, and potentially inconsistent [8, 14]. It provides an intelligent computing layer for enhanced data elaboration and reasoning, and fills the gap between soft human-understanding and hard machine-processing. |
II. PRELIMINARIES
|
| A. PageRank |
| PageRank is a link analysis algorithm, named after Larry Page and used by the Google Internet search engine that assigns a numerical weighting to each element of a hyperlinked set of documents, such as the World Wide Web, with the purpose of "measuring" its relative importance within the set [5, 12]. The algorithm may be applied to any collection of entities with reciprocal quotations and references. When one page links to another page, it is effectively casting a vote for the other page [5]. The more votes that are cast for a page, the more important the page must be. Also, the importance of the page that is casting the vote determines how important the vote itself is. |
| A PageRank results from a mathematical algorithm based on the graph, the web graph, created by all World Wide Web pages as nodes and hyperlinks as edges, taking into consideration authority hubs such as cnn.com or usa.gov. The rank value indicates an importance of a particular page. A hyperlink to a page counts as a vote of support. The PageRank of a page is defined recursively and depends on the number and PageRank metric of all pages that link to it ("incoming links"). A page that is linked to by many pages with high PageRank receives a high rank itself. If there are no links to a web page there is no support for that page. |
| PageRank is a probability distribution used to represent the likelihood that a person randomly clicking on links will arrive at any particular page. PageRank can be calculated for collections of documents of any size. It is assumed in several research papers that the distribution is evenly divided among all documents in the collection at the beginning of the computational process. The PageRank computations require several passes, called "iterations", through the collection to adjust approximate PageRank values to more closely reflect the theoretical true value. A probability is expressed as a numeric value between 0 and 1. A 0.5 probability is commonly expressed as a "50% chance" of something happening. Hence, a PageRank of 0.5 means there is a 50% chance that a person clicking on a random link will be directed to the document with the 0.5 PageRank. |
| B. TrustRank |
| It is a technique to semi-automatically separate reputable, good pages from spam [3]. TrustRank is a modification of PageRank and therefore uses the link structure of the web to classify pages. But instead of propagating a Rank of the page it wants to propagate trust. A page is then spam, if it is not trusted from any other page in which we trust. The basic assumption of TrustRank is that good pages usually point to good pages and seldom have links to spam pages. TrustRank method calls for selecting a small set of seed pages to be evaluated by an expert. Once the reputable seed pages are manually identified, a crawl extending outward from the seed set seeks out similarly reliable and trustworthy pages. |
| TrustRank wants to propagate trust. But how do we define trust? And how to propagate it? The idea behind TrustRank is that in beginning a seed set of pages is built, of which we are sure if they are spam or not. All these pages are assigned a trust value in the initial distribution vector d. This value is 1 if the page is good and 0 if not. Now TrustRank starts with the assumption that no page which is non-spam will link to a spam page. Clearly, that is not fully true, sometimes you can be tricked to link to a page, may be by cloaking or page copying. Therefore there are some links between the two sets of spam and non-spam pages. The difficult part of TrustRank is now how to adjust the algorithm such that these links do not get full trust. In the beginning, the developers of TrustRank introduce in a socalled oracle and a machine computed trust-property. The oracle O is a human judging on a page p if it is spam or not. |
| TrustRank Algorithm [3]: |
| function TrustRank |
| input |
| T transition matrix |
| N number of pages |
| L limit of oracle invocations |
| αB decay factor for biased PageRank |
| MB number of biased PageRank iterations |
| output |
| t* TrustRank score |
| begin |
| // evaluate seed-desirability of pages |
| (1) s = SelectSeed(...) |
| // generate corresponding ordering |
| (2) σ = Rank({1,...,N},s) |
| // select good seeds |
| (3) d = 0N |
| for i = 1 to L do |
| d(σ(i)) = 1 |
| // normalize static score distribution vector |
| (4) d = d/|d| |
| // compute TrustRank scores |
| (5) t*= d |
| for i = 1 to MB do |
| t∗ = αB ·T·t* + (1−αB) ·d |
| return t* |
| 1) Oracle and Trust Functions: |
| Determining if a page is spam is subjective and requires human evaluation. We formalize the notion of a human checking a page for spam by a binary oracle function O over all pages p ∈ V [3]: |
| ?? ?? = 0 ???? ?? ???? ?????? 1 ???? ?? ???? ?????? |
| Oracle invocations are expensive and time consuming. Thus, we obviously do not want to call the oracle function for all pages. Instead, our objective is to be selective, i.e., to ask a human expert to evaluate only some of the web pages. To discover good pages without invoking the oracle function on the entire web, we will rely on an important empirical observation we call the approximate isolation of the good set: good pages seldom point to bad ones. This notion is fairly intuitive, bad pages are built to mislead search engines, not to provide useful information. Therefore, people creating good pages have little reason to point to bad pages. |
| However, the creators of good pages can sometimes be “tricked,” so we do find some good-to-bad links on the web. Given a good, but immoderate message board, spammers may include URLs to their spam pages as part of the seemingly innocent messages they post. Consequently, good pages of the message board would link to bad pages. Also, sometimes spam sites offer what is called a honey pot: a set of pages that provide some useful resource (e.g., copies of some UNIX documentation pages), but that also have hidden links to their spam pages. The honey pot then attracts people to point to it, boosting the ranking of the spam pages. |
| Note that the converse to approximate isolation does not necessarily hold: spam pages can, and in fact often do, link to good pages. For instance, creators of spam pages point to important good pages either to create a honey pot, or hoping that many good outlinks would boost their hub score based ranking. |
| To evaluate pages without relying on O, we will estimate the likelihood that a given page p is good. More formally, we define a trust function T that yields a range of values between 0 (bad) and 1 (good). Ideally, for any page p, T (p) should give us the probability that p is good |
III. APPLICATION OF FUZZY LOGIC TO IMPROVE TRUSTRANK
|
| The goal of function SelectSeed is to identify desirable pages for the seed set. As we saw one of the important part of TrustRank algorithm is to select good seeds. Because the trust score assigned to these seed pages propagate to other pages according to link structure of web graph. A wrong selection of seed page can lead to a different result. Here in basic TrustRank algorithm a single oracle function checks all the aspects of a page in order to check if a page is spam or not. |
| As we see the TrustRank is a semi-automatic process which involves human operators to judge seed sets. Sometime there may be a situation where a operator find a page in between spam and good page, that is this page contain some relevant content along with content that annoy users. For example, a website that provides free eBooks download facility to its users. These websites usually also allow it’s users to download some copyrighted and banned books. These sites seem to be very useful for students but in view of authors and publishers of book these sites are illegal. In this situation a human sentiment involve in deciding a page is spam or not. So this involvement of human operator may alter the TrustRank result. |
| The Fuzzy Logic approach minimizes the involvement of human sentiment by employing different oracle function to check different aspect of a page. Now we have experts for each aspect who assigns a trust score between 0 and 10, based on the spam content of a page. Once we get the output from all the oracle functions we fuzzify these values to get the overall trust score of a page. Finally we propagate these trust scores to other connected pages according to link structure. |
IV. EXPERIMENTS AND RESULTS
|
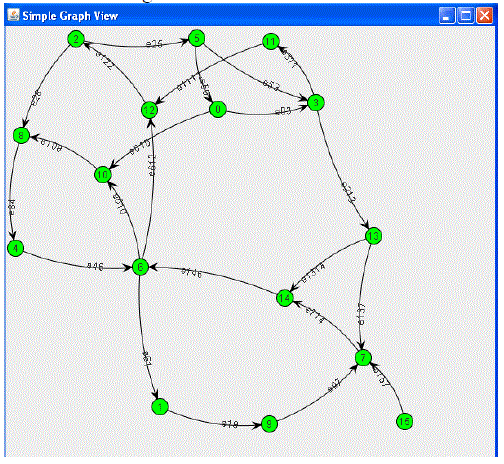
| First, we implemented the TrustRank algorithm on a sixteen node web graph as shown in figure 1. We explain the algorithm by walking through its execution on Figure 1. |
| As a first step, the algorithm calls function SelectSeed, which returns a vector s. The entry s (p) in this vector gives the “desirability” of page p as a seed page. As we have two methods to select seed, we have chosen the seeds with high PageRank version. SelectSeed returns the following vector on the example of Figure 1. |
| s = [0.0090, 0.026, 0.026, 0.027, 0.038, 0.041, 0.054, 0.056, 0.066, 0.074, 0.076, 0.076, 0.085, 0.092, 0.097, 0.159] |
| In step (2) function Rank(x,s) generates a permutation x` of the vector x, with elements x`(i) in decreasing order of s(x`(i)). In other words, Rank reorders the elements of x in decreasing order of their s-scores. For our example, we get: |
| σ = [6, 8, 4, 14, 12, 7, 2, 10, 9, 1, 5, 3, 0, 11, 13, 15] |
| Step (3) invokes the oracle function on the L most desirable seed pages. The entries of the static score distribution vector d that correspond to good seed pages are set to 1. Here we have 16 nodes, hence we chose one by fourth node as seed to be manually evaluated by oracle function Assuming that L = 4, the seed set is {6, 8, 4, 14}. Our oracle function finds Pages 6, 4 and 8 are good seeds and page 14 is a spam page. Now we get the following static score distribution vector for our example: |
| d = [0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 1.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0] |
| Step (4) normalizes vector d so that its entries sum up to 1.Now we have following normalized static score distribution vector for our example: |
| d = [0.0, 0.0, 0.0, 0.0, 0.33, 0.0, 0.33, 0.0, 0.33, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0] |
| Finally, step (5) evaluates TrustRank scores using a biased PageRank computation with d replacing the uniform distribution. Note that step (5) implements a particular version of trust dampening and splitting, in each iteration, the trust score of a node is split among its neighbors and dampened by a factor αB. |
| Assuming that αB = 0.85 and MB = 20, the algorithm computes the following result: |
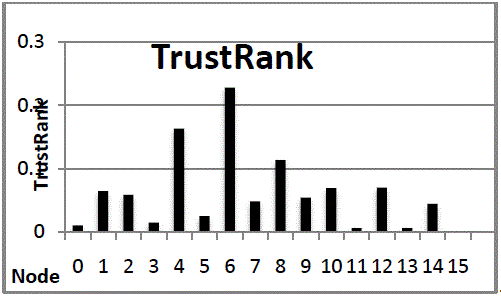
| t* = [0.0108, 0.0647, 0.0591, 0.0154, 0.1632, 0.025, 0.2279, 0.0487, 0.1334, 0.0545, 0.0694, 0.0066, 0.0702, 0.066, 0.0445, 0.0] |
| Analyzing the TrustRank score we notice that because of the way we iteratively propagate trust scores, the good seed pages (namely, 6, 8 and 4) no longer have a score of 1. However, they still have the highest scores. Also notice that good seed page 8 has a lower score than good seed page 4. This is due to the link structure in this example: page 4 has an inlink from a high scoring page (page 8), while page 8 does not. Thus, TrustRank algorithm also “refines” the original scores given by the oracle, determining that there is even more evidence that page 4 is good as compared to 8. Node 15 was not among the seeds, and it did not have any inlinks through which to accumulate score, so its score remained at 0. All good unreferenced web pages receive a similar treatment, unless they are selected as seeds. |
| A. TrustRank Drawbacks |
| The performance of TrustRank can be affected by the selection of the seed set and the determination of the seed distribution in the link graph. Sometime there may be a situation where an operator fined a page in between spam and good, in these cases an oracle function fails to assign proper trust value to a page. Some operator may assign a value 0 and some may assign 1. This dependency on oracle may alter the final TrustRank result and ranking. |
| Consider the implementation of TrustRank on 16 node web graph discussed above. We have seed set {4, 6, 8, 14} and oracle invocation finds Pages 6, 4 and 8 are good seeds and page 14 is a spam page. |
| Now we apply a different oracle on same seed set {4, 6, 8, 14} and finds that page 14 is a good page along with pages 4 and 6 but page 8 is a spam instead. |
| Now we have following static score distribution vector. |
| d = [0.0, 0.0, 0.0, 0.0, 0.33, 0.0, 0.33, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.33, 0.0] |
| Assuming that αB = 0.85 and MB = 20, the algorithm computes the following result: |
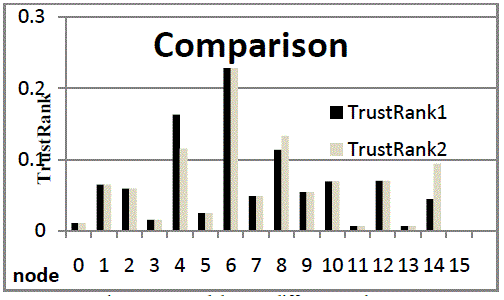
| t* = [0.0108, 0.0647, 0.0591, 0.0154, 0.1154, 0.025, 0.2279, 0.0487, 0.1334, 0.0545, 0.0694, 0.0066, 0.0702, 0.066, 0.0945, 0.0]. |
| Comparing the results from same seed set but inspected by different oracle functions we get that some pages got high TrustRank than previous one and some got low. Analyzing the results now we see that TrustRank of page 14 is much higher than previous result. Also page 8 now have more Trust than page 4. Hence we find that the seed inspected by different oracle function gives different result and also alter the ranking of pages. |
V. FUZZY LOGIC APPROACH TO TRUSTRANK
|
| Fuzzy logic idea is similar to the human being’s feeling and inference process [13]. It allows for approximate values and inferences as well as incomplete or ambiguous data (fuzzy data) as opposed to only relying on crisp data (binary yes/no choices). |
| We want to keep the seed set reasonably small to limit the number of oracle invocations. In order to minimize the number of oracle invocations we have taken into account the following three aspects of a page: |
| ? Spam content |
| ? Unrelated links |
| ? Automatic redirect |
| Now we define linguistic variables and assign membership value to each of these aspects. Input variables: |
| VAR_INPUT |
| spam_content: REAL; |
| unrelated_link: REAL; |
| redirect: REAL; |
| END_VAR |
| Output variable: |
| VAR_OUTPUT |
| trust: REAL; |
| END_VAR |
| Now we define Linguistic term and membership for each linguistic variable. |
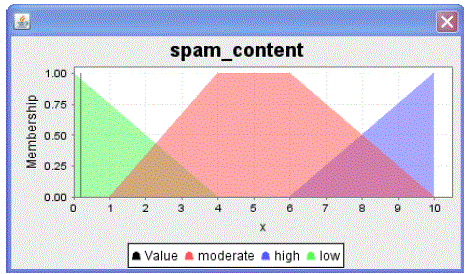
| Linguistic term and membership for spam content: TERM low: = (0, 1) (4, 0); TERM moderate: = (1, 0) (4, 1) (6, 1) (10, 0); TERM high: = (6, 0) (10, 1); |
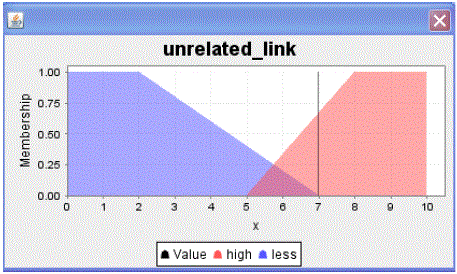
| Linguistic term and membership for unrelated link: TERM less: = (0, 1) (2, 1) (7, 0); TERM high: = (5, 0) (8, 1) (10, 1); |
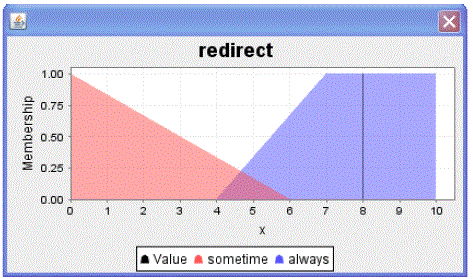
| Linguistic term and membership for redirect: TERM sometime: = (0, 1) (6, 0); TERM always: = (4, 0) (7, 1) (10, 1); |
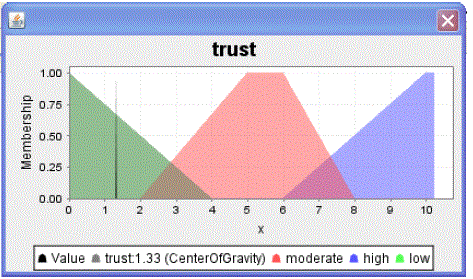
| Linguistic term and membership for output trust: TERM low: = (0, 1) (4, 0); TERM moderate: = (2, 0) (5, 1) (6, 1) (8, 0); TERM high: = (6, 0) (10, 1); |
| Finally we define 36 fuzzy rule sets on the linguistic variables as: |
| RULE 1: IF spam_content IS low OR unrelated_link IS less THEN trust IS low; |
| RULE 2: IF spam_content IS moderate THEN trust IS moderate; |
| Oracle function rates each aspect of a page on a scale of 0 to 10. These values then fuzzified to get a single value. |
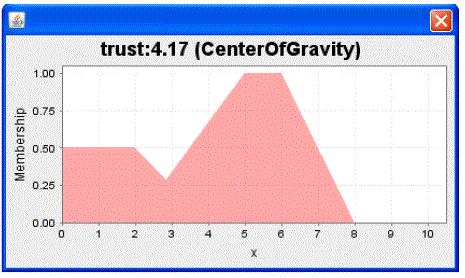
| For example suppose a seed get following value by different oracle functions |
| Inputs: |
| Spam content = 4 |
| Unrelated link = 7 |
| Redirect = 3 |
| After fuzzifying these values using the above rule set we get trust of that seed. Output: Trust = 4.17 |
| In similar way we can choose seed for our 16 node web graph shown in figure 1 above |
| Initially we have chosen seed set {4, 6, 8, 14} according to high PageRank values. Now we employ three oracle functions to manually inspect the seed set for each aspect discussed above. |
| Our first oracle that checks the spam content assigns values {2, 6, 3, 7} to seed set {4, 6, 8, 14}. |
| Second oracle that checks the unrelated link assigns values {4, 2, 2, 4} to seed set {4, 6, 8, 14} |
| And third oracle that checks the automatic redirect assigns values {6, 5, 2, 3} to seed set {4, 6, 8, 14}. |
| We fuzzify these three values for each seed in the seed set using the input membership functions. In next step we combined the fuzzified inputs according to the fuzzy rules to establish rule strength. We get consequence of the rule by combining the rule strength and the output membership function. Combining the consequences we get an output distribution, and defuzzifying the output distribution we get final trust values 4.35, 4.92, 5.09 and 4.93 for seeds 4, 6, 8, 14 respectively. |
| Finally we normalize these values and propagate it to other pages according to link structure of web graph. |
VI. CONCLUSION
|
| The oracle function of TrustRank algorithm only assigns crisp values (0 or 1) to the seed set pages. It doesn’t take into account pages that are in between a spam and a good page. We believe that our work is a first attempt at formalizing the problem and provide a comprehensive solution to assist in the detection of web spam using fuzzy logic. In contrast with traditional oracle invocation, where oracle assigns either 0 or 1 to a page, fuzzy logic approach allows a truth value that ranges in degree between 0 and 1. We reveal that a deeply analyzed seed set can achieve a better performance than a seed set whose all aspects are analyzed by single oracle function in detecting web spam. Use of fuzzy logic for making the Web more intelligent is a slow one, and a major issue is the lack of connection between fuzzy logic and world of Web. Our work bring these two worlds closer together, and thus trying to make the Web more intelligent. |
ACKNOWLEDGMENT
|
| I would like to thank all the faculties and other staff of Department of Computer Science, B.I.T. Mesra, Ranchi, for their cooperation and encouragement. |
| |
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
 |
 |
 |
 |
| Figure 5 |
Figure 6 |
Figure 7 |
Figure 8 |
|
| |
References
|
- Gyongyi, Z. and Garcia-Molina, H., Web spam taxonomy. First International Workshop on Adversarial Information Retrieval on the Web (AIRWeb), 2005.
- Becchetti,L.,Castillo,C., Donato, D., Baeza, R., Leonardi, L., Link analysis for Web spam detection., AIRWeb 2006 workshop, 2006.
- Gyongyi, Z., Garcia-Molina, H. and Pedersen, J., Combating web spam with trustrank, In VLDB Proceedings of the Thirtieth international conference onVery large data bases, VLDB Endowment, 2004.
- Levene, M., An introduction to search engines and web navigation, Wiley & Sons, Inc., Hoboken, New Jersey, pages 209-272, 2010.
- Page, L., Brin, S., Motwani, R., Winograd, T., The PageRank citation ranking: Bringing order to the web, Stanford Digital Library Technologies Project,1998.
- Brin, S., Page, L, The Anatomy of a Large-Scale Hyper textual Web Search Engine, Computer Network and ISDN Systems, Vol. 30, pages 107-117, 1998.
- Krishnan, V. and Raj, R., Web spam detection with antitrust rank, In AIRWeb’06, 2006.
- Timothy J. Ross., Fuzzy Logic with Engineering Applications, Third Edition, Wiley & Sons, Inc., Hoboken, New Jersey, pages 15-168, 2010.
- Gyongyi, Z. and Garcia-Molina, H., Seed selection in TrustRank, Tech. report. Stanford University, 2004.
- Jiang, Q., Zhang, L., Zhu, Y., Zhang, Y., Larger is better: Seed Selection in Link-based Anti-spamming Algorithms, WWW 2008, Beijing, China, 2008.
- Spamdexing, http://en.wikipedia.org/wiki/Spamdexing.
- The Ranking of pages via search engines: http://en.wikipedia.org/wiki/PageRank.
- Bai, Y., Zhuang, H., Wang, D., Advance fuzzy logic technologies in industrial applications, Springer, 2006.
|