Keywords
|
| Fuzzy Diet, Diet Journal, Fuzzy Nutrition, Fuzzy Ontology, Food Recommendation, Diet Planning |
INTRODUCTION
|
| Although understanding the potential biological impact of a specific food choice is as easy as performing a search of articles with the relevant terms, a comprehensive understanding of all potential diet impacts in real time is more complicated. For instance, someone may be on a low fat diet in order to lose weight. That person may be so focused on the reduction of fat that he or she misses other variables in the diet, such as not consuming enough other nutrients. This is where diet journaling and analysis is beneficial. |
| Because the consumption of nutrients may be considered a control system, this is a case where a fuzzy system would be useful. Past work has been performed in this area. For instance, other systems utilize fuzzy ontology to recommend healthier foods based on preference and condition [5][9], [10], and [12]. |
| The goal of this project is to review fuzzy methods in relation to diet journaling, and implement some form of fuzzy system for diet feedback or planning. A nutritional model will be extracted from the literature, with fuzzy values assigned accordingly. |
| The remainder of this paper is divided into 6 sections. Section II provides a brief overview of the core concepts used in the paper. Section III performs a review of the use of fuzzy logic in nutrition systems. Next, section IV discusses the strengths and weaknesses of the related work in terms of how well each work describes the problem space. Each subsection covers a particular issue, and concludes with a well justified, evidence-based conclusion on the direction this paper will take. Section V explains how the fuzzy inference is built for this paper. Section VI explains its implementation and integration with existing diet journaling software. Section VII compares the usefulness of the fuzzy system with various crisp methods, and VIII provides a conclusion on the success of fuzzy methods, with further suggested research. |
II. BACKGROUND
|
A. Fuzzy Set Theory
|
| Fuzzy sets were first proposed by Zadeh in [1] as a way to express degrees of membership to a set in vague, rather than crisp, terms. He later expounded by suggesting the use of fuzzy sets to represent possibility distributions, related to probability distributions via the possibility/probability consistency principle [2]. These principles are exploited in this work. |
| B. Fuzzy Ontology |
| Ontology is a method for representing a piece of knowledge (e.g. an idea, fact, or concept) and its relationship to other pieces of knowledge [3]. Because classical ontology is not equipped to deal with uncertainty or vagueness, they are extended with fuzzy data to compose fuzzy ontology: A fuzzy ontology adds a degree of truth to an ontology, which describes the degree to which an item is an instance of a class of items [4]. This is useful for constructing a set of knowledge for a domain, and running some automated reasoning process on that knowledge which takes into account the aforementioned memberships/relationships. |
A. Fuzzy Concepts in Nutrition
|
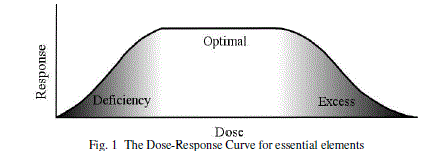
| Fuzzy set theory is very suitable for diet analysis because the effects of nutrient intake are continuous valued; there are no crisp quantities above or below which a nutrient should or should not be consumed, as is demonstrated in the dose-response curve shown in figure 1 [15]. Additionally, any reasoning based on nutrient consumption must be based on scientifically derived empirical data, as this is the only useful means of confirming material knowledge. It is well established that although mathematical concepts may be proven with certainty, material observations may never reach absolute certainty, and therefore scientific conclusions are best expressed in degrees uncertainty, or fuzziness, depending on the conclusiveness of the data. |
III. BACKGROUND
|
A. Research Methodology
|
| In order to assess the state of the art of fuzzy systems applied to diet information, a search of the IEEE Xplore database was performed with the keywords “fuzzy” and “diet”. 14 articles were returned, of which 7 articles were specifically related to assessing the healthiness of a diet [6]. Additionally, a search of “fuzzy” and “nutrition” was performed, which yielded an additional 2 related articles [13]. An additional article of topicality ([15]) was found by reference in [14], and was added to the review set. A brief synopsis covering each of these 10 studies follows. |
B. Summary of Related Works
|
| [5] Focuses on diabetes management. It utilizes a T2FO to construct three 6-layer T2FOs: |
| 1. A fuzzy personal profile ontology which includes region, age, gender, height weight, eating habits, and more. Layer six groups the user into demographics, such as: “Boy”, “Extra slim”, “Big”, etc. |
| 2. A fuzzy food ontology that for each food represents data on food group and macronutrient content, which reduces to calories being high, medium, or low. |
| 3. Fuzzy personal food ontology composed of two sets, planned and actual diet, that eventually resolves to whether very much or very little was eaten, or should be eaten. |
| The system allows a domain expert to enter diet goals and food items. A user, who has a profile, then inputs eaten items. The set of T2FOs defined above, based on these inputs, is consulted by an “Intelligent Diet Recommendation Agent” to create a personalized meal plan that contains suggested servings from the six food groups. |
| [6] involved the Creation of a diet ontology using fuzzy modeling language (FML). It included logic based on Fuzzy inference from fuzzy variables, fuzzy terms, and membership functions on fuzzy sets, and gives the user an indication of healthiness. Healthiness is divided into five states: VeryUnhealthy, UnHealthy, MediumHealthy, Healthy, and VeryHealthy. These classifications were made by the system and then by domain experts independently. The results of the study compared the performance of the system with that of domain experts |
| In [7], a chromosome is constructed to encode FML ontology with many genes containing: the knowledge-base, fuzzy rulebase, and fuzzy hedges. The knowledge-base is constructed with data from Taiwanese foods. A category layer for foods classifies them with respect to how they comprise a meal (e.g. “side dish”, “dessert”, or “Beverage”). Much like in [6], a healthiness level is established, though in this case it is constructed with different inputs, namely the three major macronutrients (carbohydrate, protein, and fat) translated into percentage of total calories: percentage from carbohydrates, protein, and fat (PCC, PCP, and PCF), respectively. A balance of defined food groups, or food group balance (FGB) is computed. A planned calorie vs. consumed calorie ratio (PCR) is computed from actual calories divided by planned. These five inputs: PCC, PCP, PCF, FGB, and PCR, are used in fuzzy rules to map to low, medium, and high fuzzy terms, dietary health level (DHL). To test the system, seven students enter their diet data and the system is evaluated by domain experts. The genetic system is trained and evaluated by experts. |
| In [8], a system much like [5] is constructed, only with a 5-layer fuzzy ontology instead of six, and group information, PCC, PCP, PCF, and FGB, used as inputs just like [7], but excluding PCR, and including caloric density (CD), which is an expression of calories per gram of food consumed. There is also a user profile input like in [3], but it only includes body mass index (BMI) categories: Underweight, Normal, Overweight, and Obese. The output, also as in [7], is a DHL. |
| Similarly, in [10] a three-layer T2FO is constructed with layers consisting of Domain, category, and concept layer, with item and nutrition facts sub-layers. The output is also DHL, and focuses on the possibility of healthy diet status. |
| In [9] and [12], improved diabetes maintenance was sought by means of food clustering using the Taiwan Department of Health (DOH) database as a basis for dietary data. In [9] , experts ranked the importance of each nutrient to diabetics, and in [12], experts determined optimum ranges for each nutrient for diabetics. This rank was used as a weight multiplied against the total amount of a nutrient, for each nutrient in each food, to give a total score for each food. Then, agglomerative hierarchical clustering algorithm (HCA), based on average (rather than complete or single) linkage distance was used to create hierarchical clusters, which were then assigned to classes (synonymous to, but more relevant than “food groups”). Then, foods were ranked within each class using two methods: level positioning, and granular ranking, depending on amount of nutrient and recommendation of nutrients, respectively. The level positioning method was based on seven major nutrients: Calories, moisture, protein, fat, carbohydrate, fiber, and cholesterol. Each food item has its nutrient values for the seven nutrients ranked into three categories: low, medium, high. The granular ranking was based on a positive or negative effect of each nutrient with regard to diabetes care. In this way, food items are grouped by nutrients they contain, and then ranked by the positive vs. negative health impact of each nutrient. In [9], this information was only used to generate a food ontology naming tree, and in [12], the ontology naming tree was implemented in a food substitution recommendation system. A user of the system would enter their weight, and the system would use this and the dietary needs of diabetics to calculate required nutrients, presenting the user with a set of food recommendations. If the user dislikes a food, that food may be removed and the system finds a replacement using the ontology naming tree. |
| In [11], blood glucose level (BGL), diet exercise and insulin regime (DEI), and X (stress, illness, pregnancy, etc.) are used as inputs in an artificial neural network (ANN) to learn the best DEI regime for optimization of BGL. Training of an “Elman” three-layer ANN with 95 neurons in the recurrent layer was performed using back propagation, where the recurrent layer used a tan-sigmoidal function and the output layer used a linear function. Training was performed on a small set of data, and two subjects were found to test validity of the ANN’s output. Included are suggested neuro-fuzzy techniques be used in the future. |
| An expert-driven custom food database is used in [13]. Nutritionists enter data with fuzzy values describing possible imprecision. Diabetic users enter their age, height, weight, physical activity, and diagnoses for a user profile. They then enter their foods and quantities consumed. Considered imprecisions in this process comes from three places: (1) varieties of foods that have only one entry in the database, (2) nutritionist guesses at nutrients contained in foods that have not been analyzed, and (3) measurement error by the user. These are all treated as trapezoidal fuzzy intervals, and are added using fuzzy arithmetic in computing a user’s daily intake of each nutrient, resulting in a vector of fuzzy numbers that is compared to the nutritionist-determined normal intake of nutrients (also a trapezoidal fuzzy interval). The result is shown to the user as a Galvameter after their diet entries, and suggestions about slight changes to the diet are made using a balancing algorithm. |
| Sandham etl. [11] implement a fuzzy inference system (FIS) to estimate the densities of foods using the two inputs: cooking temperature and cooking time. The rules are based on empirical evidence gathered by performing several experiments on frying pre-processed French fries. The results are compared with a test set and the mean error of the system was 2.2%. |
| The system in [15] treats nutrient intake like a dose-response curve in linguistic variables that include: clinical, critical, sufficient, and optimal, for each nutrient. Membership values from 0 to 1 are based on German nutrition recommendations of 6 nutrients for an individual between 25 and 51 with light level of activity and average body weight. Upper limits for cholesterol, alcohol and sucrose are also considered, with membership functions not starting at 0. A hamming distance is defined based on “kitchen units”, which are roughly analogous to serving size that can be used to suggest the amount of change to diet necessary. It is suggested that in order to resolve conflicts in foods that may contain one nutrient but not the other, a harmonic mean operator could be used on each nutrient to determine a Prerow value (PV), which could be used to determine optimal intake of a particular food item, and could be used to suggest small dietary changes. There is no system produced in [15]; it points out a hypothetical use of fuzzy sets for diet analysis |
| Table I below presents a summary of all the past work covered in the preceding synopsis. |
IV. DISCUSSION
|
A. Food Classifications
|
| The food classification approach in [5] results in unjustified boundaries. Two examples are: the food group and region classifications. Food group members can have significant differences, which makes this category less useful than nutrient content [9] , an issue recognized and mitigated in [12]. Additionally, foods in different groups may be similar in nutrient content. For instance, a goal to increase protein consumption can be met just as easily using dairy as with meat, or even a combination of grains and legumes. Analyzing whether the other macronutrients contained in these foods (fat and carbohydrate content) will fit in the food plan is much more relevant than food groups. |
| Additionally, distinguishing features between foods which should exist are not defined, resulting in a myopic system. For instance, the “Grains and Starches” group in [5] does not discern whether a food is whole grain. Because the nutrient content excludes fiber, this information is completely absent. Fiber and whole grains are an important component in controlling diabetes [21] the goal of the systems in these articles. Additionally, micronutrients that are significant in the onset and control of diabetes [17] are excluded from these T2FO systems. As in the previous point, reducing foods to a set of known constituents is more descriptive than these artificial classifications, as it includes important differentiations between foods. |
| A final reason to discard food classifications is that food is broken down into its constituents during digestion, begging a reductionist approach. For the reasons above, the system in this paper will use constituent nutrients and elements, rather than any food groupings, to analyze each food. In this way, rather than developing a complex system with a variety of weak points, a robust and reductionist system will be built that operates on known information. |
B. Hierarchy of Evidence
|
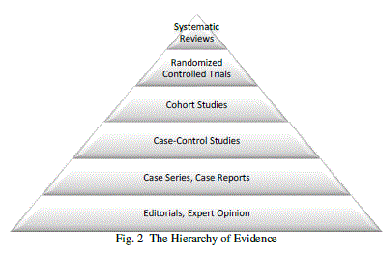
| Expert opinion was used to populate the fuzzy systems in [5]. This type of data occupies the lowest rung in the hierarchy of evidence [24], shown in Figure 2. It is infected with bias, conflict of interest, disagreement, and is considered useful only when evidence is weak [25]. The system in [5] accounts for expert opinion uncertainty using a T2FO. However, this level of uncertainty is unnecessary when systematic reviews and meta-analysis are available [24]. The use of such low quality data more than offsets any potential gains from the use of a Type-2 fuzzy system to express uncertainty. Note that these systems were evaluated based on user satisfaction reporting from a single group of participants. A more results-oriented approach would compare diabetes management success in two groups (one group that uses the system, and a control group that does not). This lack of empirical feedback explains how the previously described deficiencies would go unnoticed by the authors. |
| The systems in [11] and [14] relied on direct observation and empirical analysis, which is an improved position in the evidence hierarchy, but these systems have limited applications. The study in [15] based its food analysis on systematic reviews performed by the German Nutrition Society (DGE), the National Academy of Sciences (NAS), and United States Department of Agriculture (USDA). This evidence is at the apex of the evidence hierarchy, as it is derived from systematic reviews and meta-analysis [24], which constitutes a summation of hundreds of empirical studies. Because of the wealth of studies, this article was able to produce a system that operates on a decent set of nutrients, and the resulting system was much less limited than [11] and[14]. Likewise, the system in this paper will use a comprehensive list of nutrient recommendations available from the USDA. |
| In [6] there is no feedback to the user on how to correct an undesirable level of healthiness. For the system to be useful in improving health, it needs to present actionable feedback to the user. The strength of [5] is that they present the user with changes the user may implement, which is one of the goals of the system in this paper. Therefore, the system will suggest foods based on nutrient content. This paper will borrow concepts from the clustering methods in [9] and[12] to determine which foods to suggest. It will also allow the user to mark a food as undesirable to get another recommendation, an additional concept borrowed from [12]. |
C. Use of Fuzzy Systems
|
| Because the intake of essential nutrients can be treated like a dose-response curve, where there is a range of sufficient intake, but also insufficient and potentially toxic amounts on either end, fuzzy logic provides an extremely well-suited representation of this data [15]. Therefore, it is clear that some form of fuzzy system should be used. Although [9]], [11] and [12] suggest using fuzzy systems in their conclusions, these works do not rely on fuzzy logic. [5] use Type-2 Fuzzy Ontologies, which is supposed to represent uncertainty in expert opinion. Because more certain data is being used for the system in this paper, a Type-2 system is not necessary for this specific rationale, but could be useful in the future if we were to begin encoding less reliable information. In [13], fuzzy intervals were used to represent uncertainty in the nutrient contents of a food and in measurement error, and fuzzy arithmetic was used to compare daily nutrients against a normal profile determined by experts. These uncertainties are guesses rather than based on established research as was performed in [15]. Because of the goal to reflect reality as closely as possible, the system in this paper will show partial memberships based on similar classes to those defined by the dose-response curve in [15], and values from systematic reviews in scientific literature. |
D. Requirements
|
| The requirements in table II are derived from the above discussion: |
A. Input fuzzy sets
|
| Given the previous conclusion that individual nutrients are the best choice for the system, the input set consists of the values for each nutrient consumed. The linguistic values are the level of each nutrient consumed: Inadequate, adequate, and excessive. |
| Each nutrient has a separate mapping onto linguistic values, constructed in the following manner: An intake value of 0 has an inadequacy value of 1.0 for any essential nutrient. For nutrients that are not essential, there is no inadequate set. The adequate set for essential nutrients is a triangular function based off the function triangle (0, x, ul), where x is either the adequate intake (AI), or the recommended daily allowance (RDA), depending on which is available, and ul is the upper limit (UL) designation for the food. For adult intake of macronutrients, the set is a trapezoidal function of the form trapezoid (0, amdr_min,amdr_max,ul) where the acceptable macronutrient distribution range (AMDR) has boundaries amdr_min and amdr_max. |
| These values were determined based on Dietary Reference Intake (DRI) values [26]. Based on comprehensive reviews by the NSA, the USDA has issued DRI values, established to replace the Recommended Dietary Allowance, for known nutrient values. These include the following information: Estimated Average Requirements (EAR) includes the nutrients thought sufficient for at least 50% of the population in a demographic. Recommended Daily Allowance (RDA) is computed to meet the needs of 97% of the population; Adequate Intake (AI) is a less firm belief than EAR or RDA that a food will satisfy everyone in a demographic. Tolerable upper intake levels (ULs) are established for vitamins or nutrients that are known to be toxic above a certain level. The UL is the highest level known to be safe. Lastly, Acceptable Macronutrient Distribution Ranges (AMDRs) specify ranges of macronutrients that are associated with reduced risk of chronic disease [26]. The values were extracted from a table and placed into a database. Values are by age, gender, and for females can differ based on pregnancy and lactation. Some values were not in the USDA DRI’s, and were addressed as follows: Cholesterol, Trans fats and saturated fats do not need to be consumed [26], and so an AI value of 0 was added for each. It is suggested that trans fats should constitute less than 1% daily caloric consumption [27], so an upper limit of 2 grams was placed on this value (based on an 1800 calorie diet). No more than 10% of calories (20g for 1800 calorie diet) should be from saturated fat, and no more than 300 mg of cholesterol should be consumed per day [28]. |
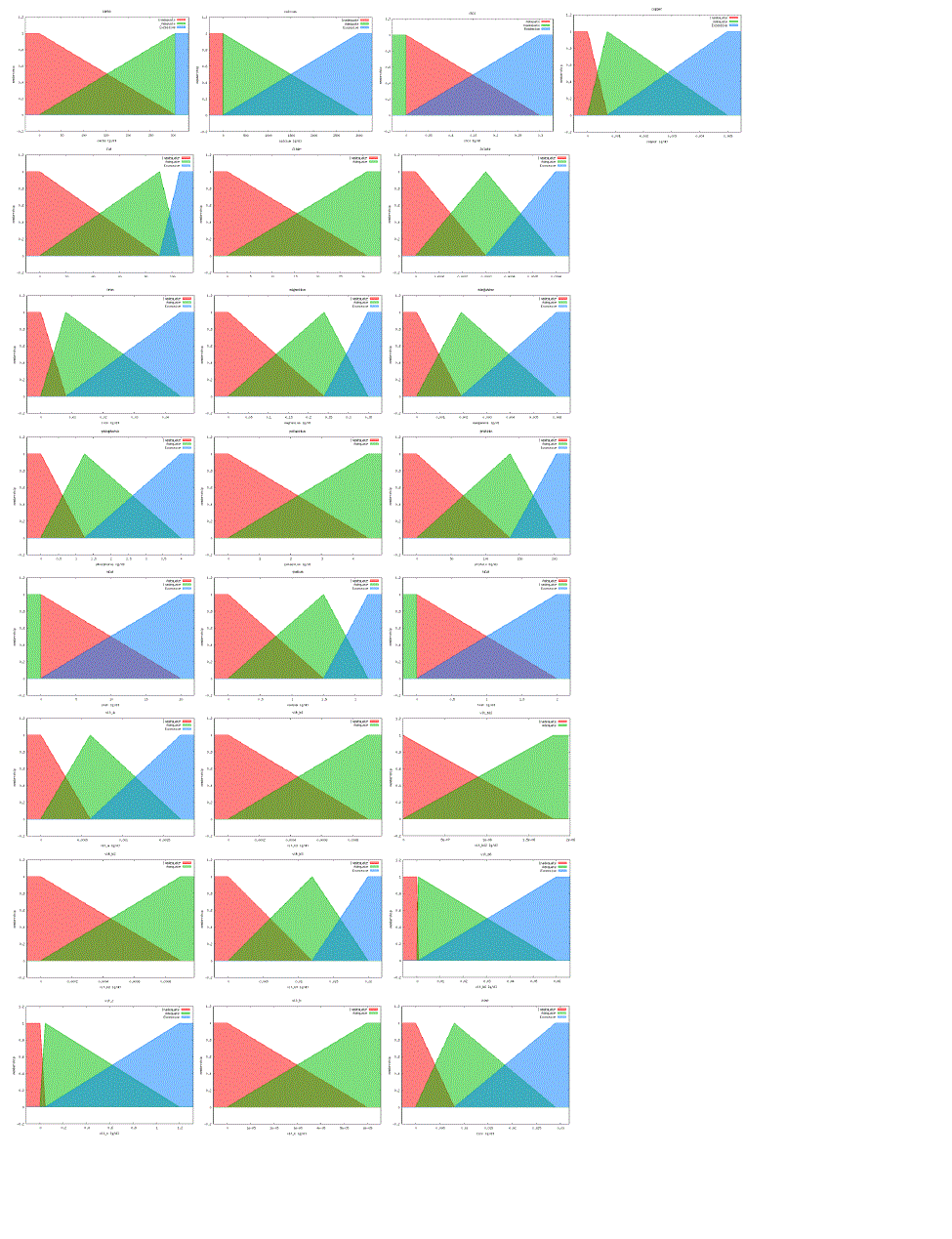
| The resulting fuzzy sets are built dynamically from the database based on the age, gender, and child rearing status of the user. As an example, Figure 3 shows the graphs representing the dietary needs of the 25 resulting nutrients for a 30 year old male. |
B. Output fuzzy sets & Fuzzy Rules
|
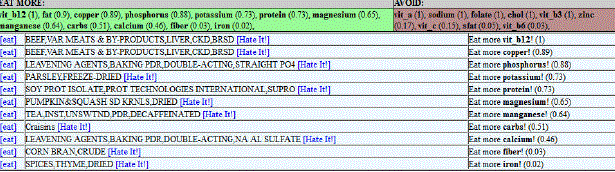
| In a typical fuzzy controller, some process is being controlled through the means of fuzzy rules. In this case, the goal is to increase the health of the user by driving them to eat more of certain nutrients and less of others. Therefore, the rules can simply map “Excessive” onto the output action “Avoid” for each nutrient, and map “Inadequate” onto an output action “Eat More”. |
C. Food Recommendation
|
1) Crisp “Clustering” Method
|
| Food recommendation can be performed using the level positioning method’s boundaries defined in [12]. This divided foods into three groups per nutrient: Less than average, average, and greater than average. Foods with a fuzzy value of “Eat More” were sought from the greater than average group for that nutrient, with an extra condition that the food must also be in the less than average group for any nutrients with a fuzzy value of “Avoid”. If a search with this criterion comes up empty, the inverse of the fuzzy value for “Avoid” is used as a weight multiplied by 10% of the range between the maximum nutrient content of the less than average group. This is performed iteratively until a food is found, and in this way the system presents the user with foods that satisfy the user’s nutrient needs, while also avoiding overconsumption of unnecessary nutrients. |
2) Fuzzy Comparison to Normal Diet
|
| Food recommendations are also determined using an entirely fuzzy method, similar to that used in [13]. The nutrients consumed are summed, and then each item in the database is added to this sum and compared to the DRI fuzzy sets, which describe a healthy diet. The comparison is made between the aggregations of the fuzzy values for each of the nutrients. An aggregation is performed by multiplying the fuzzy values by a weight that represents the importance of each nutrient and then summing up these values. The food item with the maximum value is the best recommendation. Foods are recommended iteratively until the maximum value of an iteration is less than the maximum value of the previous iteration. |
VI. SYSTEM IMPLEMENTATION
|
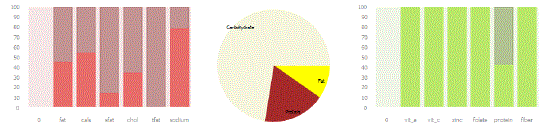
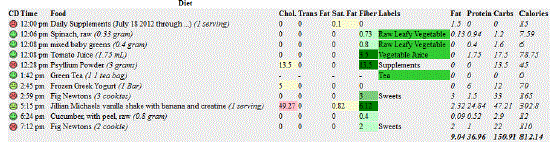
| The fuzzy system was implemented in python, based on the pyfuzzy library [30] to generate fuzzy sets and rules. The system was integrated with a web-based PHP program known as “FitterLog”, which was previously developed by the author as a diet tracking tool for his family. “FitterLog” has a database of over 1700 entered nutrition labels and a port of the USDA SR23 database, which gives the nutritional values of over 7600 food items. Figures 4 and 5 show an example of the FitterLog system without the fuzzy implementation: |
| The fuzzy system interfaces with “FitterLog” in two ways: |
| 1. Using JSON over HTTP to gather data from the system that describes the user’s age, weight, and gender. Also gathers the total nutritional values of foods consumed on that day. |
| 2. Using SQL queries for direct access to a normalized database of the USDA SR23 and custom nutritional labels databases for nutritional content for recommended foods. |
| When a user logs a food item as eaten for a given day, “FitterLog” executes the python interpreter on the fuzzy system source code, and new foods are recommended. Below is an example of the output from the fuzzy system, formatted for display in “FitterLog”: |
| The user may select the “[Hate it]” link next to a recommended food, and it will be replaced with another recommendation. A user may also select the “[eat]” link, and mark the given food as eaten. |
VII. RESULTS
|
| The pre-existing “FitterLog” tool has features for marshaling crisp data back to the user. The raw data for micronutrients from each food are accessible to the user (Fig 5) as well as the total nutrient for each day (Fig 4). Additionally, graphs representing which nutrients are necessary were tried (Fig 4). All of these data contained plentiful information that was difficult for the user to prioritize. The fuzzy system reduces the problem to “Eat More” and “Avoid” nutrients, simplifying the problem. Additionally, the fuzzy number itself is useful in prioritizing which nutrients are most needed, and also for searching for foods that contain the “Eat More” nutrients and not the “Avoid” nutrients. After using the fuzzy system for only a week, the users of “FitterLog” find dietary choices much easier than with the crisp information alone |
VIII. CONCLUSIONS & FUTURE WORK
|
| Fuzzy logic is a very convenient tool for use in nutritional analysis, but does not appear to be leveraged well in most of the past work. The current work shows simple ways in which fuzzy logic can be used to promote healthier intake of nutrients though nutritional analysis and food suggestion. Initial comparison shows it is less complicated and more intuitive to users than its crisp counterpart. |
| Future work could include adding resulting symptoms from vitamin deficiencies or excesses and implement a Type-2 fuzzy ontology system that takes into account the uncertainty of this information based on the hierarchy of evidence. Symptoms from nutrient excesses or deficiencies could operate as motivators to eat the recommended foods. It would also be pertinent to evaluate the system’s effectiveness in a suitable population study. |
Tables at a glance
|
 |
 |
| Table 1 |
Table 2 |
|
| |
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
 |
 |
 |
| Figure 5 |
Figure 6 |
Figure 7 |
|
| |
References
|
- Zadeh, LA “Fuzzy Sets”, Information and Control, vol. 8, Issue 3, June 1965, pp 338–353
- Zadeh, LA “Fuzzy Sets as a Basis for a Theory of Possibility”, Fuzzy Sets and Systems, 1978, pp 3–28
- Jepsen, T.C.; , "Just What Is an Ontology, Anyway?," IT Professional , vol.11, no.5, pp.22-27, Sept.-Oct. 2009
- Iglesias, J.; Lehmann, J.; , "Towards integrating fuzzy logic capabilities into an ontology-based Inductive Logic Programming framework,"Intelligent Systems Design and Applications (ISDA), 2011 11th International Conference on , vol., no., pp.1323-1328, 22-24 Nov. 2011
- Chang-Shing Lee; Mei-Hui Wang; Hagras, H.; , "A Type-2 Fuzzy Ontology and Its Application to Personal Diabetic-Diet Recommendation," FuzzySystems, IEEE Transactions on , vol.18, no.2, pp.374-395, April 2010
- Lee, Chang-Shing; Wang, Mei-Hui; Hsu, Chin-Yuan; Hagras, Hani; , "A Novel Type-2 Fuzzy Ontology and Its Application to Diet Assessment,"Web Intelligence and Intelligent Agent Technologies, 2009. WI-IAT '09. IEEE/WIC/ACM International Joint Conferences on , vol.3, no., pp.417-420, 15-18 Sept. 2009
- Chang-Shing Lee; Mei-Hui Wang; Zhi-Wei Chen; Chin-Yuan Hsu; Su-E Kuo; Hui-ChingKuo; Hui-Hua Cheng; Naito, A.; , "Genetic fuzzy markuplanguage for diet application," Fuzzy Systems (FUZZ), 2011 IEEE International Conference on , vol., no., pp.1791-1798, 27-30 June 2011
- Mei-Hui Wang; Chang-Shing Lee; Zhi-Wei Chen; Chi-Fang Lo; Su-E Kuo; Hui-ChingKuo; Hui-Hua Cheng; , "Property and application of fuzzyontology for dietary assessment," Fuzzy Systems (FUZZ), 2010 IEEE International Conference on , vol., no., pp.1-8, 18-23 July 2010
- Huan-Chung Li; Wei-Min Ko; , "Automated Food Ontology Construction Mechanism for Diabetes Diet Care," Machine Learning and Cybernetics,2007 International Conference on , vol.5, no., pp.2953-2958, 19-22 Aug. 2007
- Mei-Hui Wang; Chang-Shing Lee; Kuang-Liang Hsieh; Chin-Yuan Hsu; Chong-Ching Chang; , "Intelligent ontological multi-agent for healthy dietplanning," Fuzzy Systems, 2009. FUZZ-IEEE 2009. IEEE International Conference on , vol., no., pp.751-756, 20-24 Aug. 2009
- Sandham, W.A.; Hamilton, D.J.; Japp, A.; Patterson, K.; , "Neural network and neuro-fuzzy systems for improving diabetes therapy," Engineering inMedicine and Biology Society, 1998. Proceedings of the 20th Annual International Conference of the IEEE , vol.3, no., pp.1438-1441 vol.3, 29 Oct-1 Nov 1998
- Huan-Chung Li; Wei-Min Ko; Hung-Wen Tung; , "Food Clustering Analysis for Personalized Food Replacement," Fuzzy Information ProcessingSociety, 2007. NAFIPS '07. Annual Meeting of the North American , vol., no., pp.382-386, 24-27 June 2007
- Buisson, J.-C.; Garel, A.; , "Balancing meals using fuzzy arithmetic and heuristic search algorithms," Fuzzy Systems, IEEE Transactions on , vol.11,no.1, pp. 68- 78, Feb 2003
- Chengliu Li; Fernstrom, J.D.; Sclabassi, R.J.; Fernstrom, M.H.; WenyanJia; Mingui Sun; , "Food density estimation using fuzzy logic inference,"Bioengineering Conference, Proceedings of the 2010 IEEE 36th Annual Northeast , vol., no., pp.1-2, 26-28 March 2010
- B. Wirsam and E.O. Uthus, “The use of fuzzy logic in nutrition,” J. Nutrition. 1996, 126:2337S-2341S.
- Chang-Shing Lee1,*, Mei-Hui Wang1, Giovanni Acampora2, Chin-Yuan Hsu3, Hani Hagras4, “Diet assessment based on type-2 fuzzy ontology andfuzzy markup language”, Article first published online: 11 OCT 2010 DOI: 10.1002/int.20449
- Kanoni S; Nettleton JA; Hivert MF; Ye Z; van Rooij FJ; Shungin D; Sonestedt E; Ngwa JS; Wojczynski MK; Lemaitre RN; Gustafsson S; AndersonJS; Tanaka T; Hindy G; Saylor G; Renstrom F; Bennett AJ; van Duijn CM; Florez JC; Fox CS; Hofman A; Hoogeveen RC; Houston DK; Hu FB;Jacques PF; Johansson I; Lind L; Liu Y; McKeown N; Ordovas J; Pankow JS; Sijbrands EJ; Syvänen AC; Uitterlinden AG; YannakouliaM;Zillikens MC; MAGIC Investigators; Wareham NJ; Prokopenko I; Bandinelli S; Forouhi NG; Cupples LA; Loos RJ; Hallmans G; Dupuis J;Langenberg C; Ferrucci L; Kritchevsky SB; McCarthy MI; Ingelsson E; Borecki IB; Witteman JC; Orho-Melander M; Siscovick DS; MeigsJB;Franks PW; Dedoussis GV, “Total zinc intake may modify the glucose-raising effect of a zinc transporter (SLC30A8) variant: a 14-cohort metaanalysis,”Diabetes. 2011 Sep;60(9):2407-16. Epub 2011 Aug 1.
- Mitri J; Muraru MD; Pittas AG, “Vitamin D and type 2 diabetes: a systematic review,” Eur J ClinNutr. 2011 Sep;65(9):1005-15.
- Joe M. Chehade; Mae Sheikh-Ali; Arshag D. Mooradian, “The Role of Micronutrients in Managing Diabetes,” Diabetes Spectrum September 21,2009 vol. 22 no. 4 214-218
- Uusitalo U; Kronberg-Kippila C; Aronsson CA; Schakel S; Schoen S; Mattisson I; Reinivuo H; Silvis K; Sichert-Hellert W; Stevens M; Norris JM;Virtanen SM; The TEDDY Study Group, “Food composition database harmonization for between-country comparisons of nutrient data in theTEDDY Study.” J Food Compost Anal. 2011 Jun;24(4-5):494-505.
- Nettleton JA; McKeown NM; Kanoni S; Lemaitre RN; Hivert MF; Ngwa J; van Rooij FJ; Sonestedt E; Wojczynski MK; Ye Z; Tanaka T; Garcia M;Anderson JS; Follis JL; Djousse L; Mukamal K; Papoutsakis C; Mozaffarian D; Zillikens MC; Bandinelli S; Bennett AJ; Borecki IB; FeitosaMF;Ferrucci L; Forouhi NG; Groves CJ; Hallmans G; Harris T; Hofman A; Houston DK; Hu FB; Johansson I; Kritchevsky SB; Langenberg C; LaunerL; Liu Y; Loos RJ; Nalls M; Orho-Melander M; Renstrom F; Rice K; Riserus U; Rolandsson O; Rotter JI; Saylor G; Sijbrands EJ; Sjogren P; SmithA; Steingrímsdóttir L; Uitterlinden AG; Wareham NJ; Prokopenko I; Pankow JS; van Duijn CM; Florez JC; Witteman JC; MAGIC Investigators;Dupuis J; Dedoussis GV; Ordovas JM; Ingelsson E; Cupples LA; Siscovick DS; Franks PW; Meigs JB, “Interactions of dietary whole-grain intakewith fasting glucose- and insulin-related genetic loci in individuals of European descent: a meta-analysis of 14 cohort studies,” Diabetes Care. 2010Dec;33(12):2684-91. Epub 2010 Aug 6.
- Ye EQ; Chacko SA; Chou EL; Kugizaki M; Liu S, “Greater whole-grain intake is associated with lower risk of type 2 diabetes, cardiovasculardisease, and weight gain,” J Nutr. 2012 Jul;142(7):1304-13. Epub 2012 May 30.
- Post RE; Mainous AG 3rd; King DE; Simpson KN, “Dietary fiber for the treatment of type 2 diabetes mellitus: a meta-analysis,” J Am Board FamMed. 2012 Jan-Feb;25(1):16-23.
- B.A. Petrisora; J. Keatingb; E. Schemitschc, “Grading the evidence: Levels of evidence and grades of recommendation,” Injury, Volume 37, Issue 4,April 2006, Pages 321–327
- Patrick Therasse, “From clinical trials to evidence-based medicine: how to build the evidence!” EORTC Data Center, Av. E. Mounier83/11, 1200 Brussels, Belgium
- “Dietary Reference Intakes for Energy, Carbohydrate, Fiber, Fat, Fatty Acids, Cholesterol, Protein, andAmino Acids (Macronutrients)” Food andNutrition Board, 2005
- TRANSforming the Food Supply,” Trans Fat Task Force, June 2006
- “Dietary Guidelines for Americans”, U.S. Department of Health and Human Services , 2005
- R Ordman , "Dietary recommendations from the national cholesterol education program expert panel on detection, evaluation, and treatment of highblood cholesterol in adults. Unpublished manuscript". Beloit, WI: Biochemistry Program, Beloit College, 2011
- “Pyfuzzy API Documentation” 19 Oct 2009
|