GENERAL APPROACH FOR INTERNAL FAULTS
REPRESENTATION OF THREE-PHASE THREEWINDING
TRANSFORMERS IN EMTP-ATP

Mohamed A. Abd-Elaziz; Ebrahim A. Badran; Mohamed M. I. El-Shmoty

GENERAL APPROACH FOR INTERNAL FAULTS REPRESENTATION OF THREE-PHASE THREEWINDING TRANSFORMERS IN EMTP-ATP

Mohamed A. Abd-Elaziz¹, Ebrahim A. Badran², and Mohamed M. I. El-Shmoty³

Senior Electrical Engineer, Middle Delta Electricity Production Company, Talkha Power Station, Talkha, Egypt
Associate Professor, Electrical Engineering Department, Faculty of Engineering, Mansoura Univ., Mansoura, Egypt
Professor, Electrical Engineering Department, Faculty of Engineering, Mansoura Univ., Mansoura, Egypt

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Transformers are one of the most important elements in power system. Most of transformers are equipped with protection systems to avoid their damage. As the transformer outage has severed technical and economical consequences for the network, so implementing fast relaying algorithms is a challenge. Therefore, modelling of various types of internal transformer faults is the objective of this study. This paper introduces a proposed approach to model internal incipient winding faults in three-phase three-winding transformers using EMTP-ATP. The User Specified Object (USO) is used for building the transformer model under fault conditions. The proposed model have the ability to change the transformer impedance matrices in a simple manner to satisfy the internal fault conditions. The internal faults in the three-windings are simulated and tested. The results show that the proposed approach is able to represent the internal faults in the three-phase three-winding transformers accurately.

Keywords

Transformers, Three-Winding, Internal faults, EMTP-ATP, BCTRAN, User Specified Object (USO).

INTRODUCTION

Large transformers are a class of very expensive and vital components of electric power systems. Since it is very important to minimize the frequency and duration of unwanted outages, these are a high demand imposed on power transformer protective relays. Protection of large power transformers is a very challenging problem in power system relaying [1]. Since field measurements of transformer abnormal conditions, especially for internal faults, are seldom available, the information needed for the investigation of protective relays improvement may be exclusively achieved by means of digital simulation [2]. This draws a lot of attention from industry, and is now becoming widely adopted [3]. The main directions in the computer modelling for the study of the power transformer electromagnetic transients are summarized in [4]. The electrical faults of transformers are classified in two types: external and internal faults. External faults are those that occur outside of the transformer: overloads, overvoltage, over-fluxing, under frequency, and external system short circuits. Internal faults are those that occur inside of the transformer: winding phase-to-phase, phase-to-ground, winding inter-turn, over-fluxing, and etc. [6]. About 70-80% of transformer failures are caused by internal faults [7]. Several papers have introduced methods for modelling winding faults in transformers [2], [8]-[14].

The calculation of the terminal equivalent matrix of a power transformer from the standard test data is introduced in [2]. The disadvantage of the method is that the derived model for winding faults modelling of power transformer is performed only just for one simple example and with hand calculations using EMTP. A modified coupled RL matrix method which simulates the winding faults by splitting the original matrix is introduced in [8]. This method requires a detailed knowledge of the winding geometrical measures; these parameters are practically difficult to be obtained. Similarly, in [9] the leakage factor estimation is used. In [10], the complexity of the problem of leakage coefficient, derived from winding geometrical data, is simply ignored via equating it to zero. This assumption could be true for large power transformers [11], but in the smaller transformers it gives higher errors. In [12], an iterative solution is introduced using EMTP-ATP and MATLAB to estimate the parameters of the faulted transformer and the fault currents. This is achieved by solving nonlinear differential equations. This procedure suffers from the complexity during real time implementation. The aforementioned techniques, are not straightforward and the presented results didnot cover the entire range of the winding faults. Lumped RLC is used to represent the transformer winding in [13-15]. This method requires knowledge of the transformer construction details. In [14, 16], a method to establish a multisection network model for study of high frequency transient behaviour of the transformer and machine winding is presented using equally divided sections for only single winding. This makes the number of sections be large if this method is used for simulating the small turn-to-turn fault. The self and mutual impedances of the transformer are calculated directly in [17-19]. These methods have limitations because of their need for very detailed design knowledge of the transformer construction which may be not available for the old transformers.

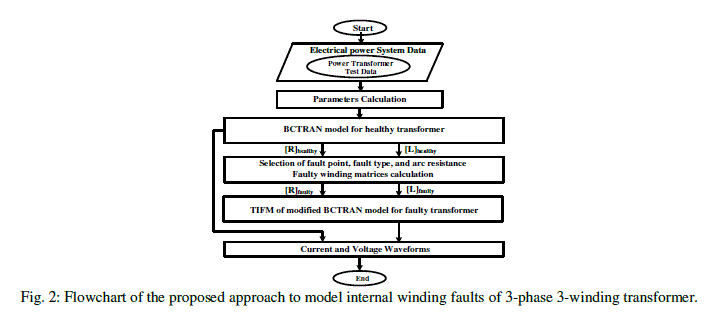
This paper introduces a proposed approach to model the internal incipient winding faults in three-phase three-winding transformers. Hence, a complete transformer model is introduced. The auxiliary routine BCTRAN in EMTP-ATP is employed to generate the healthy transformer parameters from the standard test data. Then, a direct method using the FORTRAN-capability of TACS in EMTP-ATP is used to alter and calculate the generated parameters to account the faulty transformer parameters with internal faults; turn-to-earth and turn-to-turn. This approach is directly applicable to ATPDraw of EMTP-ATP.

THE PROPOSED TRANSFORMER MODEL

The impedance matrix representation of the transformer is an important step towards realization of transformer winding faults. That is because the winding fault representation needs to modify the impedance matrix values and dimension. This undefined process is not included in the simulation programs libraries. Therefore, the modelling of transformer internal faults is discussed in this section. EMTP-ATP is used in this study using BCTRAN routine. In BCTRAN, the open circuit and short circuit tests in positive and zero sequences are used to compute elements of the two matrices; the resistance matrix [R] and the inductance matrix [L], which represents the terminal equivalent matrix of healthy transformer. More details on transformer modelling auxiliary routine could be found in [11]. The matrices are stored in a file which can be directly read by EMTP-ATP. The required parameters of the transformer tests can easily taken from the name plate and the factory test of the transformer. In case of a three-phase three-winding transformer, the matrices [R] and [L] are of order 9 as given in (1) and (2).

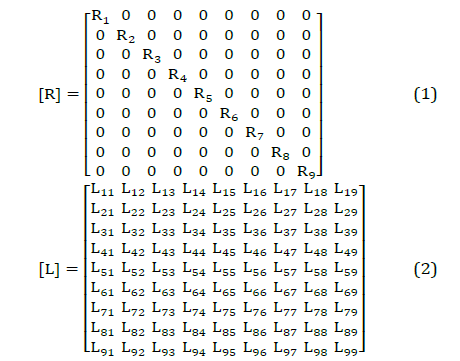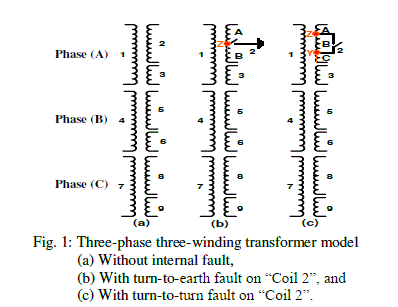
Where Ri and Lii are the resistance and self-inductance of coil i, and Lij is the mutual inductance between coils i and j, as shown in Fig. 1a.

Once [R] and [L] matrices are obtained directly for healthy transformer with a size 9x9, two types of winding faults are considered: turn-to-earth fault and turn-to-turn fault. The basic idea of modelling faults is to modify the size of [R] and [L] matrices to a size of 10x10 for turn-to-ground faults and a size of 11x11 for turn-to-turn faults. Therefore, based on the leakage impedance method which presented in the equations of [8] and [11], a FORTRAN capability of TACS is used to prepare the modified parameters of the modified matrices. These modified parameters are varied depending on the location of the fault points and if the other mutual coupled coil in for each case is wound on different leg or on the same leg with faulty coil. A simplified flowchart of the proposed approach is shown in Fig. 2. The results of numerical case studies show that the proposed approach to model internal winding faults of transformers are found satisfactory and applicable for protective relaying studies.

A. Turn-to-Ground Internal Fault

In order to model the transformer with an internal fault from a winding to the ground, the faulty coil is divided into two sub-windings; A and B. Therefore; the modified resistance and inductance matrices; [R'] and [L'], of the transformer which represent one point of the internal fault to the ground will be of order 10. The modified impedance matrix accommodates the fault point Z. The fault can then represented by closing a simple time controlled switch between the fault point Z and the ground at the fault instance. Furthermore, the fault resistance, or the fault arc resistance, can be added in a simple manner to the faulty path.

The simulation of the transformer turn-to-ground fault on the low voltage side of phase A at Coil 2 is illustrated in Fig.1b. The new 10x10 modified [R'] and [L'] matrices which represent this fault case are given in (3) and (4). It can be shown the highlighted elements with the italic font are the new elements that easily and directly obtained from the computer FORTRAN program which solve the equations in [8] and [11]. A new user specified object in ATPDraw is used to create the proposed transformer modified model; Transformer Internal Fault Model (TIFM), which contains the modified transformer matrices. TIFM is designed to get the required faulted coil, the fault position, and the fault resistance. The required modified matrices are calculated with very fast and accurate solutions and replaced by the healthy transformer matrices. Because if a little error exists in the calculation or entering the values to the (TIFM), will cause the unstable simulation or different waveform on pre-fault condition.

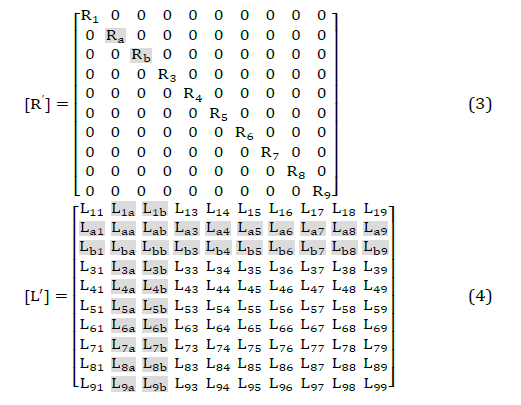B. Turn-to-Turn Internal Fault

The transformer turn-to-turn fault is represented using a similar way as turn-to-ground fault, except that the winding is divided to three parts; A, B, and C. The modified resistance and inductance matrices; [R''] and [L''], of the transformer which represent one point to another point internal fault will be of order 11. The modified impedance matrix accommodates the fault points Z and Y. The fault can then represented by closing a simple time controlled switch between the faulty points at the fault instance. Furthermore, the fault arc resistance can be added in a simple manner to the faulty path.

The simulation of the transformer turn-to-turn fault on the low voltage side of phase A at Coil 2 is illustrated in Fig.1c. The new 11x11 modified [R''] and [L''] matrices which represent this fault case are given in (5) and (6). It can be shown the highlighted new elements in the matrices. Furthermore, the winding turn-to-turn including earth fault current is simulated using a similar way by adding another time controlled switch between one of the two faulty points and the ground at the fault instance. TIFM design is modified to get the required fault type in addition to the other data such as the fault coil, the fault position, and the fault resistance. The required modified matrices are calculated and replaced by the healthy transformer matrices.

THE PROPOSED MODEL VERIFICATION

The first step for the proposed model verification is to model the healthy power transformer using BCTRAN in ATP. BCTRAN data are obtained from the short circuit and the open-circuit tests of the power transformer. The methodology of data calculation is introduced in [20-22]. The test power system under study consists of a 150 kV, 50 Hz, threephase source feeding a dynamic RL load through a three-phase three-winding, 100 MVA, 150/70/16 kV, Υ/Υ/Δ, power transformer [23]. Fig. 3 illustrates the test system model in ATPDraw.

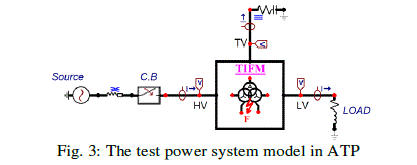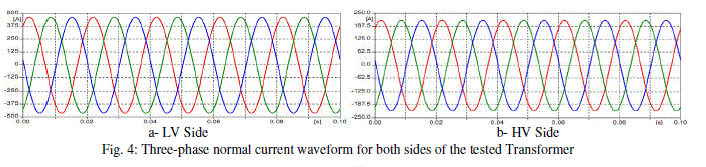
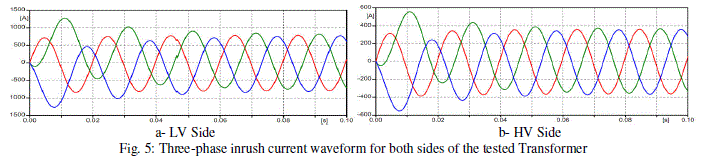
The tertiary winding of the transformer is unloaded. In order to avoid matrix singularity, 0.005 μF stray capacitances of the tertiary terminals are added for simulation purposes. The normal operation current waveforms are shown in Fig. 4 for both the high voltage (HV) and the low voltage (LV) terminals. Furthermore, the inrush current cases are successfully recorded. Fig. 5 illustrates the inrush current waveforms for both the HV and the LV terminals.

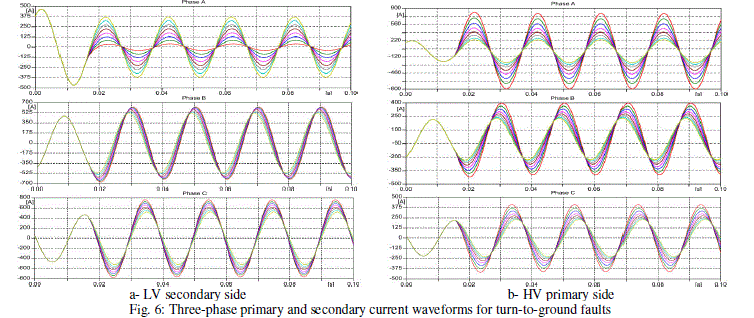
The second step for the proposed model verification is to represent the faulty winding of the transformer. A turn to earth fault is applied on phase A of the LV (secondary) side of coil 2 at 0.015 sec. The fault is applied at 10%, 20% 30%, 40%, 50%, 60%, 70%, or 80% of the winding. Fig. 6 illustrates a comparison between the three-phase currents of the LV (secondary) side and HV (primary) side for phase A, phase B, and phase C during the fault scenarios.

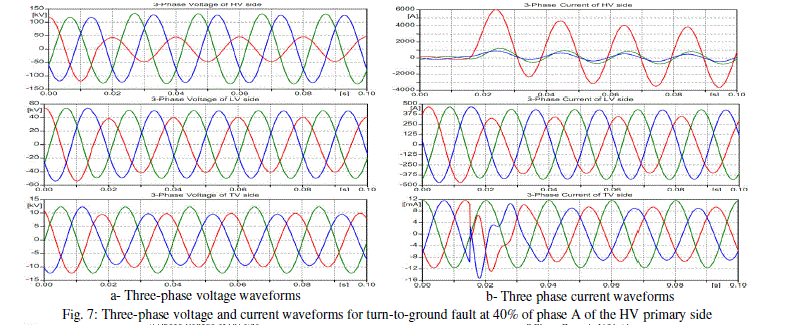
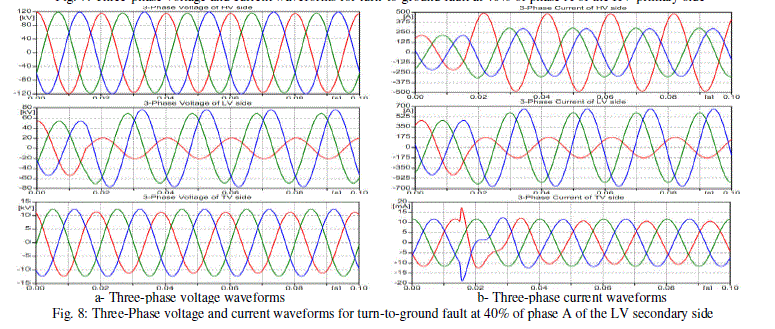
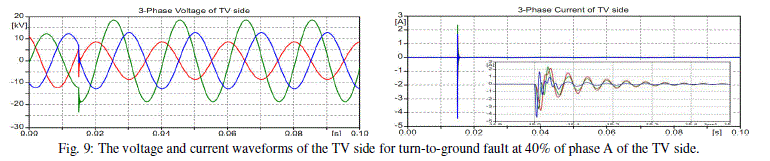
In the proposed model, the tertiary winding (TV) is also affected by the fault in any other winding, and the current is so small nearly in (mA) values in normal cases and reach small values of amperes in faulty cases, so that the ordinary protection systems are not enough to sense these values and the methods to implement new protection techniques for power transformers are necessary. Fig. 7 illustrates the three-phase current and voltage waveforms for the windings of HV, LV, and TV sides for turn-to-ground fault at 40% of phase A of the HV side at 0.015 sec. The same effect can be verified if the fault is applied on the LV side at 40% of phase A at 0.015 sec., as shown in Fig. 8. Furthermore, Fig. 9 illustrates the voltage and current waveforms if the fault is applied at 40% of phase A of the TV side at 0.015 sec. In this case, there is no significant current difference between pre-fault and fault condition for the primary and secondary current waveforms and there are significant changes in the voltages of HV, LV, and TV sides.

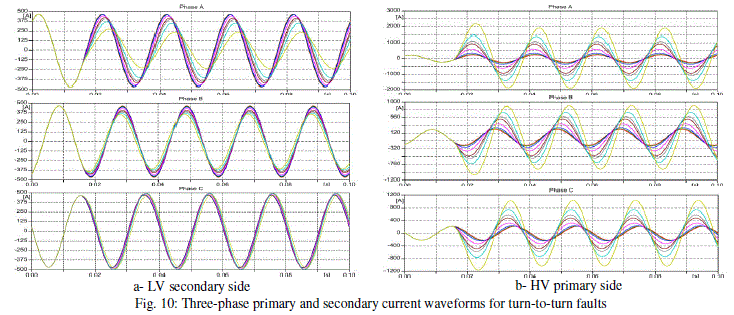
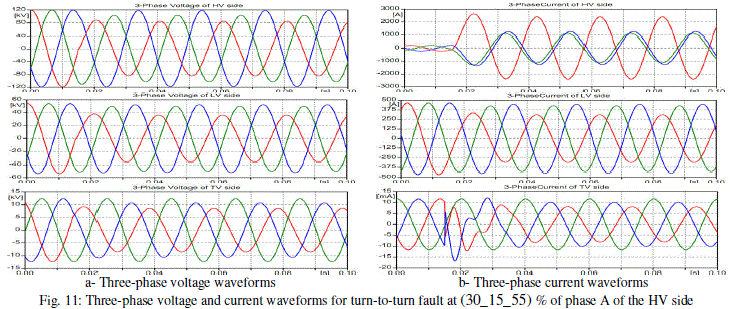
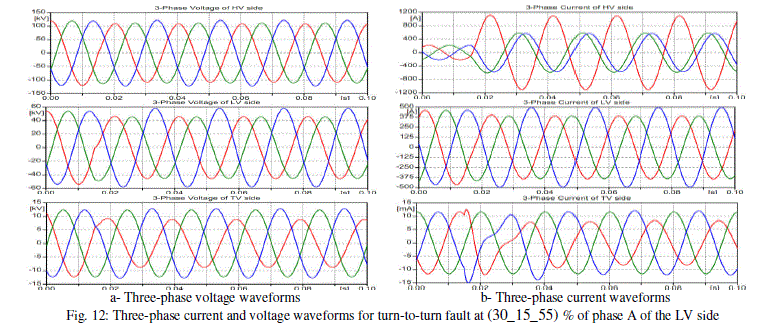
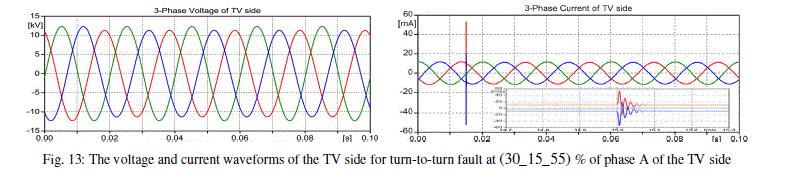
Also, a turn to turn fault is applied to phase A of the LV (secondary) side of coil 2 at 0.015 sec. The fault is applied at 8 different and optional locations of the winding. Fig. 10 illustrates a comparison between the three-phase currents of the LV (secondary) side and HV (primary) side for phase A, phase B, and phase C during the fault scenarios. Fig. 11 illustrates the three-phase current and voltage waveforms for the windings of HV, LV, and TV sides for turn-to-turn fault at (30_15_55) % of phase A of the HV side at 0.015 sec. The same effect can be verified if the fault is applied on the LV side at (30_15_55) % of phase A at 0.015 sec., as shown in Fig. 12. Furthermore, Fig. 13 illustrates the voltage and current waveforms if the fault is applied at (30_15_55) % of phase A of the TV side at 0.015 sec. In this case, there is no significant current difference between pre-fault and fault condition for the primary and secondary current waveforms and there are significant changes in the voltages of HV, LV, and TV sides.

From the study of various fault scenarios discussed above it can be seen that the proposed approach have the ability to represent the internal faults in the transformer windings. The response of all the faults applied on any point in the three-winding are clearly appear in all of the three-winding terminals. Therefore, the proposed model can be used for protection studies in EMTP-ATP to change the transformer parameters during the study in a simple way.

CONCLUSION

This paper presents a complete model for the internal incipient winding faults in the three-phase three-winding transformers. The auxiliary routine BCTRAN in EMTP-ATP is employed to generate the healthy power transformer parameters from the standard test data. Then, a direct method using the FORTRAN-capability of TACS in EMTP-ATP is used to alter and calculate the generated parameters to account the faulty transformer impedance matrices with internal faults; turn-to-earth and turn-to-turn. This method is directly applicable to ATPDraw of EMTP-ATP.

The proposed approach represents a modified transformer model by coupled-RL coils and adds an internal fault by subdividing the winding into sub-coils and calculates the new parameters. The position of the internal fault points which simply implemented by using the proposed approach is optionally selected by the user. The proposed approach uses the available data from the transformer standard tests and it can be used as an add-on with ATPDraw or in conjunction with advanced modelling and testing tools for short-circuit related activities such as protective relay setting, testing, evaluating and enhancing. The simulated results clearly show that the proposed TIFM model is accepted.

References

Mao P. L., and Aggarwal R. K., “A Novel Approach to the Classification of the Transient Phenomena in Power Transformers Using Combined Wavelet Transform and Neural Network”, IEEE Transactions on Power Delivery, Vol. 16, No. 4, pp. 654–660, 2001.
Darwish H. A., Taalab A. M. I., and Labana H. E., “Step-by-Step Simulation of Transformer Winding Faults for Electromagnetic Transient Programs”, Transmission and Distribution Conference and Exhibition 2005/2006, IEEE-PES, pp. 177-180, 2006.
Kezunovic M., and Chen Q., “A Novel Approach for Interactive Protection System Simulation”, IEEE Transactions on Power Delivery, Vol. 12, No. 2, pp. 668–674, 1997.
León F., and Semlyen A., “Complete Transformer Model for Electro-Magnetic Transients”, IEEE Transactions on Power Delivery, Vol. 9, No. 1, pp.231–239, 1994.
Kezunovic M., Kasztenny B., Galijasevic Z., and Williams D., “A New ATP Add-On for Modeling Internal Faults in Power Transformers”, American Power Conference, Chicago, pp. 1-5, 2000.
IEEE Std C37.91-2000, “IEEE Guide for Protective Relay Applications to Power Transformers”.
Barzegaran M. R., and Mirzaie M., “Detecting the Position of Winding Short Circuit Faults in Transformer Using High Frequency Analysis”, European Journal of Scientific Research, Vol. 23, pp. 644-658, 2008.
Bastard P., Bertrand P., and Meunier M., “A Transformer Model for Winding Fault Studies”, IEEE Transactions on Power Delivery, Vol. 9, No.2, pp.690-699, 1994.
Wang H., and Butler K L., “Modeling Transformer with Internal Winding Faults by Calculating Leakage Factors”, Proceedings of the 31st North American Power Symposium, San Luis Obispo, CA, pp. 176–182, 1999.
Palmer-Buckle P., Butler K., and Sarmaand Alvin Kopp N. D. R., “Simulation of Incipient Transformer Faults”, Proceedings of 1998 Midwest Symposium on Circuits and Systems, Notre Dame, IN, pp. 50-53, 1998.
Brandwajn V., Dommel H. W., and Dommel I. I., “Matrix Representation of Three-Phase N-Winding Transformers for Steady-State and Transient Studies”, IEEE Transaction on Power Apparatus and Systems, Vol. PAS-101, No. 6, pp.1369-1378, 1982.
Kezunovic M. and Guo Y., “Modeling and Simulation of the Power Transformer Faults and Related Protective Relay Behavior”, IEEE Transaction on Power Delivery, Vol. 15, No. 1, pp. 44-50, 2000.
Degeneff R. C., Gutierrez M. R., and Mckenny P. J., “A Method for Constructing Reduced Order Transformer Models for System Studies from Detailed Lumped Parameter Models”, IEEE Transaction on Power Delivery, Vol.7, No. 2, pp. 649–655, 1992.
Chimklai S., and Marti J. R., “Simplified Three-Phase Transformer Model for Electromagnetic Transient Studies”, IEEE Transaction on Power Delivery, Vol. 10, No. 3, pp. 1316–1325, 1995.
Noda T., Nakamoto H., and Yokoyama S., “Accurate Modeling of Core-Type Distribution Transformers for Electromagnetic Transient Studies”, IEEE Transactions on Power Delivery, Vol. 17, No. 4, pp. 969-976, 2002.
Keyhani A., Tsai H., and Abur A., “Maximum Likelihood Estimation of High Frequency Machine and Transformer Winding Parameters,” IEEE Transactions on Power Delivery, Vol. 5, No. 1, pp. 212–219, 1990.
Wilcox D. J., Conlon M., and Hurley W. G., “Calculation of Self and Mutual Impedances between Sections of Transformer Windings”, IEEE Proceedings, Vol. 136, Pt-C, No. 5, pp. 308-314, 1989.
Reynders J., “The Prediction of Fault Currents in a Large Multi-winding Reactor Transformer”, IEEE Power Tech Conference, pp. 1-5, 2003.
León F., and Semlyen A., “Efficient Calculation of Elementary Parameters of Transformers”, IEEE Transactions on Power Delivery, Vol. 7, No. 1, pp. 376–383, 1994.
“Alternative Transient Program (ATP) Rule Book”, 1996.
“Electromagnetic Transient Program (EMTP) Theory Book”, 1986.
Prikler L., Høidalen H. K., “ATPDraw version 5.6 for Windows Users' Manual”. SINTEF Energy Research, Norway, November 2009.
Popov M., Smit J. J., Bauer P., and Dakhlan D. F., “Modeling of Internal Faults in Three-phase Three-Winding Transformers for Differential Protection Studies”, Delft University of Technology, 2009.