ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Virendra Nayak1, Y.P. Banjare2, M. F. Qureshi3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
A soft computing technique based on the combination of Multiple Adaptive Neuro-Fuzzy Inference System (M-ANFIS) and a Genetic Algorithm (GA) has been developed for the discovery and optimization of new materials when exploring a high-dimensional space. This technique allows the experimental design in the search of new solid materials with high catalytic performance when exploring simultaneously a large number of variables such as elemental composition, manufacture procedure variables, etc. This integrated architecture (M-ANFIS+GA) allows one to strongly increase the convergence performance when compared with the performance of conventional GAs. It is described how both soft-computing techniques are built to work together. The proposed optimization architecture has been validated using two hypothetical functions, based on the modeled behavior of multi-component catalysts explored in the field of combinatorial catalysis. The method consists of following stages. First, prior to feature extraction, some preprocessing techniques, Secondly, the six salient feature sets are input into the multiple ANFIS combination with genetic algorithms (GAs) for discovery and optimization of new materials. The proposed method is applied for discovery and optimization of new materials and testing results show that the multiple ANFIS combination can reliably recognize, discover and optimize new materials, which has a better performance compared to the individual GA based on ANFIS.
INTRODUCTION |
| Optimization of a multiple output system, whose function is only approximately known and is represented in tabular form, is modeled and optimized by the combined use of a neuro-fuzzy network and optimization techniques which do not require the explicit representation of the function. Neuro-fuzzy network is useful for learning the approximate original tabular system. However, the results obtained by the neuro-fuzzy network are represented implicitly in the network. The M-ANFIS neuro-fuzzy network, which is an extension of the ANFIS network.the multiple output system and a genetic algorithm is used to optimize the resulting multiple objective decision making problem. |
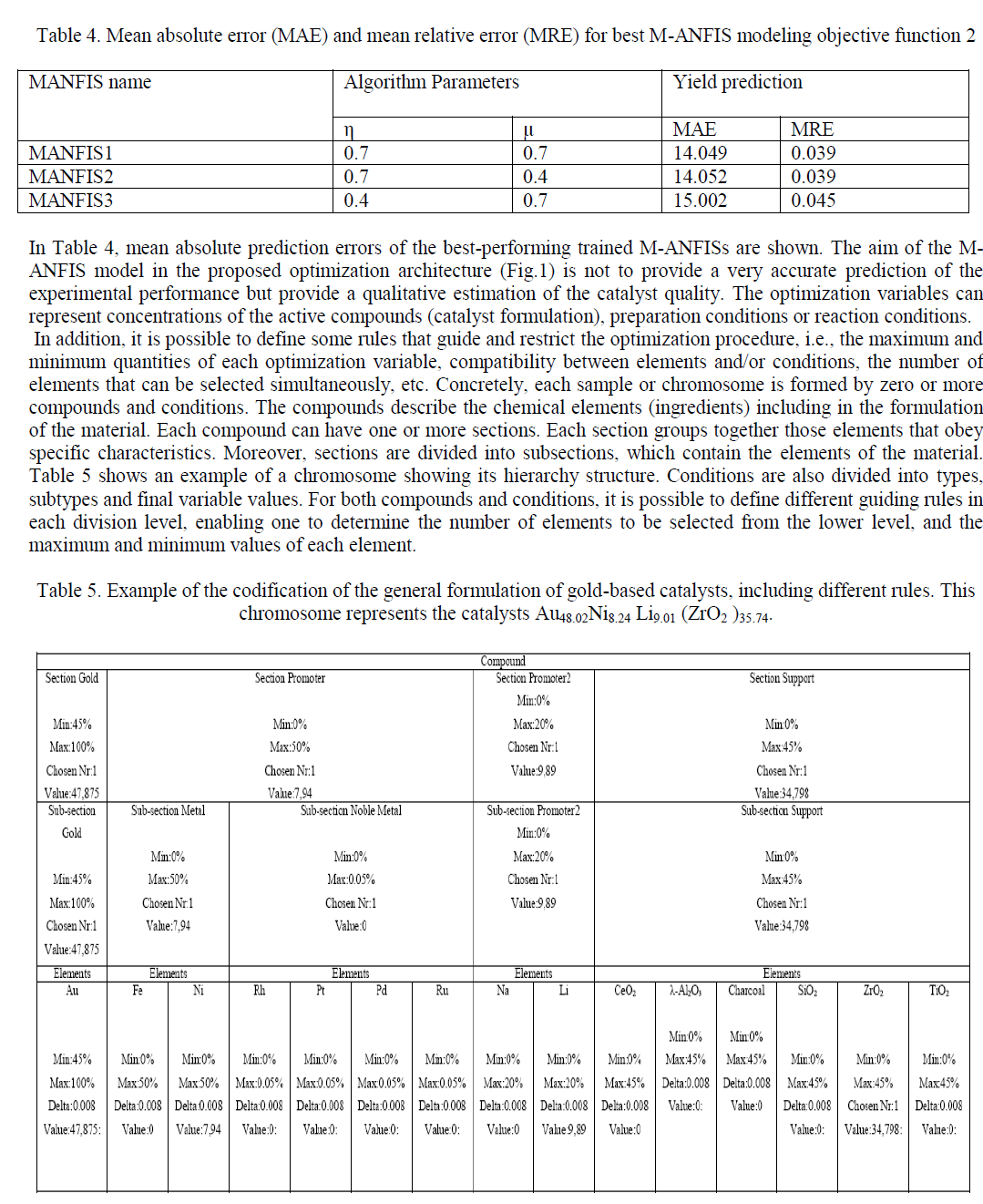
| Research in catalysis that applies accelerated experimental tools combined with powerful computational techniques constitutes what is called combinatorial catalysis. An important issue in combinatorial catalysis is how to design the experiments in order to explore and optimize the high-dimensional solution space while minimizing the number of trials to achieve a solution. The approach employed for experimental design is stochastic procedures like simulated annealing or Genetic Algorithms (GAs). An important issue in combinatorial science is the analysis and mining of the raw multi-dimensional experimental data (Kim etal. 1998), in such a way that knowledge can be systematically extracted and used to establish multi-factor relationships and patterns amongst input variables (catalyst composition, preparation and reaction conditions), output variables (catalyst characterization and catalytic performance) and also theoretical parameters concerning the catalyst components (electro-negativities, ionization energies, enthalpies of formation, etc.). Several data-mining techniques have been applied in combinatorial chemistry; examples include clustering models and non-linear regression models, statistical models, association rules and decision trees, rule induction, Kohonen and Artificial Neural Networks (ANNs). ANNs have been applied successfully in modeling catalytic systems; especially interesting here is their application in modeling complex multi-dimensional data derived from HT experimentation (Ortiz etal 2001). A promising novel approach (Khuri etal 1981) is the combination of powerful data-mining tools with high-dimensional optimization algorithms, in such a way that the knowledge extracted from all the previous experimentation can be applied in the design of the new subset of catalysts to be experimentally screened in the next optimization step. In the present work, we described a new optimization procedure employing a combination (hybrid) of a Multiple ANFIS (M-ANFIS) and a genetic algorithm (GA). Hence, the Multiple ANFIS finds the internal relationships between catalyst variables in the data from the screening of the previous generations, and the optimization algorithm (GA) designs the next generation of catalysts to be screened taking into account the knowledge extracted from the Multiple ANFIS model. |
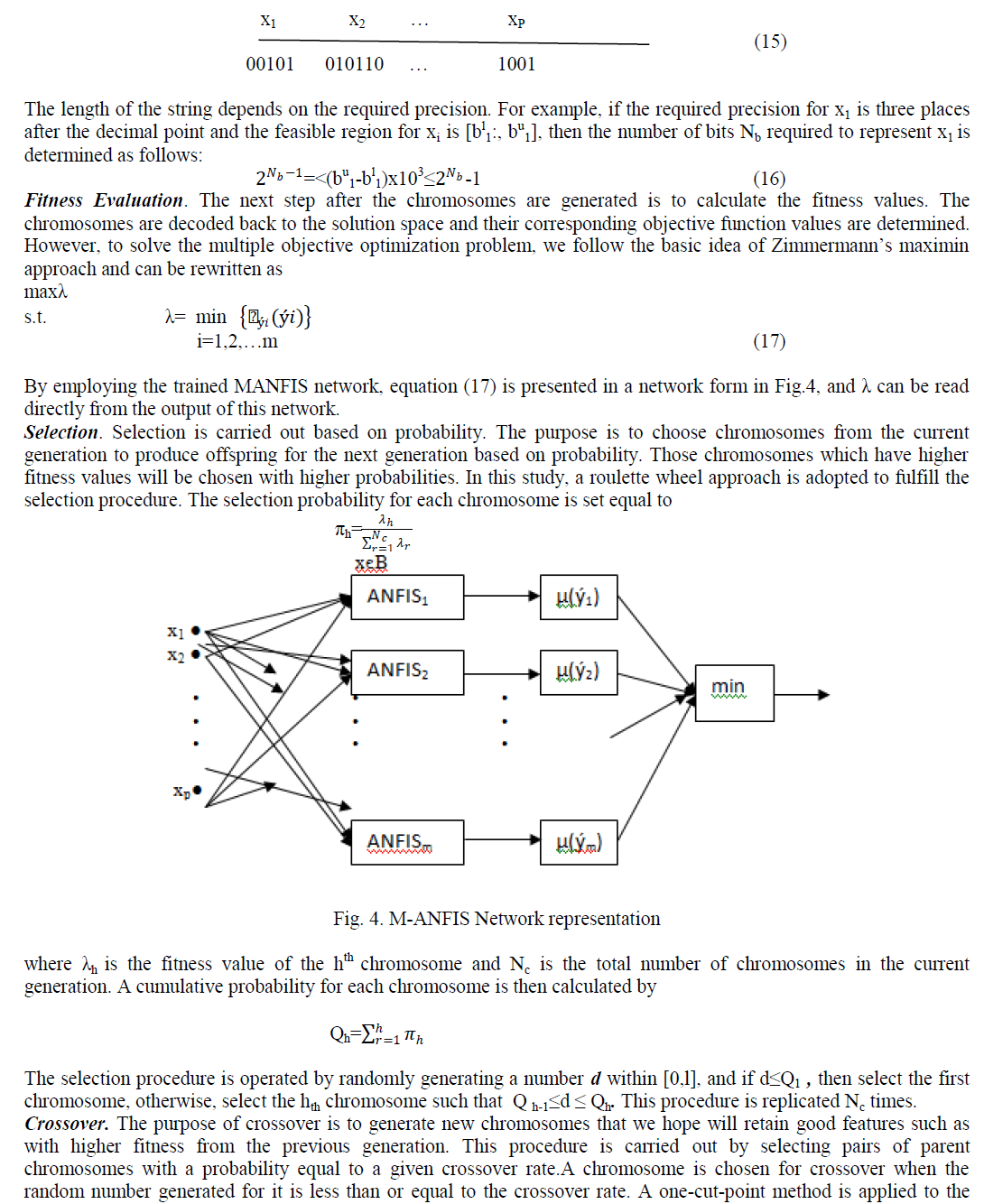
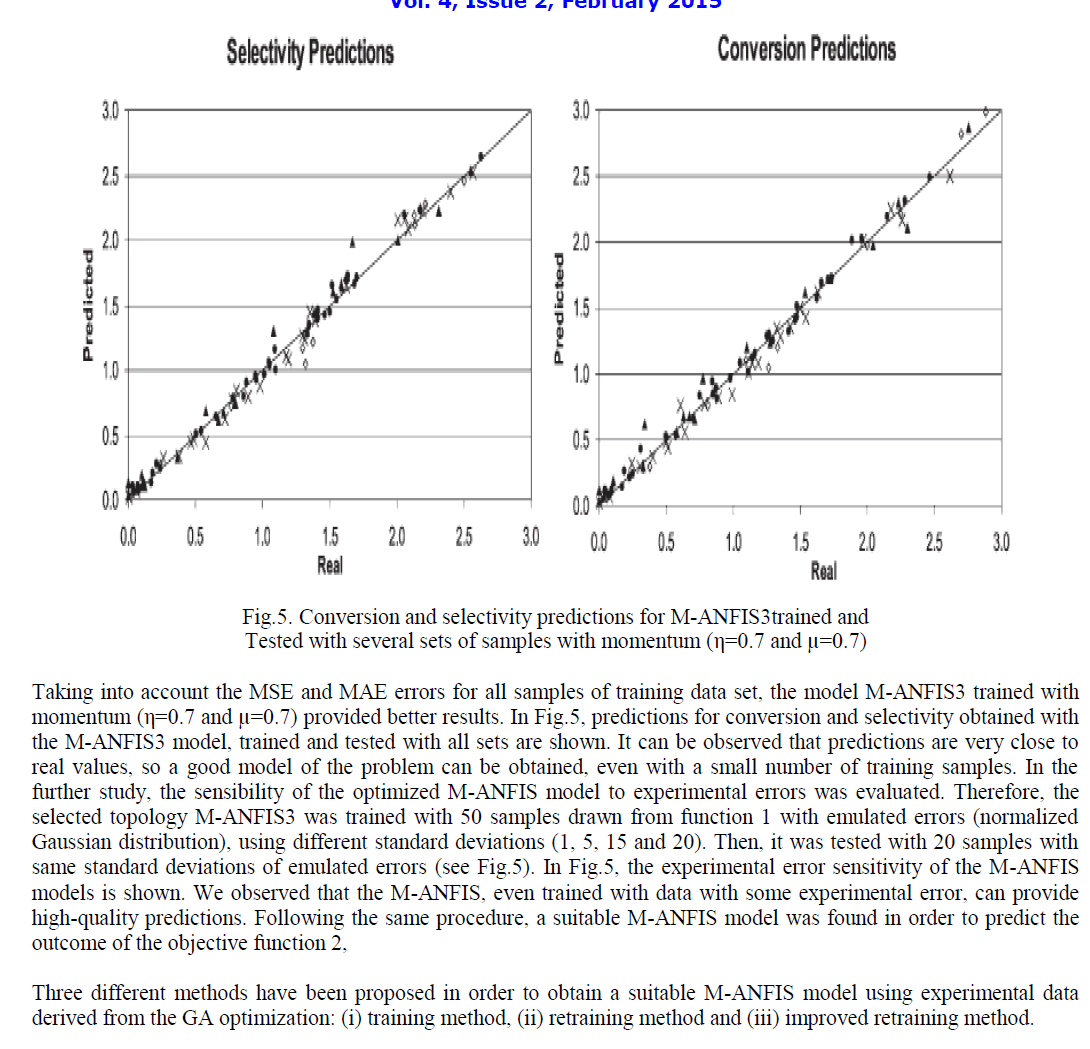
| Multiple response optimization deals with systems that have more than one response. However, since many practical systems are complicated and highly nonlinear, and thus, linear regression is not suitable, we shall adopt a much more powerful neuro-fuzzy approach, namely, the multiple adaptive neuro-fuzzy inference system (M-ANFIS), to model the system responses. M-ANFIS is a generalization of the neuro-fuzzy system ANFIS (Serra etal 2004) to handle multiple outputs or multiple responses. A neuro-fuzzy system is a nonparametric regression tool, which models the regression relationship nonparametrically without reference to any prespecified functional form, and it is capable of modeling highly nonlinear and approximately known systems. Many approaches have been proposed to solve the multiple response optimization problems. Furthermore, since the functional form of the model is unknown, optimization methods, which require the explicit expression of the functional form cannot be directly applied. In this work, a genetic algorithm (GA) is employed to search the optimal solution on the response surfaces modeled by M-ANFIS. In the next section, the architecture of M-ANFIS and its learning process are summarized. The formulation of the multiple response optimization problems is presented and the genetic algorithm is used to search for the optimal solution. |
| The adaptive neuro-fuzzy inference system (ANFIS) is a hybrid model which combines the ANNs adaptive capability and the fuzzy logic qualitative approach (Ortiz etal 2001). ANFIS harnesses the power of the two paradigms: ANNs and fuzzy logic, and overcomes their own shortcomings simultaneously. Recently the combination of Multiple ANFIS has been intensively studied to overcome the limitations of individual ANFIS and achieve higher performance (Ortiz etal 2001). Multiple ANFIS differing in feature set usually exhibit complementary optimization behavior. Thus, if the optimization results of Multiple ANFIS, which employ the same optimization engine but different input feature sets, are combined by integration techniques to yield the final optimization result, the final performance may be superior to the best performance of a single ANFIS on one feature set (Ames etal 1981). The weighted averaging technique is the simplest and most widely used technique combining Multiple ANFIS, which assigns a nonnegative weight to each individual ANFIS. By optimizing an objective function, the Multiple ANFIS weights can be estimated using various techniques. The weighted averaging technique with GAs is employed to combine the outputs of the six ANFISs and come up with the final optimization results. The proposed method is applied for Discovery and Optimization of Catalytic Materials and a desired result has been obtained adopting the combination of multiple ANFISs via Gas |
SOFT COMPUTING ALGORITHM-PROPOSED ARCHITECTURE AND IT’S WORKING |
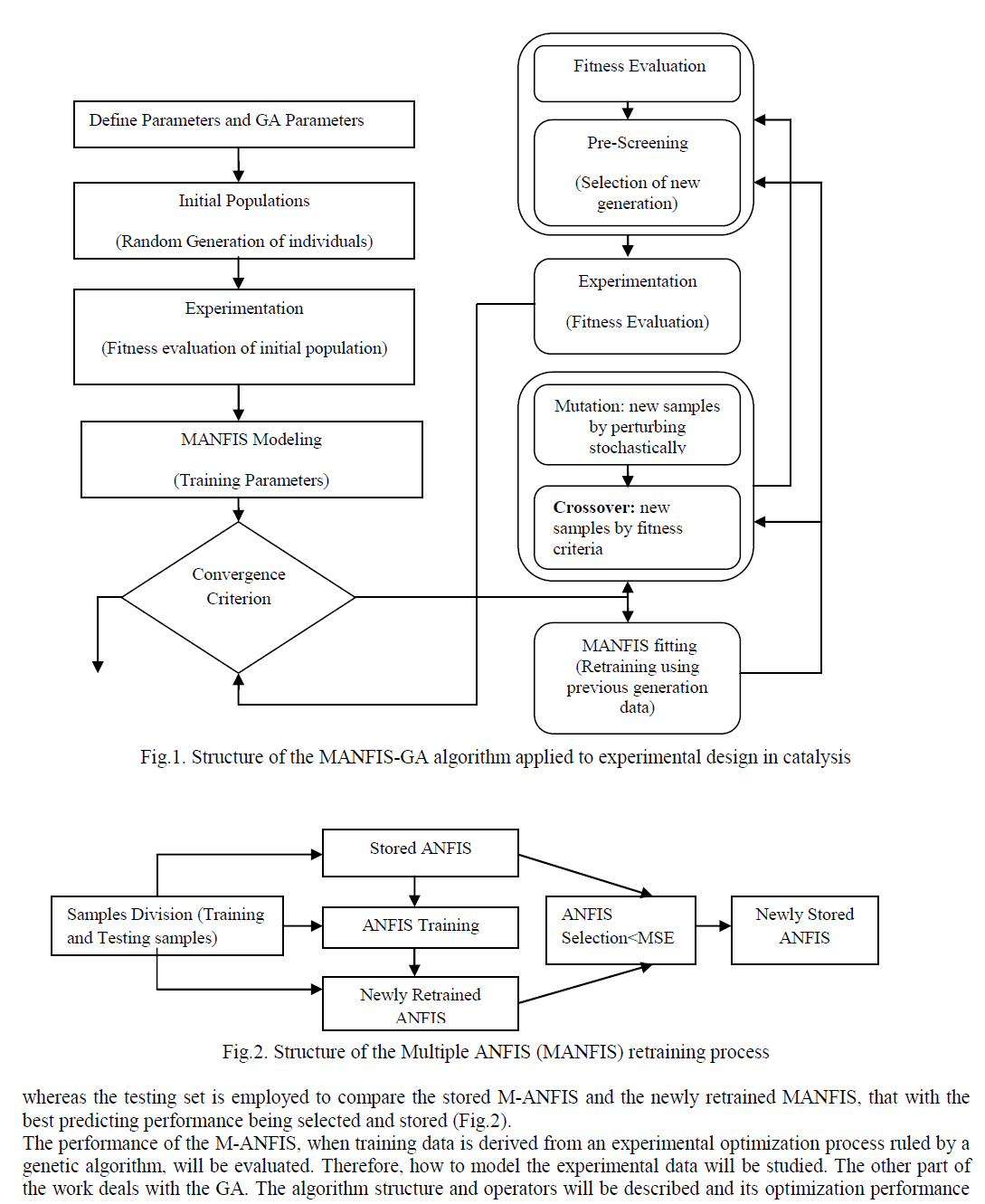
| In this work, a new optimization architecture based on combination of a M-ANFIS and a genetic algorithm (soft computing technique) will be described, this technique being specially suited for the discovery and optimization of catalytic materials, when exploring a high-dimensional space (Fig.1). In the setting-up process, the optimization variables of the material are defined considering the state of the art. Afterwards, the GA parameters are established. Moreover, an initial set of materials is obtained following a process that guarantees population diversity. This process consists of creating several random generations and carrying out a statistical population study in order to select the most diverse population. |
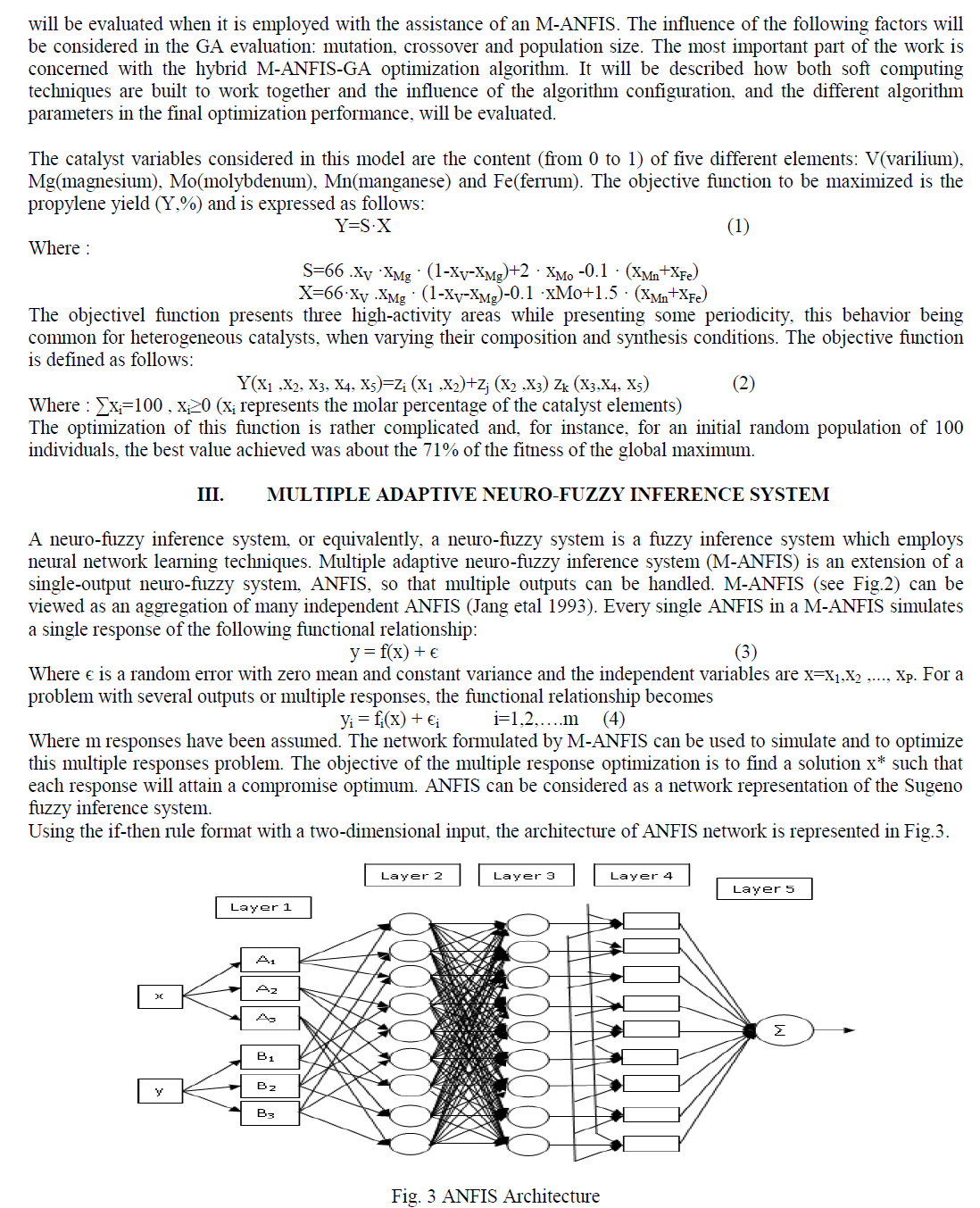
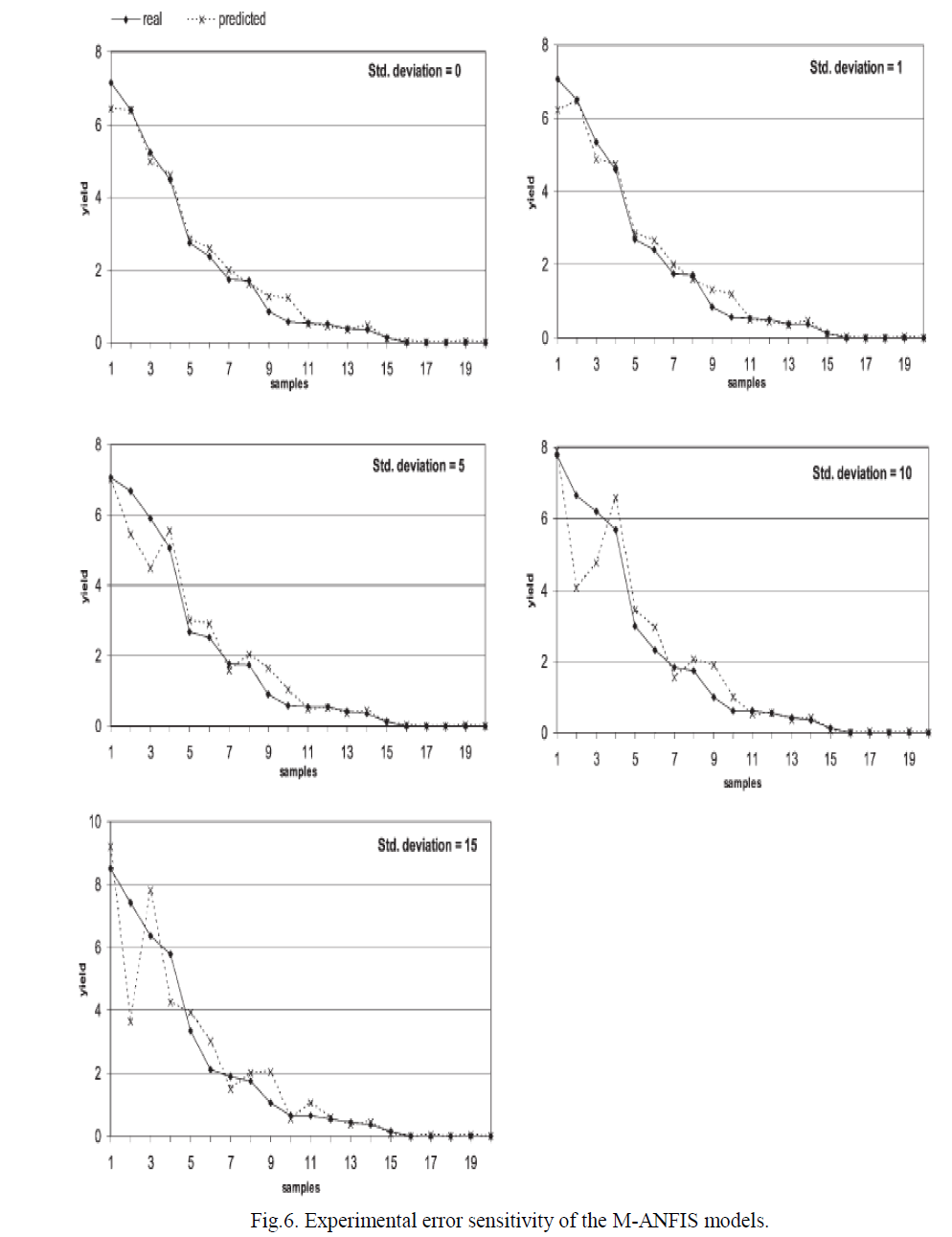
| Furthermore, the selected initial population is tested experimentally and these experimental data are subsequently used in M-ANFIS modeling, where different ANFISs and several training algorithms are tested. As a result of this study, a suitable M-ANFIS model is selected for predicting the catalytic performance. Regarding the M-ANFIS retraining step, new experimental data derived from the testing of each succeeding generation is divided into training and testing data. The training set is used to re-train the stored M-ANFIS, |
 |
 |
 |
 |
 |
 |
 |
 |
 |
CONCLUSIONS |
| This new optimization architecture for the intelligent discovery of new catalytic materials integrates an M-ANFIS and a genetic algorithm, being the integration/interaction between both very strong. Therefore, this approach is especially appropriate for high dimensional optimization (GA) while keeping in memory (M-ANFIS) the whole history of the search, reducing the experimental screening of statistically poor active materials. This integrated architecture allows one to increase strongly the convergence performance when compared with the performance of conventional genetic algorithms. The genetic algorithms and artificial neural networks are fully integrated for the design of experiments in the field of combinatorial catalysis, following the concepts already stated in Ortiz etal 2001.In this paper, we proposed the combined use of a neuro-fuzzy learning network, namely, the M-ANFIS network, and a derivative free optimization technique, namely, the genetic algorithm, to model and to solve a multiple nonlinear response system. The neuro-fuzzy network replaces the modeling or the usually used regression techniques, which cannot handle complicated nonlinear and approximately known systems. Since the results are implicitly represented by the M-ANFIS and the explicit functional form is unknown, some optimization approaches which does not require the explicit representation of the model must be used. Genetic algorithm is an ideal approach to serve this purpose. |
References |
|