Research and Reviews - International Journals

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Implementation of Efficient Modified Booth Recoder for Fused Sum-Product Operator

A.Sindhu1, K.PriyaMeenakshi2
  1. PG Student [VLSI], Dept. of ECE, Muthayammal Engineering College, Rasipuram, Tamil Nadu, India
  2. Assistant Professor, Dept. of ECE, Muthayammal Engineering College, Rasipuram, Tamil Nadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Digital signal processing (DSP) is widely used in many applications. The ability of distributed arithmetic is to reduce a multiply operation into a series of shifts and additions yields great potential for implementing various DSP systems at a significantly reduced area. However, this reduction in area comes at the cost of increased power and decreased throughput. To overcome this problem Modified booth algorithm can be used to reduce critical delay, power consumption. To increase a performance Fused add multiply operator can be used to obtain a high throughput.

Keywords
Modified Booth algorithm, Reduced area, Throughput

INTRODUCTION
Booth recoding is widely used to reduce the number of partial products in multipliers . The benefit is mainly an area reduction in multipliers with medium to large operand widths (8 or 16 bits and higher) due to the massively smaller adder tree, while delays remain roughly in the same range.Different recodings exist resulting in different gatelevel implementations and performance. In this work the XOR-based implementation gives lowest area and delay numbers in most technologies due to the small selector size and the well-balanced signal paths.An implementation of a radix-4 butterfly has been developed. The number of stages has been reduced. This reduction comes from the fact that, to achieve a throughput comparable to that of radix-2. Therefore, the implementation of the radix-4 butterfly is suitable for high speed applications, since the hardware cost, the power consumption and the latency are reduced. To reduce the number of calculation steps for the partial products, MBA algorithm has been applied mostly where Wallace tree has taken the role of increasing the speed to add the partial products.

II. RELATED WORK
Recent research activities in the field of arithmetic optimization have shown that the design of arithmetic components combining operations which share data, can lead to significant performance improvements. Based on the observation that an addition can often be subsequent to a multiplication (e.g., in symmetric FIR filters). Most digital signal processing methods use nonlinear functions such as discrete cosine transform (DCT) or discrete wavelet transform(DWT). Because they are basically accomplished by repetitive application of multiplication and addition, the speed of the multiplication and addition arithmetic’s determines the execution speed proceedings and performance of the entire calculation. Because the multiplier requires the longest delay among the basic operational blocks in digital system, the critical path is determined by the multiplier, in general. For high-speed multiplication, the modified radix-4 Booth’s algorithm (MBA) is commonly used. A signed-bit MB recoder which transforms redundant binary inputs to their MB recoding form. A special expansion of the preprocessing step of the recoder is needed in order to handle operands in carry-save representation . proposes a two-stage recoder which converts a number in carry-save form to its MB representation. The first stage transforms the carry-save form of the input number in to signed-digit form which is then recoded in the second stage so that it matches the form that the MB digits request. Recently, the technique of has been used for the design of high performance flexible coprocessor architectures targeting the computationally intensive DSP applications.
The conventional design of the AM operator requires that its inputs are first driven to an adder and then the input and the sum are driven to a multiplier in order to get output . The drawback of using an adder is that it inserts a significant delay in the critical path of the AM. As there are carry signals to be propagated inside the adder, the critical path depends on the bit-width of the inputs. In order to decrease this delay, a Carry-Look-Ahead (CLA) adder can be used which, however, increases the area occupation and power dissipation. 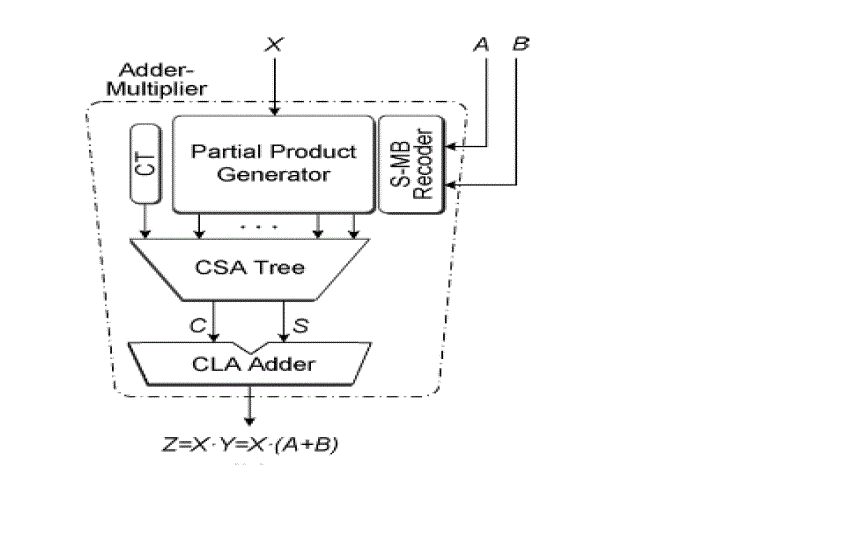An optimized design of the AM operator is based on the fusion of the adder and the MB encoding unit into a single data path block (Fig. 1) by direct recoding of the sum to its MB representation The fused Add-Multiply (FAM) component contains only one adder at the end (final adder of the parallel multiplier). As a result, significant area savings are observed and the critical path delay of the recoding process is reduced and decoupled from the bit-width of its inputs
The Partial Product Generator has hardware multipliers in that the generation of partial products is a necessary step in the process known to the art for efficient production of a final product. A way to increase the speed of hardware multipliers is through the use of the Booth algorithm. The alternate Booth partial product generation for hardware multipliers of the present invention is directed to a method and apparatus for eliminating the encoding of the bits of the multiplier prior to entering the partial product generating cell of the present invention which may result in less hardware and increased speed.In a Wallace tree multiplier the addition of bits with in one column is rearranged still further. Each column is characterized by the inputs to that column and the outputs from that column.
The inputs to a column are the bits of the partial product(Booth or non-Booth encoded) the carry bits from one column to the right . the sum bits that are generated within the column..The carry in comes CSA fashion from the previous column. The carry out goes CSA fashion to the next column.A carry-look ahead adder (CLA) is a type of adder used in digital logic. A carry-look ahead adder improves speed by reducing the amount of time required to determine carry bits. The carry-look ahead adder calculates one or more carry bits before the sum, which reduces the wait time to calculate the result of the larger value bitsThe generate function, Gi, indicates whether that stage causes a carry-out signal Ci to be generated if no carry-in signal exists. This occurs if both the addends contain a 1 in that bit. The propagate function, Pi, indicates whether a carry-in to the stage is passed to the carry-out for the stage. This occurs if either the addends have a 1 in that bit:Pi

A. S-Mb Recoder
A standard approach that might be taken by a novice to perform multiplication is to "shift and add", or normal "long multiplication". That is, for each column in the multiplier, shift the multiplicand the appropriate number of columns and multiply it by the value of the digit in that column of the multiplier, to obtain a partial product. The partial products are then added to obtain the final result:. It is possible to reduce the number of partial products by half, by using the technique of radix 4 Booth recoding.
The basic idea is that, instead of shifting and adding for every column of the multiplier term and multiplying by 1 or 0, we only take every second column, and multiply by ±1, ±2, or 0, to obtain the same results. So, to multiply by 7, we can multiply the partial product aligned against the least significant bit by -1, and multiply the partial product aligned with the third column by 2: The advantage of this method is the halving of the number of partial products. This is important in circuit design as it relates to the propagation delay in the running of the circuit, and the complexity and power consumption of its implementation.
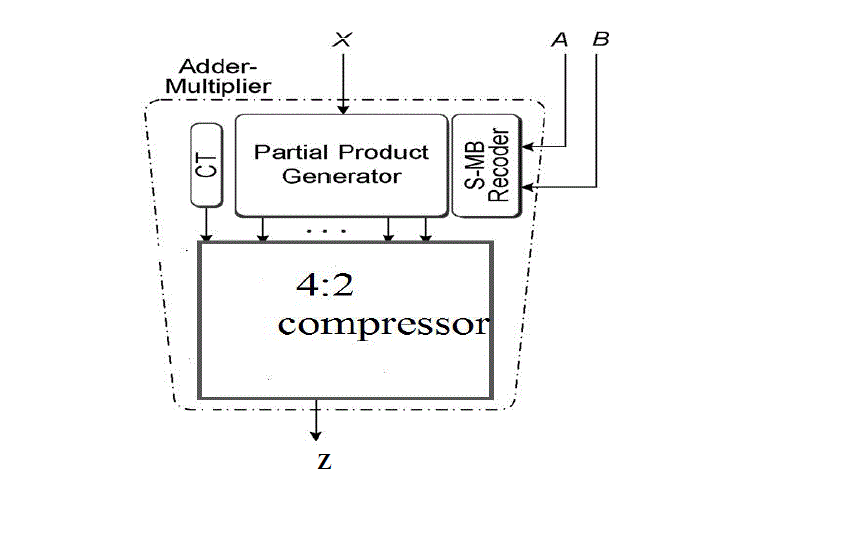
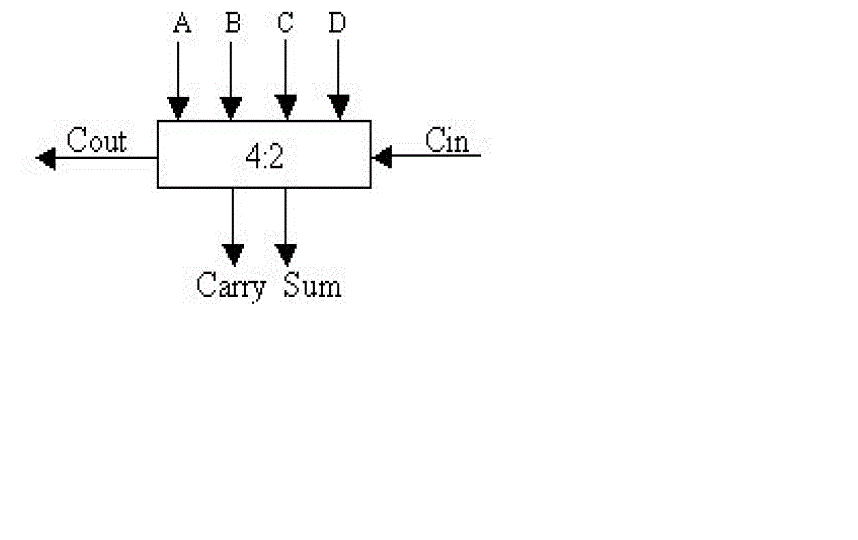
B. 4:2compressor
The characteristics of the 4:2 compressor are:
• The outputs represent the sum of the five inputs, so it is really a 5 bit adder
• Both carries are of equal weighting (i.e. add "1" to the next column)
• To avoid carry propagation, the value of Cout depends only on A, B, C and D. It is independent of Cin.
• The Cout signal forms the input to the Cin of a 4:2 of the next column.
4:2 compressors are all of their logical decompositions employ a series of XORs. In this way, the speed
comparison can be made independent of specific technologies though actual relative delays may be slightly different depending on specific circuit families and fabrication technologies employed. Many multiplier designs use specially designed counters and compressors depending on their processing technology.

V. SUM-PRODUCT IMPLEMENTATION
The direct recoding of the sum of two numbers in its MB form leads to a more efficient implementation of the fused Add-Multiply (FAM) unit compared to the existing. The efficient design of FAM operators are used to attain the optimization of the recoding for direct shaping of the MB form of the sum of two numbers (Sum to MB). The Sum- Modified Booth algorithm is structured, simple and can be easily modified in order to be applied in signed or unsigned numbers, which consist of odd or even number of bits. Sum-Modified Booth algorithm using unsigned and signed-bit Full Adders and Half Adders. The recoding technique reveals efficient solutions for the FAM design to obtain the targeted operator and timing functional for a larger range of frequencies. It obtains a significant improvement in both area and power consumption.
The fused Add-Multiply (FAM) contains only one adder at the end . As a result, significant area savings are observed and the critical path delay of the recoding process is reduced and decoupled from the bit-width of its inputs. We present a new technique for direct recoding of two numbers in the MB representation of their sum.compare to radix-2 representation radix-4 is more efficient . The area saving is the most significant, since in most signal processing applications, It can be employed to achieve high throughput . Each digit is represented by three bits named s, one and two. The sign bit shows if the digit is negative (s=1 ) or positive( s=0).

A. Radix4 Booth Recoding
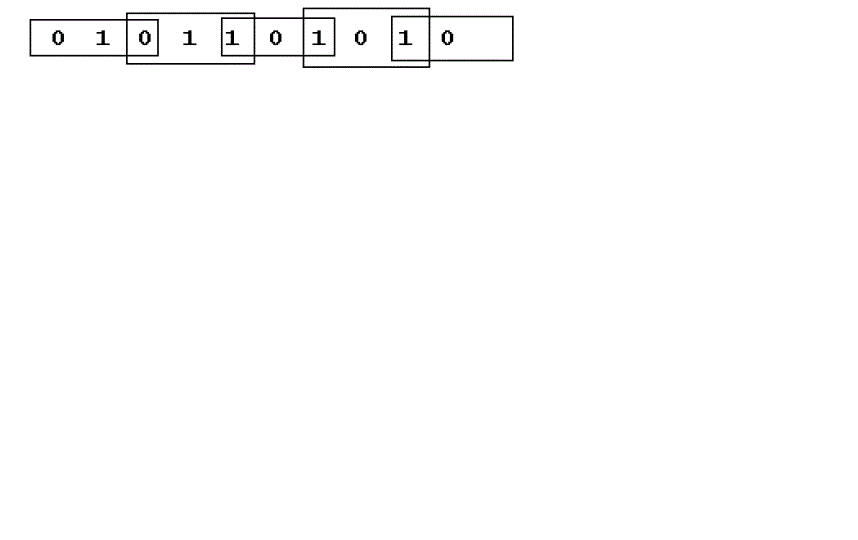
To Booth recode the multiplier term, we consider the bits in blocks of three, such that each block overlaps the previous block by one bit. Grouping starts from the LSB, and the first block only uses two bits of the multiplier since there is no previous block to overlap.
The overlap is necessary so that we know what happened in the last block, as the MSB of the block acts like a sign bit. Since we use the LSB of each block to know what the sign bit was in the previous block, and there are never any negative products before the least significant block, the LSB of the first block is always assumed to be 0. In the case where there are not enough bits to obtain a MSB of the last block, as below, we sign extend the multiplier by one bit. S-MB recoding technique is used to recode the sum of two consecutive bits of the input A(a2j,a2j+1 ) with two consecutive bits of the input B (b2j,b2j+1 ) into one MB digit so three bits are included in forming a MB digit. The most significant of them is negatively weighted while the two least significant of them have positive weight. in order to transform the two aforementioned pairs of bits in MB form we need to use signed-bit arithmetic. For this purpose we develop a set of bit-level signed Half Adders (HA) and Full Adders (FA) considering their inputs and outputs to be Signed. in this paper use two types of signed HAs referred as HA* and HA**.

B. S-MB1 RECODING
The recoding scheme is refered to as S-MB1 and it is obtained for both odd or even number of bit width of input numbers .The encoding of the modified booth digits yj mb,0<j<k-1 is based on both digits S2j+1 and S2j are extracted from the j recoding cell. A conventional full adder with inputs a2j,b2j,b2j-1 and produces the carry c2j+1.

C. S-MB2 RECODING
The recoding technique S-MB2 is described for even and odd bit-width of input numbers. consider the initial values c0,1=0 and c0,2=0. As in the S-MB1 recoding scheme, we use a conventional FA to produce the carry c2j+1 and the sum s2j .The inputs of the FA are a2j, b2j and c2j,1.The bit c2j,1 is the output carry of a conventional HA which is part of the (j-1)recoding cell and has the bits a2j-1,b2j-1 , as inputs. The HA* is used in order to produce the negatively signed sum and its outputs

D. S-MB3 RECODING
The third recoding technique is S-MB3 .we use a conventional FA to produce the carry c2j+1 and the sum s2j .The bit c2j,1 is now the output carry of a HA*which belongs to the (j-1) recoding cell and has the bits a2j-1,b2j-1 as inputs. The negatively signed bit s2j+1 is produced by a HA** in which we drive c2j+1 and the output sum (negatively signed) of the HA* of the recoding cell with the bits , as inputs a2j+1,b2j+1. The carry and sum outputs of the HA** are obtained

E. PERFORMANCE ANALYSIS
A theoretical analysis and comparative study in terms of area complexity and critical delay among three recoding schemes and the three existing recoding techniques. Our analysis is based on the unit gate model. More importantly for our quantitative comparisons and the 2-input primitive gates (NAND, AND, NOR, OR) count as one gate equivalent for both area and delay, whereas the 2-input XOR, XNOR gates count as two gate equivalent

VI. RESULTS AND DISCUSSION
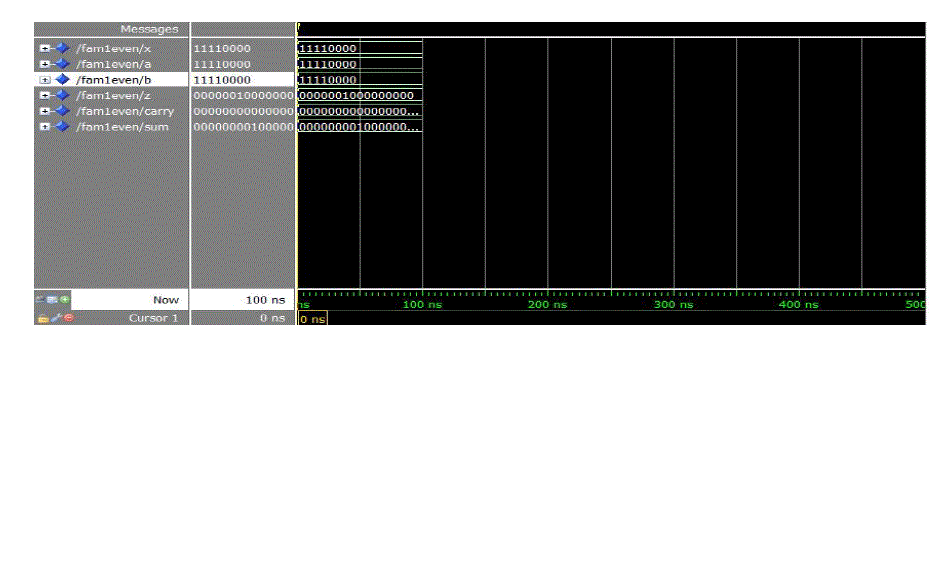
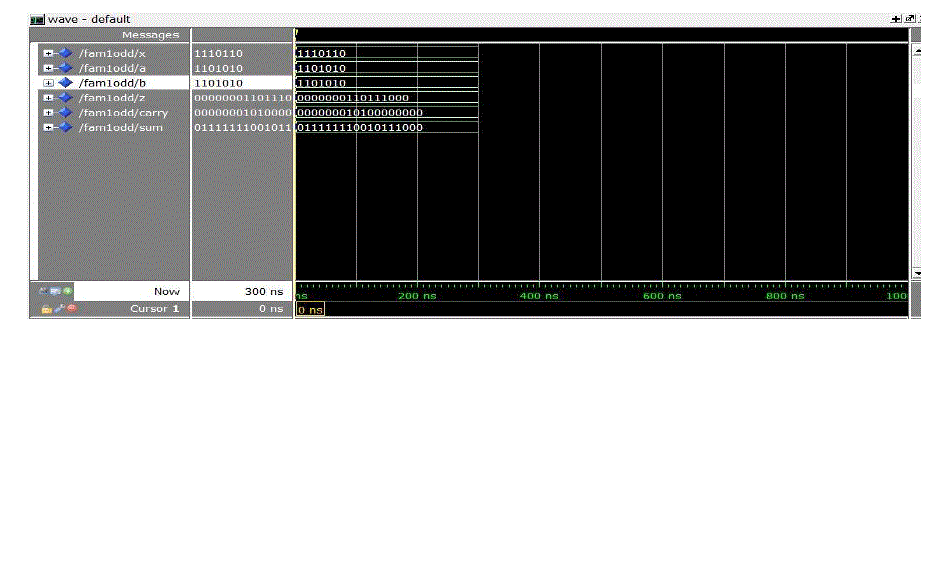
The performance of the three proposed recoding schemes in a fused sum-product operator and implemented them using structural Verilog HDL for both cases of even and odd bit-width of the recoder’s input numbers. We also synthesized all designs at lower frequencies in order to explore how they behave considering different timing is constraints in terms of area, timing and power consumption, we simulated the designs using Modelsim for the same set of pairs of input numbers in 2’s complement representation. The performance of the Fused sum- product designs include the proposed in recoding schemes with respect to the bit width of the input numbers. The lowest area and power values of each clock period are marked.

VII. CONCLUSION
The design of sum-product are used to implement the direct recoding of the sum of two numbers in its Modified Booth (MB) form to synthesize each Fused sum-product design at the highest achievable frequency. This paper also synthesized all designs at lower frequencies in order to explore how they behave different timing constraints in terms of area, timing and power consumption. The proposed recoding schemes (S-MB1, S-MB2 and SMB3) achieve area reduction . compare to existing recoders the power has been reduced. The performance of the Fused sum-product designs that include the proposed recoding schemes is considered with respect to the bit width of the input numbers. The area and power measurements of all Fused sum-product units for different clock periods for even (i.e., 8, 12, 16, 24 and 32 bits) and odd (i.e., 7,11, 15, 23 and 31 bits) bit-width of the recoder.

Tables at a glance
Table icon
Table 1
 

Figures at a glance
Figure 1 Figure 2 Figure 3
Figure 1 Figure 2 Figure 3
Figure 1 Figure 2 Figure 3
Figure 4 Figure 5 Figure 6
 

References