International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Implementation of Privacy Preservation of N-D Algorithms for Online Analytical Processing

Rohit Goel1, Mahesh Kumar2
  1. M.Tech Student, Dept. of CSE, Monad University, Hapur, India
  2. Assistant Professor, Dept. of CSE, Monad University, Hapur, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Online analytical processing (OLAP) is one of the most popular decision support and knowledge discovery techniques in business-intelligence systems.There are issues related to the protection of private information in Online Analytical Processing (OLAP) systems, where a major privacy concern is the adversarial inference of private information from OLAP query answers. This inference problem cannot be fully addressed by access control and data sanitization techniques.

Keywords
preservation, analytical, problem, privacy.

I. INTRODUCTION
In computing, online analytical processing, or OLAP is one of the most popular decision support and knowledge discovery techniques in business-intelligence systems. It is an approach to swiftly answer multi-dimensional analytical queries. OLAP is part of the broader category of business intelligence, which also encompasses relational reporting and data mining.
We address issues related to the protection of private information in Online Analytical Processing (OLAP) systems, where a major privacy concern is the adversarial inference of private information from OLAP query answers. Most previous work on privacy preserving OLAP focuses on a single aggregate function and/or addresses only exact disclosure, which eliminates from consideration an important class of privacy breaches where partial information, but not exact values, of private data is disclosed (i.e., partial disclosure). We address privacy protection against both exact and partial disclosure in OLAP systems with mixed aggregate functions.
Typical applications of OLAP include business reporting for sales, marketing, management reporting, business process management, budgeting and forecasting, financial reporting and similar areas, with new applications coming up, such as agriculture. The term OLAP was created as a slight modification of the traditional database term OLTP (Online Transaction Processing).
In particular, we propose an information-theoretic inference control approach that supports a combination of common according to its communication aggregate functions (e.g., COUNT, SUM, MIN, MAX, and MEDIAN) and guarantees the level of privacy disclosure not to exceed thresholds predetermined by the data owners. We demonstrate that our approach is efficient and can be implemented in existing OLAP systems with little modification. It also satisfies the simulate able auditing model and leaks no private information through query rejections.
Through performance analysis, we show that compared with previous approaches, our approach provides more effective privacy protection while maintaining a higher level of query-answer availability.

II. WHY PRIVACY PRESERVATION IS REQUIRED FOR OLAP?
The data warehouse server holds private data, and is supposed to answer OLAP queries issued by users on the multidimensional aggregates of private data. However, it is a challenge to enable OLAP on private data without violating the data owners’ privacy.
A user may not have the right to access all individual data points in the data warehouse, but might be allowed to issue OLAP queries on the aggregates of data for which it has no right to access.
In an OLAP system, a privacy breach occurs if a user can infer certain information about a private data point for which it has no right to access from the query answers it receives as well as the data that it has the right to access. Such privacy breach is referred to as the inference problem.
Example:
In a hospital system, the accounting department (as a user) can access each patient’s financial data, but not the patients’ medical records.
Nonetheless, the accounting department may query aggregate information related to the medical records, such as the total expense for patients with Alzheimer’s disease.

III. INFERENCE PROBLEM
In an OLAP system, a privacy breach occurs if a user can infer certain information about a private data point for which it has no right to access from the query answers it receives as well as the data that it has the right to access.
Such privacy breach is referred to as the inference problem. If owner of the cube makes Attribute Y of collection 1 as sensitive cell, then users do not have access to that sensitive cell, but they can request aggregate queries.
Suppose a user asks 2 queries:
1. What is the total no. of items in collection1?
2. What is the value of attribute X in collection 1?
Answer 1. 47
Answer 2. 7
Inference: The no. of items of Y in collection1 is 47-7=40.
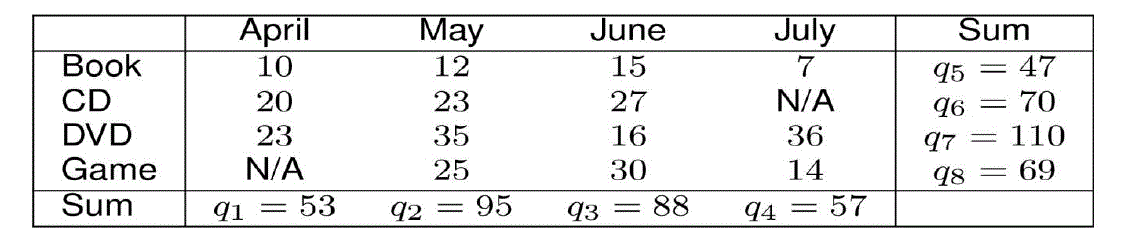Example of Inference Problem
So the user is able to get the value of sensitive cell for which it has no access by requesting aggregate queries on the data.
So “Privacy Breaching” as user should not get value of sensitive cell but here it can be inferred.

IV. OLAP SYSTEM MODEL
Consider OLAP as a system where the data warehouse server stores data in an n-dimensional data cube, in order to support aggregate queries on an attribute-of-interest over selected data.
We refer to such attribute-of-interest as the measure attribute. Besides the measure attribute, there are n dimension attributes, each of which is represented by a dimension of the data cube.
Each (base) cell of the data cube is the value of the measure attribute for the corresponding value combination of dimension attributes.
For example
Table shows a two-dimensional data cube with a measure attribute of sales and two dimension attributes of product and time.
Each cell of the data cube in Table is the sales amount (i.e., measure attribute) of a product (e.g., Book) in a month (e.g., April). As in real cases, some cells in the data cube can be missing or not applicable.

V. INFERENCE CONTROL
There are two types of methods that have been proposed to prevent inference problems from happening in OLAP systems:
1. Inference Control
2. Input/output perturbation.
1. Inference control:
In the inference control approach, after receiving a query from a user, the data warehouse server determines whether answering the query may lead to an inference problem, and then either rejects the query or answers it precisely.
2. Input/output Perturbation:
The input/output perturbation approach either perturbs (input) data stored in the data warehouse server with random noise and answers every query with estimation, or adds random noise to the (output) query answers in order to preserve privacy
But for decision making precise or exact answer is required, therefore inference control is better way for privacy information.

VI. IMPLEMENTATION AND RESULTS
1. INFERENCE CONTROL ALGORITHM (for n-d Arbitrary Distribution
Require: h-dimensional query q on sub-cube (a1… an-h, ALL… ALL), lo =0.
1: {When a query q is received.}
2: if function of q is MIN-like then
As we can see, only lp needs to be updated for MIN-like queries while all four parameters are updated for SUM-like ones.
In the starting we are using “Analytical Workspace Manager” to analyze the data cube and to map the dimensions of data cube on corresponding tables of database. Then, these tables are used in program for query evaluation and query answering.
Here, instead of maintaining μk and σk values for each user, we are maintaining μk and σk values for each sub cube of query history.
3. ASSUMPTIONS
1) The algorithm is for n-dimensions.
2) The query must be entered in a special manner
a) After every word space has to be given.
b) First word of the query belongs to the aggregate function
c) All the words except the first one are names of dimensions.
d) Each query gives the value of measure attribute. e.g.- sum april
3) Our implementation gives whether the query must be answered or not.

Modification made in the algorithm
2.It is maintaining 3 text files
a) “dimensions.txt”- It is a text file containing the names of tables (dimensions) to be accessed by our program.
b) “queryhistory.txt”- It is a text file containing the sub cubes of answered queries
c) “uk_sk.txt”- It is a text file containing corresponding μk,σk and lp values.
3. Program Details:
a) As soon as the program starts, db_data_retrival() establishes connection with database and get_queryinfo() takes query from the user and classifies it into “MIN like” or “SUM like” query.
b) transfer2() and transfer() functions transfer corresponding μ k,σk and lp values of each subcube and subcube history into related data structures.
c) Depending on type of query, query_evaluate() evaluates the query and answers it if lo+pp< l where lo = information accessed by the query, lp=information accessed earlier l=level at which privacy breach takes place.
4.
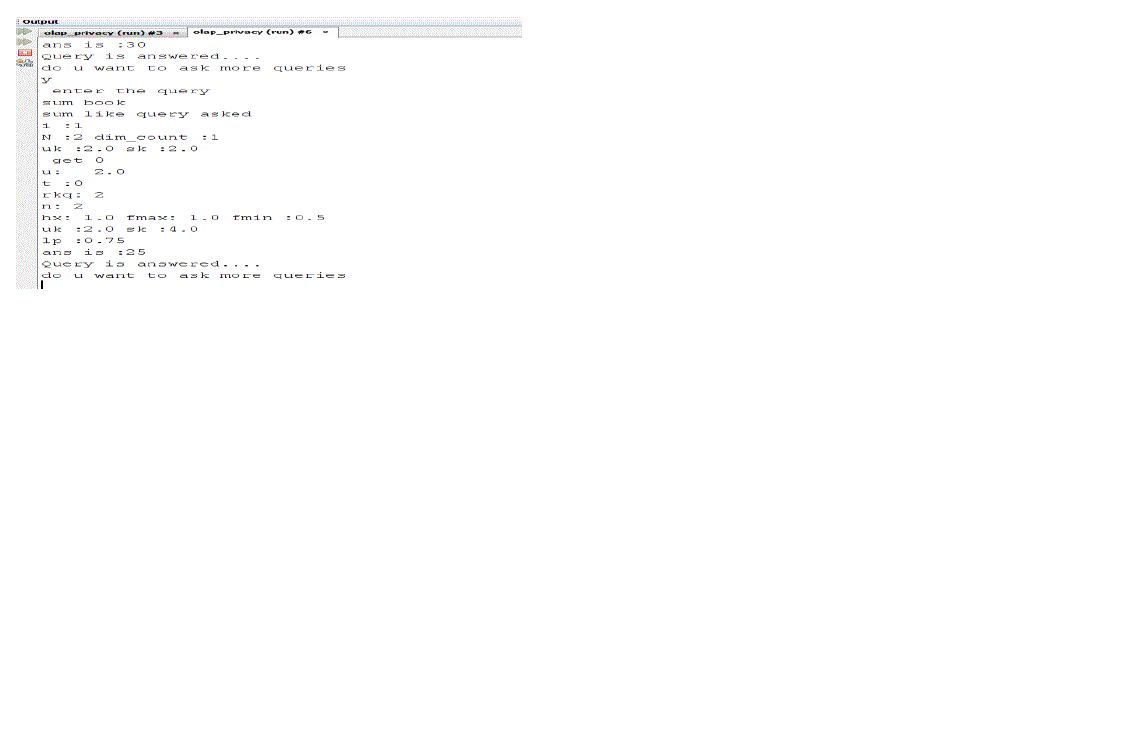
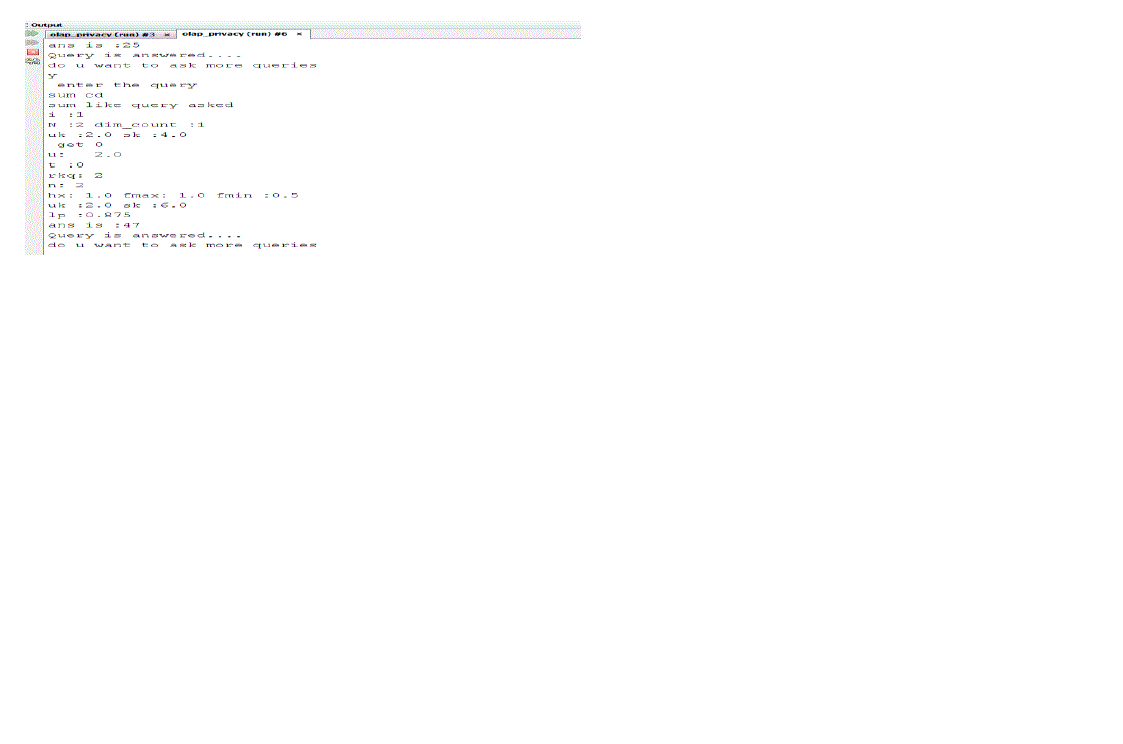
a) Query asked: sum april
Output: Query is answered
b) Query asked: sum book
Output: Query is answered
c) Query asked: sum cd
Output: Query is answered.
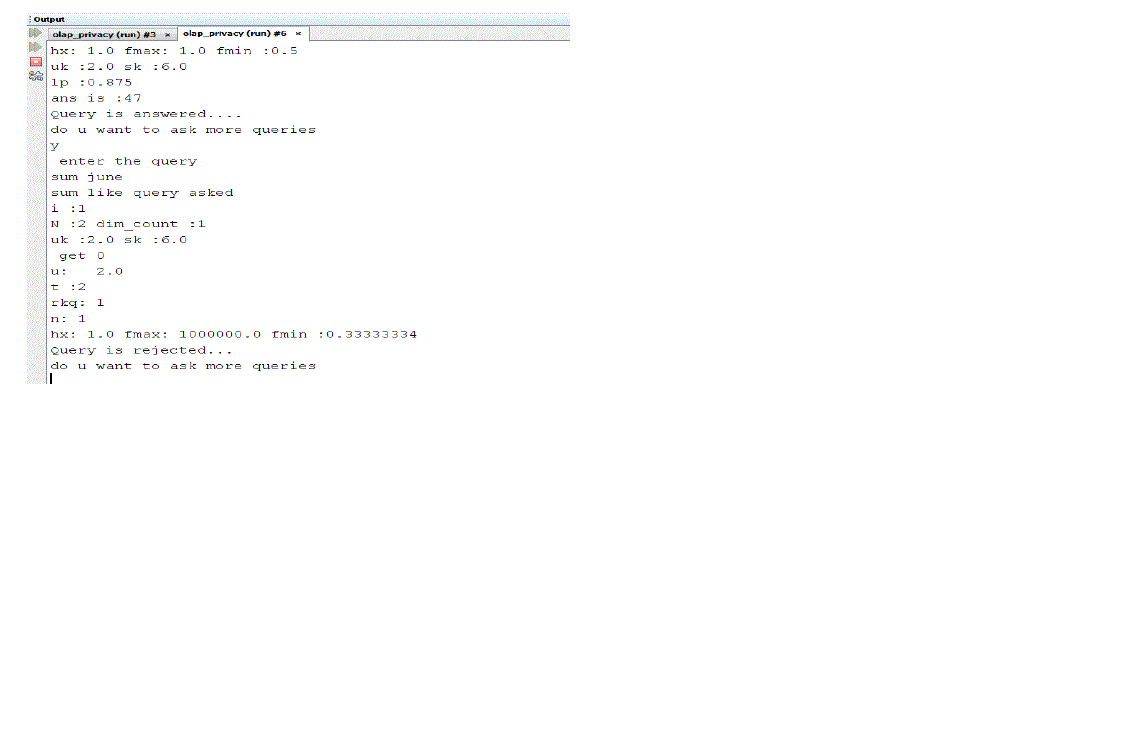
d) Query asked: sum june
Output: Query is rejected
5. Updated text files are
a) “Queryhistory.txt”- containing the subcube of answered queries.
b) “uk_sk.txt” –containing the corresponding μk,σk and lp values of answered query’s subcube

V. CONCLUSION
For implementing Inference Control Algorithm (A Generic n-d Algorithm), we have used “Analytical Workspace Manager” for building, analysing and mapping values. We have used Oracle 11g for database and mapped values on database tables with the help of “Analytical Workspace Manager”.
 
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 4.2 Figure 4.3 Figure 4.4 Figure 4.5 Figure 4.6
Figure 1 Figure 2 Figure 3 Figure 4
Figure 4.7 Figure 4.8 Figure 4.9 Figure 4.10
 

References