Keywords
|
| Discrete Fourier transform (DFT), Fast Fourier transform (FFT), Inverse Fast Fourier transform (IFFT), general split radix, radix 3/6, System Verilog language. |
INTRODUCTION
|
| Discrete Fourier Transform (DFT) is one of the most important tools used in almost all fields of science and engineering. DFT can be implemented with efficient algorithms generally classified as Fast Fourier transforms (FFT). The most widely used approaches are so-called the algorithms for 2m, such as radix-2, radix 4 and split radix FFT (SRFFT). Considerable researches have carried out and resulted in the rapid development on this class of algorithms. Simultaneously, the researches on the algorithms for computing length-N=km DFT have resulted in the presentation of the methods for and k=3 and k=6. |
| Due to the poor efficiency, the algorithms for km are of trivial practical meanings when k ≠ 2. However, there exist many applications in which the sequence lengths are 3m or 6m. The idea of this letter is to develop a useful algorithm for length N=6m DFT. The available published algorithms are reported in; it seems that the general split radix algorithm is more adequate for the length- DFT. In this letter, we propose an algorithm based radix-6 approach. The algorithm is implemented with more efficient than the reported ones. Its computational Complexity is approximately equal to the equation given as 4.071Nlogïÿýïÿý N-5.61N+33.555logïÿýïÿý N-130.992 which is close to that of standard SRFFT (The complexity of SRFFT is 4Nlogïÿýïÿý N-6N+8). The proposed algorithm is a radix 3/6 algorithm and uses base (1, j). The algorithm decomposes a DFT of size N=6m into one length- N/3 and four length-N/6 sub DFTs. The flexibility of the decomposition enables the algorithm is competent at the implementation of a non-power-of-six DFT, while its length can exactly divided by 6. Appropriate permutations are used for sub DFTs input sequences to reduce the computational intension. |
LITERATURE SURVEY
|
a. Radix 2/8 FFT algorithm for length qx2m
|
| A new radix-2/8 Fast Fourier Transform (FFT) algorithm have been proposed for computing the Discrete Fourier transform of an arbitrary length N= qx2^m,where m is an odd integer. It reduces substantially the operations such as data transfer, address generation, and twiddle factor evaluation or access to the lookup table, which contribute significantly to the execution time of FFT algorithms. It is shown that the arithmetic complexity (multiplications, additions) of the proposed algorithm is, in most cases, the same as that of the existing split-radix FFT algorithm. The basic idea behind the proposed algorithm is the use of a mixture of radix-2 and radix-8 index maps. The algorithm is expressed in a simple matrix form, thereby facilitating an easy implementation of the algorithm, and allowing for an extension to the multidimensional case. For structural complexity, the important properties of the Cooley–Tukey approach such as the use of the butterfly scheme and in-place computation are preserved by the proposed algorithm. It is suitable only for DFT of sequence length N=qx2m |
b. Radix 2/16 FFT algorithm for length qx2m
|
| A radix-2/16 decimation-in-frequency (DIF) fast Fourier transforms (FFT) algorithm and its higher radix version, namely radix-4/16 DIF FFT algorithm, have been proposed by suitably mixing the radix-2, radix-4 and radix-16 index maps, and combing some of the twiddle factors [3]. It is shown that the proposed algorithms and the existing radix-2/4 and radix-2/8 FFT algorithms require exactly the same number of arithmetic operations (multiplications and additions). By using this technique, it can be shown that all the possible split-radix FFT algorithms of the type radix- 2r/2rs for computing a 2m DFT require exactly the same number of arithmetic operations. This algorithm is suitable only for sequence of length N=2m, m is integer. |
IMPLEMENTATION OF PROPOSED RADIX 3/6 ALGORITHM
|
| A new radix-6 FFT algorithm suitable for multiply-add instruction have been proposed. The new radix-6 FFT algorithm requires fewer floating-point instructions than the conventional radix-6 FFT algorithms on processors that have a multiply-add instruction. Techniques to obtain an algorithm for computing radix-6 FFT with fewer floatingpoint instructions than conventional radix-6 FFT algorithms have been proposed. The number of floating-point instructions for the new radix-6 FFT algorithm is compared with those of conventional radix-6 FFT algorithms on processors with multiply-add instruction. |
| The definition of the Discrete Fourier Transform is given by |
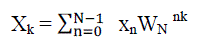 |
| Where |
| WN =e π , j=√−1, the length of sequence |
| {xn} is assumed as an integer which is divisibly by six. For lengths N of DFT, powers-of-six would be best for the proposed algorithm. Obviously, the DFT can be divided into three length-N/3 sub-DFTs. In order to derive a best possible algorithm, we continue to decompose the three sub-DFTs. Due to no scaling factor in front of it; the first sub- DFT should be let as-is and directly go into the recursive decomposition of the next stage. The other two sub-DFTs are divided into four sub-DFTs of length-N/6.Actually, if the length of a DFT can be divided by 6, the DFT can be definitely decomposed by the algorithm. The generalized length-N can be assumed as the N= 2rx3m, where as r ≥ m-1. The decomposition of a DFT of size N= 2rx3m denoted by |
 |
| Where the four length-N/6 sub DFTs are reordered. To simplify the description, (2) can be expressed |
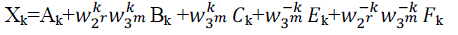 |
| Where |
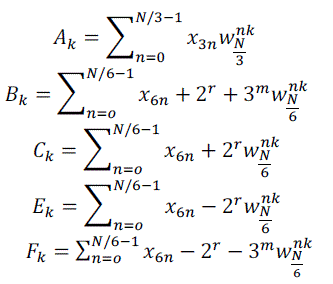 (4) (4) |
| In (3), Bk and Fk can be treated in pairs, since and is a conjugate-pair. In the similar way, Ck and Ek can be handled with in pairs. The direct implementation of (3) performs many unnecessary operations, since the computations of Xk, X2N/6+k, X4N/6+k,XN/6+k, X3N/6+k and XNN/6+k turn out to share many calculations each other. In particular, if we add N/6 to K, the size- DFT are not changed (because they are periodic in), while the size-N/3 DFT is unchanged if we add 2N/6 to K. So, the only things that changes are , , and terms. In order to reduce the number of the operations, the following six identities are necessary, |
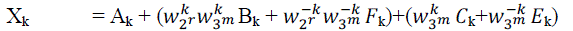 (5) (5) |
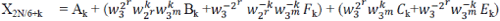 (6) (6) |
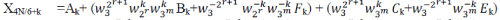 (7) (7) |
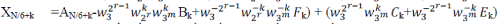 (8) (8) |
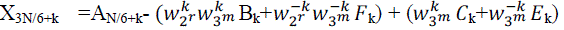 (9) (9) |
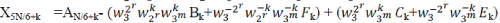 (10) (10) |
| A complete output X {k} set can be obtained if we let range from 0 to N/6 -1 in the above six equations. |
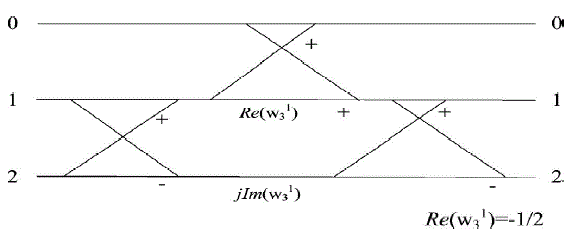
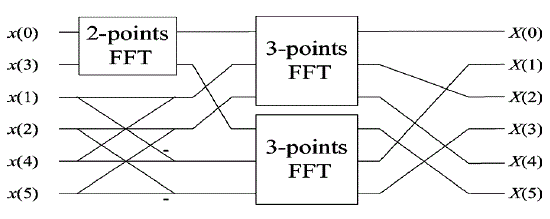
| We now summarize the scheme of the proposed radix-3/6 FFT algorithm. The initial input sequence {xn} of length-N is decomposed into five sub-sequences. This process is repeated successively for each of new sub-sequences, until the sizes of all sub DFTs are indivisible by 6. Figs. 1–3 illustrate the flow graph of 3, 6 and 12-point radix 3/6 algorithm (2-points and 4-points FFT can be performed with SRFFT). |
| The 3-points DFT requires 4 real multiplications and 12 real additions (some algorithms assume that a 3- points DFT is calculated with 2 real multiplications and 12 real additions since one need not multiply ½ and the multiplication by 1/2 can be evaluated with bit shift). |
| The initial input sequence {ïÿýïÿýïÿýïÿý} of length- N is decomposed into five sub-sequences. This process is repeated successively for each of new sub-sequences, until the sizes of all sub DFTs are indivisible by 6. |
| The Radix-3/6 DIF FFT can be derived as follows |
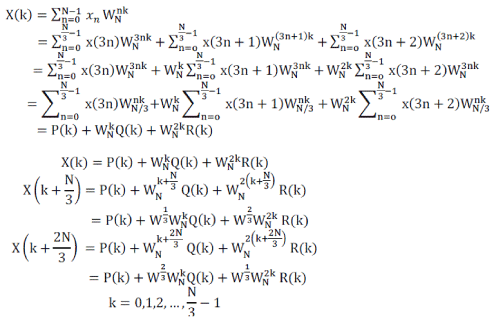 |
| Each of the sums, P (k), Q (k), and R (k), in is recognized as an N/3-point DFT. The transform X (k) can be broken into three parts as shown in equation (11). |
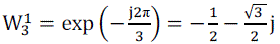 |
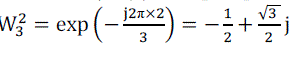 |
| The decomposition in the proposed algorithm is conducted recursively until the lengths of all sub DFTs cannot be exactly divided by 6. In general, there are only 1 the first special butterfly (if r≥1and m≥1), 1 the second special case butterfly (if r≥2and m≥1), 1 the third special case butterfly and 1 the fourth special case butterfly (if r≥3and m≥1). The total number of the fifth and sixth type of butterflies is 2ïÿýïÿýïÿýïÿýïÿýïÿý-4.Thus, the arithmetic complexity of the proposed algorithm can be given in below equation (14). |
 |
RESULTS AND DISCUSSION
|
| The 12 point DFT sequence has been implemented in System Verilog and simulated using Modelsim Version 6.4. |
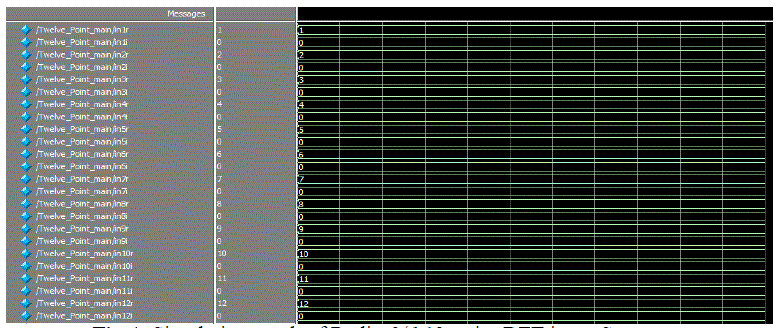
| The, Fig.4 shows the input sequence of radix-3/6 algorithm for 12-point FFT i.e.,{ïÿýïÿýïÿýïÿý}={1,2,3,4,5,6,7,8,9,10,11} applied to the Modelsim for simulation. |
| The, Fig.5 shows the output sequence Xk={78,-6+22.3923i,-6+10.39i,-6+6i,-6+3.464i,-6+1.6i,-6,-6-1.6i,-6-3.4i, -6-6i,- 6-10.39i,-6-22.3923i} for the given input sequence. |
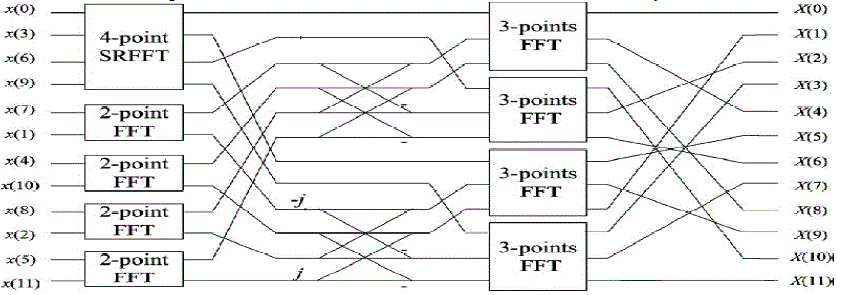
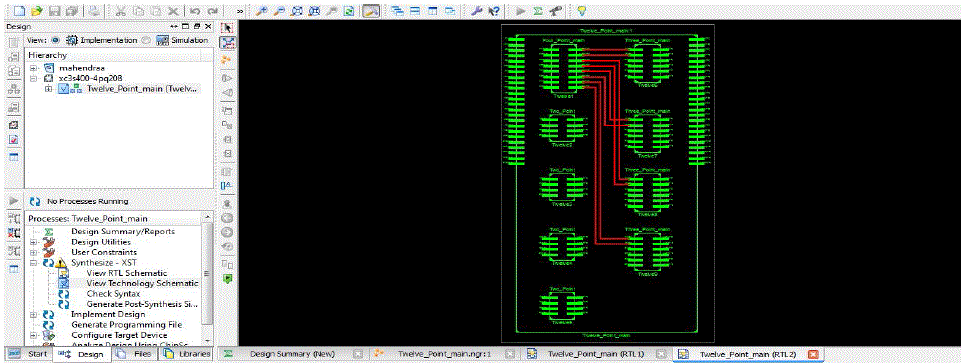
| The above figure.6 is the RTL (Register Transfer Level) Schematic for 12 point input sequence using radix 3/6 algorithm generated in Xilinx 9.1i. The schematic contains one 4-point SRFFT, four 2-point FFT and three 3-point FFTs butterfly blocks. |
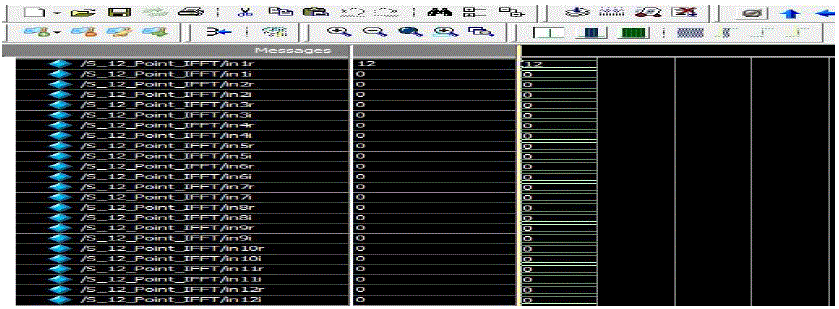
| The Fig.7 Shows the simulation results of 12-Point Split Radix 3/6 IFFT input sequence {Xk}={12,0,0,0, 0,0,0, 0,0,0, 0,0} applied to the Modelsim for simulation. |
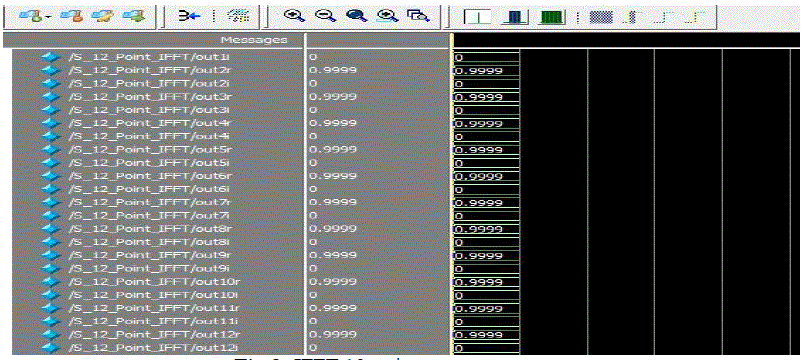
| The Fig.8 Shows the simulation results of 12-Point Split Radix 3/6 IFFT output sequence {ïÿýïÿýïÿýïÿý} = {0.999, 0.999, 0.999, 0.999, 0.999, 0.999, 0.999, 0.999, 0.999, 0.999, 0.999, 0.999}. |
FUTURE SCOPE
|
| Implementation of 16 Point RADIX 3/6 FFT Design using Verilog and verification using system Verilog will be done. These implementations usually employ efficient fast Fourier transform (FFT) algorithms so much so that the terms "FFT" and "DFT" are often used interchangeably. The terminology is further blurred by the (now rare) synonym finite Fourier transform for the DFT, which apparently predates the term "fast Fourier transform" but has the same initialize. |
CONCLUSION
|
| A radix 3/6 FFT algorithm is presented for length-6m DFT. The proposed algorithm is a mixture of radix-3 and radix-6 algorithm. It can evaluate a non-power-of-six DFT, as long as its length-6m can be divided by 6. In order to reduce the number of operations, all sub DFTs are reordered favourably. The proposed algorithm shows that its implementation requires less real operations as compared with the published algorithms. Its arithmetic complexity is about, which is close to that of standard SRFFT. Due to being an irregular integer for the sequence lengths, it is difficult to gain a completely accurate formula of computational complexity. |
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
 |
 |
 |
 |
| Figure 5 |
Figure 6 |
Figure 7 |
Figure 8 |
|
References
|
- M. Frigo and S. Johnson, “The design and implementation of fftw3,” Proc. IEEE, vol. 93, no.2, pp. 216–231, 2005.
- J. Keiner, S. Kunis, and D. Potts, “Using nfft 3—A software library for various nonequispaced fast Fourier transforms,” ACM Trans. Math. Softw.(TOMS), vol. 36, no. 4, pp.19–19, 2005.
- D. Sepiashvili, “Performance Models and Search Methods for Optimal FFT Implementations,” M.Sc. thesis, Carnegie Mellon Univ., Pittsburgh, PA, 2000.
- J. Cooley and J. Tukey, “An algorithm for the machine calculation of complex Fourier series,” Math.Comput, vol. 19, no. 90, pp. 297–301, 1965.
- P. Duhamel and H. Hollmann, “Split-radix FFT algorithm,” Electron.Lett., vol. 20, pp. 14–6, Jan. 1984.
- Kamar and Y. Elcherif, “Conjugate pair fast Fourier transform,” Electron. Lett., vol. 25, no.5, pp. 324–325, Apr. 1989.
- S. Bouguezel, M. Ahmad, and M. Swamy, “A new radix-2/8 FFT algorithm for length-DFTs,” IEEE Trans. Circuits Syst.I, vol.51, no. 9, pp. 1723–1732, Sep. 2004.
- E. Dubois and A. Venetsanopoulos, “A new algorithm for the radix-3 FFT,” IEEE Trans. Acoust., Speech, Signal Process,, vol. ASSP-26, pp.222–225, Jun. 1978.
- S. Prakash and V. Rao, “A new radix-6 FFT algorithm,” IEEE Trans. Acoust., Speech, Signal Process., vol. ASSP-29, no. 4, pp. 939–941,Aug. 1981.
- Y. Suzuki, T. Sone, and K. Kido, “A new FFT algorithm of radix 3, 6, and 12,” IEEE Trans. Acoust., Speech, Signal Process., vol. ASSP- 34,no. 2, pp. 380–383, Apr. 1986.
|