I. INTRODUCTION
|
| Cryptography is the art and science of transforming information in order to make it secure from unintended recipients or use. The two basic building blocks of encryption techniques used in block ciphers are substitution and transposition. In substitution technique the plaintext letters are replaced by some other letter but in transposition technique, shuffling of bits is performed, by applying some permutation on them. Worldwide encryption standards such as DES (Data Encryption Standard), AES (Advanced Encryption Standard) and EES (Escrowed Encryption Standard) have been - and some of them still are — extensively used to solve the problem of communication over an insecure channel. But, with today‘s advanced technologies they seem not to be as secure and fast as one would like. In this paper, we have proposed symmetric encryption technique which has two advantages over traditional schemes based on Feistel ciphers. First, the Encryption and decryption procedures are much simpler, and consequently much faster. Second, the security level is higher due to the inherent poly-alphabetic nature of the substitution mapping method used in the encryption process and the transpose operations performed after a level one cipher text generation. |
II. LITERATURE REVIEW
|
| In 1997 the National Institute of Standards and Technology announced a competition for the algorithm‘s(DES)[1] replacement and held public meetings to discuss the criteria for a proposed Advanced Encryption Standard (AES)[6]. In 1999 NIST announced the five finalists: MARS[12], RC6[13], Rijndael[14], Serpent[15], and Twofish[16]. MARS breaks the 128-bit input block into four 32-bit words. MARS uses a 32-round unbalanced Feistel network: in each round one data word and some key words modify the remaining data words. RC6, a 20-round Feistel cipher out of RSA Security Inc., is much simpler. ?Pre-whitening? and ?Post whitening? steps have been used to increase the strength of algorithm, whitening is a simple idea to Xor the key material with the input or output material. Twofish, is a 16- round Feistel network with two modifications. One is a one-bit rotation before and after the data enters the round function. The other alteration is dynamic S-boxes. In serpent ,there are 32 rounds—a high number—each of which consists of XORing the key and the intermediate data, a pass through Sboxes, and a linear function that combines fixed rotations and XOR. Bruce Scheneir[17] proposed a fast and unpatented block cipher available freely to people for public use. Blowfish[18] is a secret-key block cipher, is a Feistel network, iterating a simple encryption function 16 times. The block size is 64 bits, and the key can be any length up to 448 bits. Although there is a complex initialization phase required before any encryption can take place, the actual encryption of data is very efficient on large microprocessors. |
III. PROPOSED ALGORITHM
|
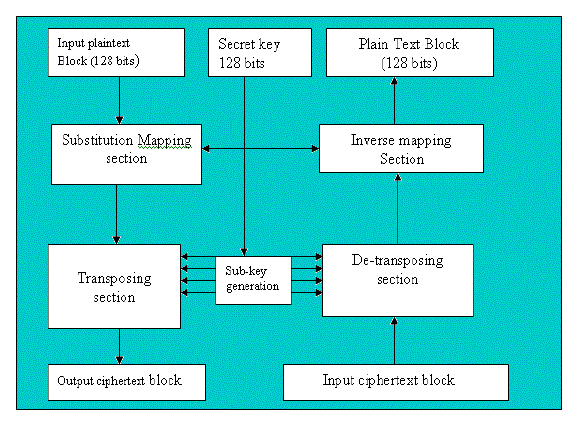
| FPSKEA is a block cipher, which takes input of 128 bits of plaintext block and 128 bits of key to produce 128 bits of ciphertext block. It is a product cipher based on multiple applications of substitution-permutation combinations hence is a SP-network based cipher. It‘s basic architecture is explained in the following figure. |
| Above architecture clearly shows the encryption and decryption process used for converting plaintext into ciphertext and from ciphertext back to plaintext respectively. During encryption, the given plaintext message is divided into blocks of 16 characters each (equivalent to 128 bits) then each block of 128 bits is passed through substitution mapping section, which transforms the given plaintext block (128 bits ) into level one cipher text block(128bits), using key of 128 bits. This level one cipher text block is now fed into the transposition section, which transforms the level one cipher text block into final ciphertext block using four sub keys derived from original key to be used in this transposition section combined with permutation operations. If ?n‘ are the number of blocks in a given message, above written procedure is repeated ?n‘ number of times to transform complete plaintext message into ciphertext message. |
| The reverse process that is decryption which transforms the ciphertext block into plaintext blocks is also shown in the figure 5.1. In the decryption process, ciphertext block(128 bits) is passed through Detransposition section first, which converts it into level one ciphertext block by using four sub keys derived from original key(128 bits) and by applying reverse permutation operations. This level one cipher text block is then passed through inverse mapping section, which produces the original plaintext block, by using the key and reverse substitution operations. |
The Encryption Process
|
| The encryption method consist of three simple steps |
| 1) Matrix initialization using characters of secret key and |
| 2) Substitution mapping using the S-BOX (matrix) and |
| 3) Transposition operation using arrays and sub-keys. |
IMPLEMENTAION OF THE PROPOSED ALGORITHM
|
| STEP.1 Initial Matrix Structure |
| A matrix with sixteen rows and ninety five columns is defined. Columns in every row of the matrix is filled with ASCII codes of characters starting from BLANK (ASCII = 32) in column zero to (ASCII = 126) in column ninety four representing elements of the matrix. |
| Code 1 Initialization Process. |
| For i =0 to15 |
| For j =0 to 94 |
| M[i][j]=j+32 |
| EndFor |
| Code.1: Initialization of Matrix M with ASCII code of plaintext characters |
| A 16 character (128 bits) secret key K with key characters k[0] through k[15] is used for encryption and decryption. The ith row of the matrix is given an initial right circular shift, as many numbers of times as equal to the ASCII code of (i+1)th key character to shuffle the contents of the matrix m, for i=0 to 14. for example if k[1] is ?a‘ whose ASII value is 97, row 0 of the matrix M should be right circular shifted 97 times. |
| Code2. Circular Shift Operation Applied To The Rows Of The Matrix M. |
| For i=0 to 14 |
| n=ASCII(k(i+1)) |
| For m=0 to n |
| For j=94 to 0 |
| M[i][j+1]=M[i][j] |
| EndFor |
| EndFor |
| n=ASCII(k[0]) |
| Form=0 to n |
| For j=94 to 0 |
| M[15][j+1]=M[15][j] |
| EndFor |
| M[15][0]=M[15][95] |
| EndFor |
| These right circular operations make the arrangements of the contents of the matrix known only to the sender and receiver of the message but not to an adversary as the key is unknown to him. |
| Further the ith row of the matrix is given a second right circular shift as many number of times as equal to ASCII (K(i)) to shuffle the contents of the matrix M, for i=0 to 15. For example, the row 0 of M is right circular shifted as many number of times as equal to the ASCII value of K[0] . The row 1 of the matrix M is give a right circular shift as many number of times as equal to the ASCII value of the key character K[1] and so on. |
| Code 3 Second Circular Shift Operation Applied To The Rows Of Matrix M. |
| For i = 0 to 15 |
| n = ASCII (K[i]) |
| For m = 0 to n |
| For j = 94 to 0 |
| M [i][j+1] = M[i][j] |
| EndFor |
| M[i][0] = M[i][95] |
| EndFor |
| EndFor |
| These shifting operations ensure that no adversary will not be able to find a reference from which he/she can start working out to extract the secret key even if he/she is able to obtain a plain text message and the corresponding cipher text message. These circular right shift operations on the rows of the matrix M are done only once, before the beginning of an encryption section. |
| Substitution Mapping Procedure |
| Code 4 shows the mapping process used in converting plain text character blocks into level 1 cipher text character blocks. A given message if broken into blocks of 16 plain text characters. The character p[i] is taken and the number if calculated such that j = ASCII code of plain text character p[i] – 32. This number j, is used as column number of the matrix M. Using j as column number we proceed to find the element in the ith row of the matrix. This element is used as level 1 cipher text character cL1[i] for a given plain text character p[i]. For example, for the plain text character P[0] in a block i =0, j=ASCII code of plain text character p[0]- 32 is used as column number of row 0 of the matrix M to obtain level one cipher text character corresponding to P[0]. In this way, all the 16 plain text characters in a block are mapped into 16 level1 cipher text characters denoted by cL[i], i = 0 to 15. |
| Code 4 Mapping of plain text characters in a block to level1 cipher text characters. |
| For i = 0 to 15 |
| J = ASCII (p[i] – 32) |
| cL1[i] = M[i][j] |
| EndFor |
| Step 2. Transposition |
| The level1 cipher text character cL1[i] in a block of 16 produced using the matrix M are further transposed using arrays whose elements are circular shifted left and right using sub-keys derived from the secret key. This operation makes the resulting output cipher text characters extremely difficult to decrypt by any adversary without having the secret key. |
| Sub-Key Generation |
| Four sub-keys ks1, ks2, ks3 and ks4 are generated using the characters of the secret key K such that: |
| Ks1 = (sum of ASCII codes of characters of k MOD 13) +1 |
| 1<=ks1<=13 |
| Ks2 = (sum of ASCII codes of characters of k MOD 5) +1 |
| 1<=ks2<=5 |
| Ks3 = (sum of ASCII codes of characters of k MOD 6) +1 |
| 1<=ks3<=6 |
| Ks4 = (sum of ASCII codes of characters of k MOD 14) +1 |
| 1<=ks4<=14 |
| Code 5 The Sub-Key Generation Procedure |
| n=o |
| For i = 0 to 15 |
| n = n+ ASCII (K[i]) |
| EndFor |
| ks1 = (n % 13) +1 |
| ks2 = (n % 5) +1 |
| ks3 = (n % 6) +1 |
| ks4 = (n % 14) +1 |
| Step 3.Transposition of Level-One Cipher Text Characters by Arrays. |
| The characters in the level-one cipher text character block (CL1(0) through CL1(15)) are transferred to a 16 element array A1. The array A1 is right circular shifted as many number of times as equal to the integer value of Ks1. After this operation, the first eight elements of A1(left most elements) are transferred to another array A2 having 8 element positions. Then, A2 is right circular shifted as many number of times as equal to the integer value of Ks2. The other eight elements of the array A1(rightmost elements) are transferred to another 8 element array A3 which is left circular shifted as many number of times as equal to integer value of Ks3. Then A2 and A3 are concatenated and transferred to a 16 element array A4. This 16 element array, A4.is right circular shifted as many number of times as equal to the integer value of Ks4. |
| The Transposition Operation Performed on Level-One Cipher Text Characters |
| Transfer level-one cipher text block to Array A, |
| For i = 0 to 15 |
| A1[i]=CL1[i] |
| EndFor |
| Right circular shift level-one cipher textblock in Array A1 using sub-key ks1 |
| For n = 0 to ks1 |
| For i = 15 to 0 |
| A1[i+1]=A1[i] |
| EndFor |
| A1[0]=A1[16] |
| EndFor |
| Transfer half of Array A1 to Array A2 and right circular shift using sub-key ks2 |
| For i = 0 to 7 |
| A2[i]=A1[i] |
| EndFor |
| For n = 0 to Ks2 |
| For i = 7 to 0 |
| A2[ i+ 1] = A2[ i ] |
| EndFor |
| A2[0]=A2[8] |
| EndFor |
| Transfer other half of Array A1 to Array A3 and left circular shift using sub-key ks3. |
| For i = 0 to 7 |
| A3 [i] = A1[i + 8] |
| EndFor |
| For n = 0 to Ks3 |
| A3[8] = A3[0] |
| For i =0 to 7 |
| A3[i]=A3[i+1] |
| EndFor |
| EndFor |
| Concatenate A2 andA3 and transfer to A4 |
| For i = 0 to 7 |
| A4[i]=A2[i] |
| EndFor |
| For i =o to 7 |
| A4[i+8]=A3[i] |
| EndFor |
| Right circular shift level-one cipher text block in Array A4 using sub-key ks4 |
| For n=0 to ks4 |
| For i=15 to 0 |
| A4[i+1]=A4[i] |
| EndFor |
| A4[0]=A4[16] |
| EndFor |
| Code. 6, Transposition of level-one cipher text characters in a block using Arrays |
| After this operation, the contents of A4represent the cipher text characters in a given block. The elements of array A4 are moved to the cipher text block C(0) through C(15). The transfer operation is shown in code. 7. The cipher text blocks are used to create the output cipher text message file. |
| For i = 0 to 15 |
| C[i]=A4[i] |
| EndFor |
| Code.7: Transferring transposed level-one cipher text characters to ciphertext block. |
| The Decryption Process. |
| The decryption algorithm performs the reverse operations of encryption such that P = D(K,C). It is done in three steps. Here, cipher text character C(i), in blocks of 16 are processed using arrays and ma t r i . In the decryption algorithm, sub-keys are generated from the secret key in the same way as in the case of the encryption algorithm. |
| Step 1.Initial Matrix Structure. |
| An identical matrix M, used for mapping the plaintext characters into level-one cipher text characters, is used here for inverse mapping of the level-one cipher text characters into plaintext characters during decryption. At the decryption site, this matrix is created using the secret key K in the same way as in the case of encryption. |
| Step 2. De-transposition of ciphertext characters using arrays. |
| Refer to code. 8 which show the de-transposing operation performed on cipher text characters using circular shift appl ied on ar rays in the opposi te directions. The de-transposing operation converts C[i] to CL1[i]. |
| // Transfer cipher text block to Array A4 |
| For i = to 15 |
| A4[i]=C[i] |
| EndFor |
| // Left circular shift level-one cipher text block in Array A4 using sub-key ks4 |
| For n = 0 to Ks4 |
| A4[16]=A4[0] |
| For i= 0 to 15 |
| A4[i]=A4[i+1] |
| EndFor |
| EndFor |
| // Transfer half of Array A4 to Array A2 and left circular shift using sub-key ks2 |
| For i = 0 to 7 |
| A2 [i] = A4[i] |
| Endfor |
| For n =0 to ks2 |
| A2[8] =A2[0] |
| EndFor |
| For i =0 to 7 |
| A2[i]=A2[i+1] |
| EndFor |
| //Transfer other half of Array A4 to Array A3 and right circular shift using sub-key ks3 |
| For i = 0 to 7 |
| A3[i]=A4[i+8] |
| EndFor |
| For n=0 to ks3 |
| For i=7 to 0 |
| A3[i+1]=A3[i] |
| EndFor |
| A3[0]=A3[8] |
| EndFor |
| //concatenate A2and A3 i into A1 |
| For i = 0 to 7 |
| A1[i]=A2[i] |
| EndFor |
| For i =0 to 7 |
| A 1[i + 8] = A3[i] |
| EndFor |
| // Left circular shift level-one cipher text block in Array A1 using sub-key ks1 |
| For n = 0 to Ks1 |
| A1[16] = A1[0] |
| For i = 0 to 15 |
| A1[i]=A1[i+1] |
| EndFor |
| EndFor |
| //moving de-transposed cipher text characters in a block to level-one cipher text block using arrays |
| For i = 0 to 15 |
| CL1[i]=A4[i] |
| EndFor |
| Code8: De-transposition of cipher text characters in a block using |
| The cipher text characters, c[0] through c[15], in a text block are transferred to a 16 elements array A4.This array is left circular shifted as many number of times as equal tio the integer value of key Ks4.after this operation the first eight elements are shifted to another array A2 having eight elements then this array is left circular shifted as many number of times as equal to the integer value of key Ks2.The other eight elements of the array A1 are shifted to the array A3 which is right circular shifted as many number of times as equal to the key Ks3 then the contents of the array A2 and A3 are concatenated into the array A1 having 16 elements .then array A1 is left circular shifted as many number of times as equal to the integer value of key Ks1. |
| After this operation the contents of the array A1correspondas to the level-one cipher text characters block corresponding to the one obtained after the mapping operation done at the encryption side using the matrix. |
| Step 3.Inverse Mapping Using the Matrix |
| If cL1[i] is the level-one cipher text character in the block, the inverse mapping is done such that P[i]=char((column no. j of ith row matrix M where cL1[i] is the element)+32). For example, let the 1st level-one cipher text character, Cl1[1],in a block be ?#‘ .we proceed to search # in the matrix M to find the column no. j in the 1st row where cL1[1]=m[1][j]. Then we determine the character the whose ASCII =(j+32) which gives the plaintext character P[1] corresponding to cl1[1].in this way we can inverse map every ciphertext character in every block into plaintext characters to get back the original message file. |
| Code9. inverse mapping of level one cipher text characters into the plaintext characters using matrix M. |
| For i=0 to 15 |
| J=0 |
| While cL1[i] not equal to M[i][j] |
| J=J+1 |
| EndWhile |
| P[I]=characters whose ASII is (j+32) |
| EndFor |
IV. CONCLUSION
|
| The proposed symmetric encryption technique has two most significant advantages over traditional schemes based on Feistel ciphers. First, the Encryption and decryption procedures are much simpler, and consequently much faster. Second, the security level is higher due to the inherent poly-alphabetic nature of the substitution mapping method used in the encryption process and the transpose operations performed after a level one cipher text generation. |
| |
Figures at a glance
|
 |
| Figure 1 |
|
| |
References
|
- Kilian .J, Phillip ,Rogaway ?How to protect DES against exhaustive key search?, Advances in Cryptology - Crypto '96, Springer-Verlag, pp. 252–267,1996
- Thomas B.E, Serge .V, ?Proving the Security of AES Substitution-Permutation Network?, 12th International Workshop, SAC 2005, vol. 3897, p. 65-81,2005
- William C Barker,?Recommendation for the TripleData Encryption Algorithm(TDEA) Block Cipher?,IJCSAC,2005.
- El-Ramly, S.H. El-Garf, T. Soliman, A.H., ?Dynamic generation of s-boxes in block cipher systems?: CryptoScience Conference, Proceedings ofthe Eighteenth National Publication ,Volume: 2, page(s): 389-397,2003
- 5. Elena C. Laskari, Gerasimos C. Meletiou and Michael N. Vrahatis, ?Utilizing Evolutionary Computation Methods for the Design of S-Boxes?,Federal InformationProcessing Standards Publication 197 November 26, 2001.
- Announcing the Advanced Encryption Standard (AES), Federal Information Processing Standard Publication197,November 26, 2001.
- Juan Soto and Lawrence Bassham, ?Randomness Testing of the Advanced EncryptionStandard Finalist Candidates?, Computer Security Division,National Institute of Standards and Technology, March 28, 2000
- Susan landau ?communications security for the twenty-first century:the advanced encryption standard? the notices of the AMS,volume 47,no.4,apr2000.
- SchneierB.,?Fast Software Encryption? , Cambridge Security Workshop Proceedings (December 1993), Springer-Verlag, 1994, pp. 191-204,1993
- AameerNadeem , Dr. M. YounusJaved " A performance analysis of of data encrption standard ", 0-7803-9421-6/2005 IEEE.
- Susan Landau ?Standing the Test ofTime: The DataEncryption Standard?, Notices of the AMS march ,Vol47,No.3 ,MARCH2000.
- Carolynn Burwick, Don Coppersmith, Edward D.Avignon, ?The MARS Encryption Algorithm?,CiteSeer,1997.
- Ronald L. Rivest1, M.J.B. Robshaw2, R. Sidney2, and Y.L. Yin2, ?The RC6 Block Cipher? M.I.T. Laboratory for Computer Science report, pp 20-30, 1998.
- Bruce Schneier, John Kelsey, Doug Whiting, David Wagner, Chris Hall, NielsFerguson“TwofishA 128-Bit Block Cipher?,CiteSeer,1998.
- Ross Anderson1,EliBiham, Lars Knudsen, ?Serpent: A Proposal for the Advanced Encryption Standard?2000.
- Christophe De Canniere , Alex Biryukov and Bart Preneel " An introduction to block crypt Analysis " proceedings of the IEEE,vol 94,no.2,2006.
- PriyaDhawan, ?Performance Comparison: Security Design Choices?,Microsoft Developer Network,October 2002.
- Schneier B., ?Description of a New Variable-Length Key, 64-Bit Block Cipher (Blowfish)?Fast Software Encryption, Cambridge Security WorkshopProceedingSpringer-Verlag, pp. 191-2041994.
|