Keywords
|
| Automatic generation control, conventional controllers, reheat turbine, sampling time period, Fuzzy Controller. |
I. INTRODUCTION
|
| The objective of control strategy is to generate and deliver power in an interconnected power system as economically and reliably as possible while maintaining the voltage and frequency within specified limits. Changes in real power affect mainly the system frequency, while reactive power is less sensitive to changes in frequency and is mainly dependent on the changes in voltage magnitude. Thus, real and reactive powers are controlled separately. |
| The load frequency control (LFC) loop controls the real power and frequency and the automatic voltage regulator (AVR) loop regulates the reactive power (Q) and voltage magnitude (V). Load frequency control (LFC) has gained the importance with the growth of interconnected power system and has made the operation of the interconnected power system possible. The objective of the Automatic generation control is to hold the system frequency at or very close to a rated nominal value (eg.50 Hz), to maintain the correct value of interchange power Between control area and to maintain unit generation at the most economic value. |
| Automatic generation control means closed loop control systems which hold the system frequency within target limit. It also maintains the power interchange between adjacent system through tie lines.AGC helps generation of each plant within the area at economical value. The automatic generation controller design with better performance has received considerable attention during the past years and many control strategies have been developed for AGC problem. The availability of an accurate model of the system under study plays a crucial role in the development of the most control strategies like optimal control. However, an industrial process, such as a power system, contains different kinds of uncertainties due to changes in system parameters and characteristics, loads variation and errors in the modelling. On the other hand, the operating points of a power system may change very much randomly during a daily cycle. The major part of the work reported so for has been performed by considering linearized models of two/multi area power systems [1, 4- 8]. The effect of GRC was included in these types of studies, considering both continuous and discrete power system models [9-10]. It has been already illustrated that supplementary controller designs based on tie line bias control strategy is caused that he ACEs is regulated to zero effectively. |
II. PROPOSED FUZZY LOGIC CONTROLLER
|
| It has the capability of simulating human decision making based on fuzzy concept implications and the rules of inference in fuzzy logic. The knowledge based of an FLC is comprises of two components, a database and fuzzy control base. The concepts associated with a data base are used to characterize fuzzy control rule and a fuzzy data manipulation in a FLC.the design of a novel AGC controller based on fuzzy logic theory is explored. With the goal of damping the oscillations associated with power systems under the effect of small signals in local modes must be damped. The proposed solution of this problem is that a fuzzy controller is to be developed based on the optimal control theory. |
| Fuzzy logic is a thinking process or problem-solving control methodology incorporated in control system engineering, to control systems when inputs are eitherimprecise or the mathematical models are not present at all. Fuzzy logic can process a reasonable number ofinputs but the system complexity increases with the increase in the number of inputs and outputs, therefore distributed processors would probably be easier to implement. Fuzzification is process of making a crisp quantity into the fuzzy. They carry considerable uncertainty. If the form of uncertainty happens to arise because of imprecision, ambiguity, or vagueness, then the variable is probably fuzzy andcan be represented by a membership function |
Normalization
|
| Normalization performs a scale transformation and it’s also called input Normalization. It maps the physical values of the current process state variable into normalized universe of discourse. It also maps the normalized value of control output variable into physical domain. For this controller, normalization is got by dividing each crisp input to the upper boundary values for the associated universe. |
Fuzzification
|
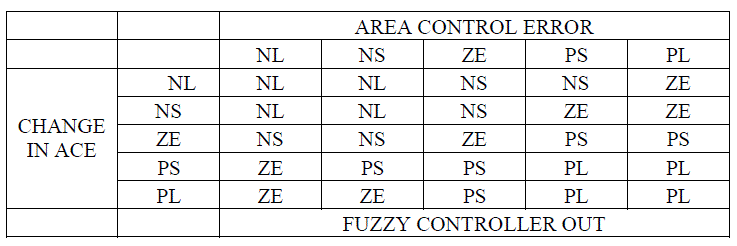
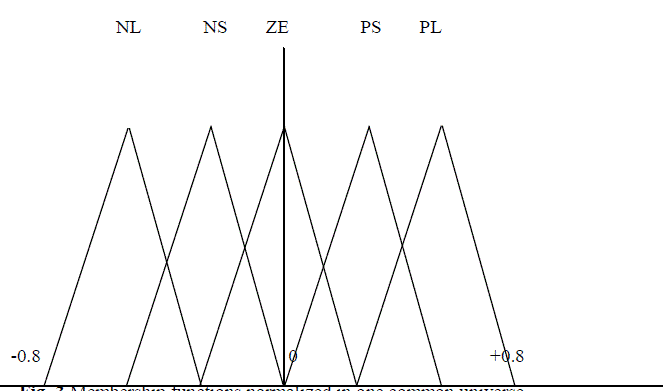
| Fuzzification is the process of changing the crisp valve to the fuzzy values. It could be defined as a mapping from an observed input space to fuzzy sets in certain input universe of discourse. Fuzzification plays an important role in dealing with uncertain information, which might be objective (or) subjective in nature. In fuzzy control applications, the observed data are usually crisp since the data manipulation in an LFC is based on fuzzy set theory. Fuzzification is necessary during the earlier stage. The choice of membership function for each Linguistic variable must be performed. This can be done by classification of control input and output into classified fuzzy set as shown in Figure 3. |
The ACE and change in ACE are classified into:
|
| {Negative Large (NL) , Negative Small (NS) , Zero (ZE) , Positive Small (PS) , Positive Large (PL)} |
III. SYSTEM INVESTICATED
|
| Both active and reactive power demands are never steady and they continually change with the rising or falling trend. Steam input to turbo-generators (or water input to hydro-generators) must, therefore be continuously regulated to match the active power demand, falling which the machine speed will vary with consequent change in frequency which may be highly undesirable (maximum permissible change in power frequency is + 0.5 Hz). Also the excitation of generators must be feasible Both active and reactive power demands are never steady and they continually change with the rising or falling trend. Steam input to turbo-generators (or water input to hydro-generators) must, therefore be continuously regulated to match the active power demand, falling which the machine speed will vary with consequent change in frequency which may be highly undesirable (maximum permissible change in power frequency is + 0.5 Hz). Also the excitation of generators must be feasible |
III. RESULT & DISCUSSION
|
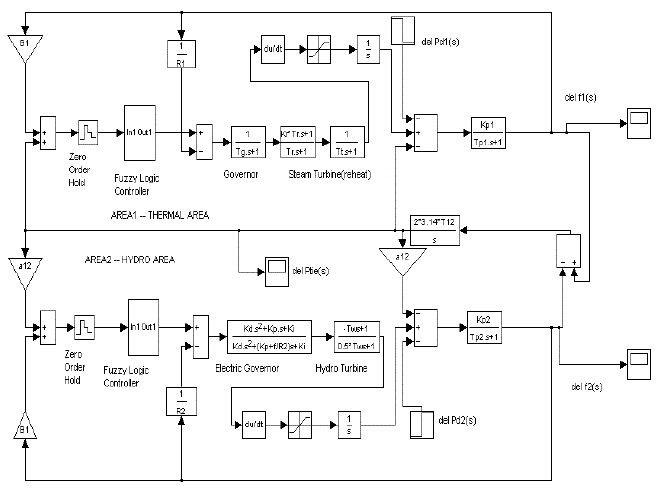
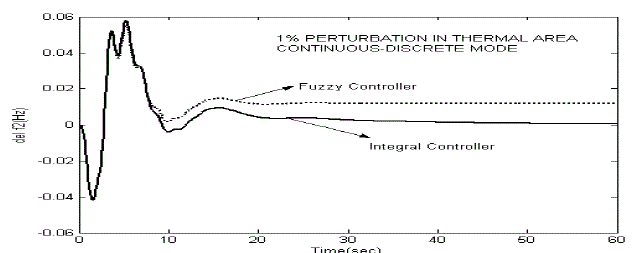
| From the comparison of integral controllers and fuzzy logic controllers for the 1% step load perturbation, we can conclude that the fuzzy logic controller is better. The settling time of fuzzy logic controller is less where as the settling time for the convention integral controller is more as compared to fuzzy logic controller. With the new technique such as fuzzy logic controllers, it is easy for controller setting corresponding to the small frequency deviation and tie-line power deviation due to the small step load perturbation. Fig 4 (a). Dynamic response with 1% perturbation in thermal area. |
V.CONCLUSION
|
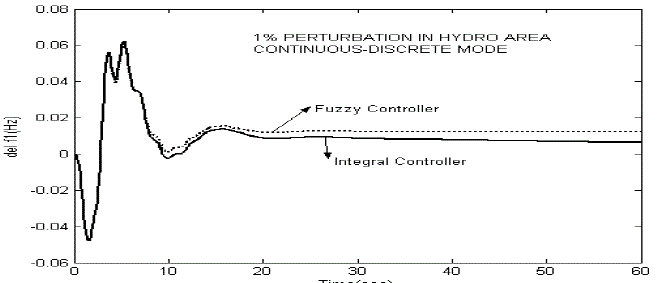
| Thus from the table-I to table-II, we can conclude that fuzzy logic controller has good dynamic responses in overall closed loop system. From the dynamic response analysis, the fuzzy logic controller has found to provide better suppression of oscillations and also better damping of peak over shoot in same of the operating conditions. As compared to the conventional integral controller and fuzzy logic controller, in fuzzy logic controller provides fast and better responses. And the settling time and peak overshoot is less as compared to the conventional integral controllers. This comparison is made by considering 1% step load perturbation in both thermal and hydro area. |
| |
Tables at a glance
|
 |
 |
| Table 1 |
Table 2 |
|
| |
Figures at a glance
|
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
 |
 |
 |
| Figure 4 |
Figure 4a |
Figure 4b |
|
| |
References
|
- Janardan Nanda, Ashish Mangla and Sanjay Sui, “Some New Findings on Automatic Generation Control of an Interconnected Hydrothermal. System With Conventional Controllers” IEEE trans, Vol.21, No.1, March 2006.
- J. Nanda and A. Mangla “Automatic Generation Control of an Interconnected Hydro-Thermal System Using Conventional Integral and Fuzzy LogicController” IEEE tans, April 2004.
- O. I. Elgerd and C.E. Fosha, “Optimum megawatt-frequency control of multiarea electric energy system,” IEEE tans. Power Apparat. Syst., Vol.25,No.10, pp. 1063-1077, December 1997.
- O. I. Elgerd, Electric Energy Systems Theory, New York: McGraw-Hill, 1971, pp.315-389.
- C. Concordia and LK.Kirchmayer, “Tie-line power & frequency control of electric power system: Part II, ” AISE Trams. III-A, vol.73, pp.133-146,April 1954.
- L. K. Kirchmayer, Economic Control of Interconnected Systems. New York: Wiley, 1959.
- D. G. Ramey and J. W. Skooglund, “Detailed hydro governor representation for system stability studies,” IEEE Trans. Power App. Sust., vol. PAS-89, no.1, pp. 106-112, January 1970.
- “IEEE Trans. Power Apparat. Syst., ” IEEE Committee Rep., vol. PAS-86, pp.384-395, 1966.
- M. L. Kothari, J. Nanda, and P. S. Satsangi, “Automatic generation control of hydrothermal system considering generation rate constraint,” J. Inst.Eng. India, vol.63, pp.289-297, June 1983.
- M. L. Kothari, J. Nanda, and B. L. Kaul “Automatic generation control of hydrothermal system,” J. Inst. Eng. India, pt EL2, vol.61, pp.85-91, October1980.
|