International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Integrated Topology Control and Routing Problem in Cluster-Based Wireless Sensor Networks

M.Jenora 1, A.Anto Jenifer 2, D.Anitha 3
  1. P.G. Student, Department of Computer Engineering, Govt. College of Engineering, Tirunelveli, Tamilnadu, India
  2. P.G. Student, Department of Computer Engineering, Govt. College of Engineering, Tirunelveli, Tamilnadu, India
  3. Associate Professor, Department of Computer Engineering, Govt. College of Engg, Tirunelveli, Tamilnadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Data-gathering wireless sensor networks (WSNs) are operated unattended over long time horizons to collect data in several applications. Typically, sensors have limited energy (e.g., an on-board battery) and are subject to the elements in the terrain. In-network operations, which largely involve periodically changing network flow decisions to prolong the network lifetime, are managed remotely, and the collected data are retrieved by a user via internet. An integrated topology control and routing problem in cluster-based WSNs are analyzed to improve the network lifetime. To prolong network lifetime via efficient use of the limited energy at the sensors , a hierarchical network structure with multiple sinks at which the data collected by the sensors are gathered through the cluster heads are adopted . A Mixed Integer Linear Programming (MILP) model to optimally determine the sink and CH locations as well as the data flow in the network is considered. This model effectively utilizes both the position and the energy-level aspects of the sensors while selecting the CHs and avoids the highest-energy sensors. For the solution of the MILP model, an effective Benders Decomposition (BD) approach that incorporates an upper bound heuristic algorithm is used.

Keywords
Benders decomposition (BD), network design, wireless sensor networks (WSNs).

INTRODUCTION
The general framework of WSN network operations of our interest can be outlined as follows. Initially, a set of sensors, which are equipped with limited energy resource (e.g., battery) as well as sensing, processing, and communication capabilities, is deployed in a geographical region. Data collected by the sensors are forwarded to specially designated sensors, called cluster heads (CHs), which conduct some processing to aggregate their received data. CHs then forward the data to specific locations, called sinks, either directly or through other CHs. 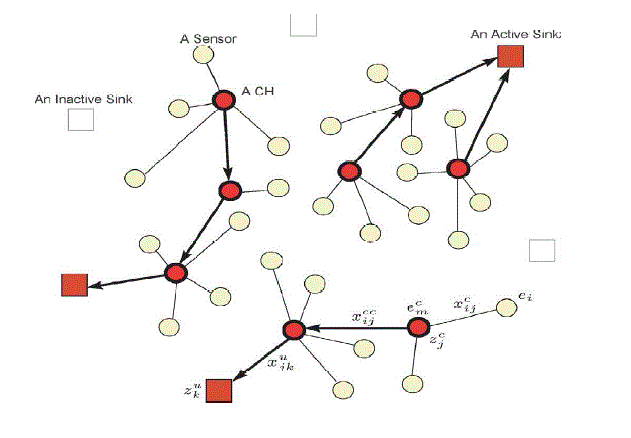In this underlying setting, which is also depicted in Fig. 1, design of the network refers to the determination of CH and sink locations, while the operation decisions refer to the routing of data from the sensors to the sinks in that network
Given limited energy levels at the sensors, as is the case in many applications of WSNs, one of the main concerns in network design and operation is the network lifetime, which we consider in this study to be the time between two sensor deployments. Sensor redeployments may be needed due to several reasons, e.g., having less than a critical number of operational sensors with enough remaining energy in the network
Typically, the lifetime is assumed to be divided into periods of uniform length, and for each period, network design and operations decisions are made in such a way that the number of periods in a deployment cycle is maximized. Consequently, the network lifetime is defined as the number of periods that can be achieved with a deployment
Topology control and routing are two fundamental problems in effective design and operation of WSNs. The close relationship between these decisions and their relation to network lifetime are especially underlined by the WSNspecific design/operation attributes that include energy efficiency and computation–communication trade-off. As mentioned, energy efficiency is a major concern since each sensor has finite and on renewable energy resource Communication–computation trade-off refers to the fact that communication consumes more energy than performing computations on board a sensor.
This is critical as it relates to the energy efficiency. Although the direct communication of a sensor with a sink is preferable for the overall network, this is impractical or, otherwise, leads to excessive energy use, thus shortening the network lifetime. Therefore, routing schemes where the data size is decreased via in-network data aggregation (i.e., using energy for computation rather than communication) along the paths from sensors to a sink (user) are usually preferred.

II. RELATED WORK
In this section, we will see the some of the related works to network topology and data routing: Heinzelman et al. [2] develop a data aggregating cluster-based routing protocol Low Energy Adaptive Clustering Hierarchy (LEACH). In LEACH, they assume a single-hop CH-to-sink connection and adopt the randomized rotation of CHs to ensure balanced energy consumption. However, such assumptions may not guarantee network connectivity.
Younis and Fahmy [26] propose a hybrid energy-efficient distributed clustering routing (HEED) protocol where the CHs are probabilistically selected based on their remaining energy and the sensors join clusters such that the communication cost is minimized. HEED assumes a multihop connection between the CHs and to the sink
Liu et al. [3] suggest a distributed energy-efficient protocol EAP for the general setting in [26]. In EAP, each CH is probabilistically selected based on its ratio of the remaining energy to the average remaining energy of all the neighbor sensors within its cluster range. This is in contrast to HEED that only chooses CHs based on a sensors’ own remaining energy. To further extend network lifetime, EAP introduces the idea of “intracluster coverage” that allows a partial set of sensors to be active within clusters while maintaining an expected coverage
Ademola et al. [27] also aim to promote a uniform energy usage across the network by minimizing the communication distance among sensors and selecting the CHs based on remaining energy at the sensors. Since sensors generally send data to the sink in a “many-toone” (convergecast) fashion, Haenggi [23] points out that some critical sensors closer to the sink appear on most forwarding paths in the network. Specifically, in a multihop cluster-based WSN, the CHs closer to the sink may have quick drainage due to their heavy load in forwarding data to the sink
In contrast to the above studies that adopt a localized and/or protocol-based method, Al-Karaki et al. [27] present a mathematical formulation by jointly considering the cluster-based routing problem with application-specific data aggregation
Al-Turjman et al. [15] propose a mixed integer linear program (MILP) with the objective of minimizing the total network energy consumption while including constraints on fault tolerance simultaneously. In that study, sensors are assumed to forward their data to the sink through specific relay nodes that are equipped with higher energy sources. In [4], a routing problem is considered for networks with flat topologies. For this, a linear programming approach is suggested to maximize the data flow per period. In another study, with similar assumptions but without considering data aggregation, a multicommodity flow approach is provided to maximize lifetime with the use of multiple sinks in a WSN.
Wang et al. [5] also consider a similar setting with mobile CHs that are special high-energy sensors and examine the network lifetime under fixed sink location assumption. Efforts toward that end also include consideration of placing specific relay nodes with more energy .
Kim et al. [15] illustrate the benefit of employing multiple sinks and suggest a mixed integer linear program to determine sink locations. Luo and Hubaux [30] address a routing problem with sink mobility to improve network lifetime. Efficient approximation algorithms for generation of multihop routing trees (single sink) and forests (multiple sinks) are provided in [6]. However, in these studies, flat-routing structures without any CHs or aggregation are considered.
In our specific context of cluster-based approaches, we have the following observations: 1) Most of the studies in the clustered sensor network adopt a localized method to select and vary CHs over the periods. Such methods may be biased from the long-term network lifetime perspective. 2) In the majority of the literature, topology control and routing problems are handled separately, thus overlooking the interrelationships among them. 3) The majority of studies on cluster-based WSNs does not consider the use of multiple sinks with mobility. Therefore, we are motivated to investigate a generalized and integrated topology control and routing problem using optimization techniques. In doing so, we particularly consider a multiobjective optimization model that combines energy usage and remaining energy characteristics and that simultaneously considers cluster-based topology control and routing decisions in a multiple-sink WSN having a hierarchical network structure to facilitate data aggregation
For our mathematical model, we develop a solution algorithm based on joint use of Benders decomposition and an effective heuristic and analyze both algorithmic and network characteristics in an extensive computational study.

III. PROPOSED WORK
To prolong network lifetime through use of the limited energy at the sensors, we adopt a hierarchical network structure with multiple sinks at which the data collected by the sensors are gathered through the ClusterHeads (CH). We consider a Mixed Integer Linear Programming (MILP) model to determine the sink and CH locations and the dataflow in the network. An upper bound heuristic algorithm is used to incorporate Benders Decomposition (BD) approach
• First, in the modelling context, we incorporate a total fixed cost term associated with CH selection into the objective function. By setting a higher fixed cost of usage (as a CH) for a sensor with low energy, the model attempts to avoid some well-positioned sensors from being selected as CHs repeatedly in successive periods and to protect these sensors from quick energy depletion. This approach also facilitates a uniform energy consumption profile at the sensors across the network. This is important because in a hierarchical setting, where data flow from sensors to the sinks occurs via CHs, a CH not only functions to capture information in its vicinity, but also as an aggregator/relay node to process and transfer the data generated by other sensors to the sinks. Thus, CHs consume more energy than regular sensors, while the whole network operation enjoys taking advantage of the computation–communication trade-off
• Second, observing that the model is amenable to exact solution via Benders decomposition (BD), in the methodological context, we focus our efforts on devising an efficient BD Algorithm as a solution method. In particular we develop a solution approach that incorporates an effective heuristic algorithm and strengthened Benders cuts in an - optimal BD framework. Computational evidence demonstrates the efficient performance of the approach in terms of solution quality and time. In particular, our heuristic algorithm provides a good initial upper bound and facilitates the generation of initial Benders cuts, while the strengthened Benders cuts and -optimal framework accelerate the convergence of the BD algorithm.

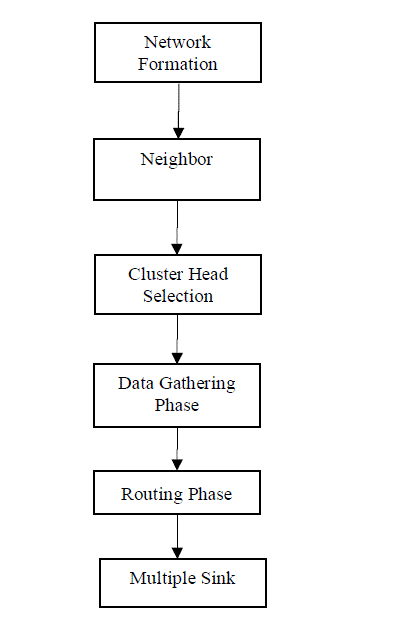
Network Formation
The hierarchical network formation process done by each and every node in the network is grouped either tree, mesh structure. In the structure each and every node having different location, size and energy. The initial energy is given to each node. The distance between the two nodes should be same; if the node0 to node1 distance is 173.8763 then the distance between the node1 to node0 is same value

Neighbor Discovery
This is the process of calculate the neighbor node value and find the surrounding node. The neighbor list is maintained by all of nodes in the network. Each and every node has initial energy value by its creation time. A network describes a collection of nodes and the links between them. The nodes automatically calculate the neighbor nodes depending on transmission power and location of the node using AODV routing protocol.

Cluster head Formation
A CH is a sensor node that transmits an aggregated sensor data to the distant base station. At the start, a set of cluster heads are chosen on random basis. These cluster heads send a message to neighbor nodes and determine which node has high energy. The sensor nodes receive the messages and choose their cluster heads based on the energy that is battery power. Each sensor node sends an acknowledgment message to its cluster head. On cluster heads are sensor nodes that transmit the collected data to their cluster head. Each cluster has a head set that consists of several virtual cluster heads; however, only one head set member is active at one time

Data Gathering Phase
During data gathering phase, the initial part of the data gathering the nodes are in the active state. The nodes are involved in sensing and in the collection of data. After this each node forms a single data packet of its own. Then, the nodes transmit messages to their cluster head and cluster heads transmit an aggregated messages to a distant base station i.e., the information’s are gathered by the sensor nodes and the information’s are sent to the cluster head.

Routing Phase
During the routing phase, each cluster head has the collected data, the cluster head identify whether any other cluster head having more energy. If any highest energy cluster heads are found the information’s are sent that highest energy cluster head ,the heuristic algorithm is used to perform the data transmission to cluster head until reach the highest energy cluster head.

Multiple Sinks
Basically sensors have limited energy. The cluster head sends the information to store in multiple sinks to reduce the energy consumption because if all the data’s are stored in single sink or base station it takes more energy so that multiple sinks are used to increase the network life time securely erasing any ephemeral values used, the access control is still ensured by a cryptographic mean instead of relying on some server to restrict the accesses honestly

IV. APPROACH
Benders Decomposition
Benders decomposition is a solution approach for mixed integer linear programming problems and it has been successfully employed for solving a wide array of large-scale optimization problems. This technique is based on the idea of exploiting the special structure of the problem at hand; it separates the original formulation into two smaller easier-to-solve problems called a master problem and a subproblem.
The master problem accounts for all the integer variables and the associated portion of the objective function and the constraints of the original problem. It also embodies the information regarding the subproblem portion of the problem via use of an additional (continuous) auxiliary variable and a set of constraints called Benders cuts. On the other hand, the subproblem includes all continuous variables and the associated constraints in the original problem. Solving the dual of the subproblem provides information about the subproblem portion of the original objective function, and this information is communicated to the master problem via Benders cuts.

A. Base Benders Decomposition Approach
In each iteration of Benders algorithm, the master problem is resolved to optimality with the addition of a Benders cut. This gives a lower bound for the original problem (P), and values for the integer variables are then substituted into the subproblem. The dual subproblem is then solved to produce an upper bound for (P) and a set of dual variables values that are used to generate a new Benders cut for the master problem in the next iteration.This process is repeated until a termination condition, usually a small optimality gap between the lower bound and the upper bound, is met. In Benders approach, it is known that if the iterations are allowed to continue long enough, an optimal solution is obtained as the Benders cuts recover the complete feasible polyhedron of the overall problem.

B. Benders Subproblem and Its Dual
The subproblem can easily be obtained from the overall formulation (P). Intuitively, for given binary variables associated with fixed CH and sink locations whose locations are known as dictated by the master problem, the subproblem is essentially a linear minimization problem that determines the data routing scheme from sensors to sinks via CHs and energy usage/status in the network.In the Benders framework, rather than solving the subproblem (primal), we solve its dual.

C. Benders Master Problem
The master problem is obtained from the overall formulation (P) by adopting the requirements on the number of CHs and sinks given by constraints. The real-valued variable is contained in the set of Benders. The master problem is essentially a minimization problem that gives a tentative network configuration, selection of CH and sinks locations, and a lower bound of the original model. At each iteration, we obtain a new dual solution , substitute it into constraint , add it to the master problem , and then resolve the master problem to obtain a new set of values of the binary variables

D. Approaches for Accelerating the BD Algorithm
We observe that the direct implementation of classical BD approach in our model often converges slowly. This is due to the following reasons.
1) In the absence of a set of dual variables, BD approach starts the iterative procedure by solving the master problem without any Benders cuts . However, the initial selection of cuts can have a profound effect upon the performance of Benders algorithm
2) Due to the degeneracy of the subproblem, there exist multiple dual optimal solutions for dual sub problem .This means that multiple sets of dual values are possible to provide the same optimum solution to the dual sub problem. Thus, it is important to obtain an optimal solution to so that a stronger cut of the form (30) is generated.
3) The master problem must be solved each iteration a new Benders cut is added Thus, as the number of iterations increases, the complexity and the size of increases dramatically, and, consequently, solving becomes very timeconsuming. In order to circumvent these difficulties, we explore several techniques to accelerate the convergence of the BD algorithm.
E. Upper Bound Heuristic Algorithm: We devise an efficient heuristic algorithm, called Upper Bound Heuristic (UBH),that provides a feasible solution to overall problem (P) without much computational effort. The aim of our heuristic algorithm is to find a good upper bound and facilitate the generation of good initial Benders cuts. We use the solution, specifically CH and sink selections given by , obtained from the heuristic as an input and solve the dual sub problem for generating an initial Benders cut so that it can be added to the master problem in the following iteration. This is in contrast to initially solving the master problem without any cuts in a typical BD implementation. We design the heuristic in a way to avoid well-positioned sensors being selected as CHs repeatedly in successive periods and to protect low-energy sensors from being selected as CHs.

V. CONCLUSION
The results of our proposed hierarchical cluster based routing protocol indicate that the energy consumption can be systematically decreased by including more sensors in a cluster head. For the same number of data collecting sensor nodes, the number of control and management nodes can be adjusted according to the network environment. We develop an MILP model to determine the multiple sink and CH locations and data flow in the network. Our model avoids some well-positioned sensors being selected as CHs repeatedly in successive periods to protect low energy sensors from quick energy depletion while facilitating a uniform energy consumption profile in the network.

Figures at a glance
Figure 1 Figure 2
Figure 1 Figure 2
 

References