ISSN:2321-6212
ISSN:2321-6212
1Biomaterials Laboratory, Instituto Militar de Engenharia, Rio de Janeiro, Brazil
2Instituto Nacional de Pesquisas Espaciais, São José dos Campos - SP, 12227-010, Brazil
Received Date: 02/03/2018; Accepted Date: 11/05/2018; Published Date: 20/05/2018
DOI: 10.4172/2321-6212.1000220
Visit for more related articles at Research & Reviews: Journal of Material Sciences
Standard specifications for orthopedic devices that are implanted in the human body include requirements for materials, finishing, marking, care and handling, but do not address the mechanical properties required for each type of implant. Insufficient mechanical strength is the cause of failure of medical devices. For the development of any implantable device, manufacturers demand information about the load to which the device will be subjected. In the case of fracture fixation, information is often missing. This review presents relevant information regarding biomechanics and common loads, moments and stress related to the intrinsic relation between human bones during daily activities. Results that arose from these calculations are expected to be stood by medical devices when outlined for stabilization of bone fractures
Bone loading, Physiological loading, Medical devices, Human bone
Material selection based on technical standard requirements is not sufficient to ensure the good performance of medical devices; the design and the manufacturing process can strongly influence the device properties. It is not the intention of technical standard to define levels of performance of any medical implant. It is the responsibility of the manufacturer to establish appropriate safety and health practices and determine the applicability of regulatory limitations prior to use an implant. The mechanical test method is used only for purposes of assuring the homogeneity of the production. Based on standard specifications, the essential quality and regulatory requirements, such as safety, and dependability of any implant are established by the manufacturer during the design and development phase. Faulty design and inadequate material specification can be a cause of quality problems and failure of medical device. Despite ever-increasing literature on medical device failures analyses, there are no authoritative and evidence-based guidelines for the management of orthopedic fracture fixation. A general lack of consensus exists among orthopedic trauma surgeons and implants manufacturers on the management of these fractures failures. Design validation should ensure that the implant will meet the patient needs and should specify the conditions for approval in tests that simulate daily use.
Bone strength depends on bone density, geometry, composition, morphology, patient age, sex and patient activity. In most cases, bone fracture produces a mechanical instability that hinders the healing process. The mechanical effect induced by a fracture consists primarily of a loss of bone continuity, resulting in pathological mobility and loss of bone support [1]. This traumatic discontinuity ruptures blood vessels around the bone and releases agents that promote bone healing. Thus, although fracture is a purely mechanical process, it initiates important biological reactions such as bone resorption and bone formation. For bone remodeling to occur, it is very important that the two sides of the fracture are correctly aligned. Mistreated fractures may stabilize in a condition that impairs motor function.
In the treatment of bone fractures, a procedure to restore the alignment and facilitate the healing process of the limb may be characterized as providing absolute or relative mechanical stability. Rigid implants are intended to reduce the mobility of the fracture. Flexible surgical fixation of the fracture with plates or rods allows micromotion between the fracture fragments under stress. Fracture consolidation under flexible or unstable condition typically occurs by formation of a callus that mechanically unites bone fragments. The only technique that restricts the motion at the fracture site is interfragmentary compression [2]. Stability reduces the stress at the fracture site and allows healing without the formation of visible bone callus.
Biomaterial selection for implants, plates and screws is based on mechanical properties, biocompatibility and ability to perform the desired function. In order to determine the dimensions of these devices one should know the mechanical properties of the chosen materials and the intensity of the forces to which the bone fracture region will be submitted. The literature provides the necessary data of physiological bone loading in the human head (mandible, maxilla, teeth, skull and middle third of the face) for the development of products used in fracture fixation in the bucomaxillofacial region [3]. The purpose of the present study is to collect similar data for the human upper limb region (shoulder, arm, forearm and hand), lower limbs (hip, femur, tibia, foot and tendons) and vertebral column (cervical, thoracic and lumbar spine).
Figures 1-5 show the regions that were investigated in the present work. Knowledge of these loads is important for the design and development of new orthopedic devices, such as implants, plates and screws. These devices are used in bone healing, osteosynthesis, functional replacement of a portion of the bone, surgical reconstruction and to support initial loading during arthrodesis. This work should be considered useful for students, researchers, engineers and medical device manufacturers involved with the development and production of implants used in orthopedic fracture fixation.
Shoulder
The shoulder complex is composed by four joints in direct relation to scapula, clavicle, sternum and first rib. All joints act together and interact during any significant movement of the arms [4,5]. The connection of the clavicle to the scapula is established by the acromioclavicular joint and anatomically host a fibrocartilaginous disc, that contributes to handle the large amounts of stresses transmitted through this joint during most of the movements of the scapula [6].
The connection of scapula with thorax is set up by the scapulothoracic joint, which allows a smooth connection by interactions among muscular and bursal structures [5,6]. More than seventeen muscles are in close relation to scapula, being attached on or being originate from the large triangle flat topography of this bone. This joint is able to increase the total rotation of the humerus and also facilitates a large lever movement of the different muscles that attach to scapula bone.
One of the reasons for the extreme mobility of shoulder complex is because of the smaller size of the glenoid fossa from the glenohumeral joint when compared to the extension of the humeral head. Based on the limited anatomic contact between the joint socket and the head of the humerus, the stability of the shoulder is dependent on the interactions from the ligamentous and muscular structures attached to the complex [7,8]. The only region of skeletal attachment of the upper trunk is established by the stenoclavicular joint. This joint connects the clavicle to the sternum bone, being the clavicles a strategic structure for muscular attachments, which stabilize and protects underlying areas, while also prevent medial displacement and lower migration of shoulder girdle [6,8,9].
The great mobility of shoulder, mainly in flexion and abduction, results in instabilities in the complex during repetitive joint actions and can result in inflammatory reactions around joints and muscular attachments [6,10]. Trauma is also reported as a consequence of traumas during falls or direct impacts in different areas components of shoulder complex including shoulder girdle, clavicle bone and more rarely in scapula.
The type of shoulder fracture varies by the population age. The most common shoulder fracture in children occurs in the clavicle bone, which frequently result of a fall. The scapula fracture rarely occurs. The most common fracture in adult is of the top part of the humerus (proximal humerus). Many shoulder fractures can be treated with a sling. Some fractures are severe enough and the treatment requires surgery. Some surgeries involve placing plates, pins and screws or wires.
Arm (Humerus)
Figure 1 shows the distribution of forces in the shoulder, arm and forearm. The humerus fits into the shoulder as a ball and socket joint. Humeral shaft fractures comprise 1 to 5% of all fractures [11]. Humeral fractures are managed through conservative treatment or surgery. Plates and screws or intramedullary nailing and external fixation can be used in surgical treatment. The clinical results show that a less rigid fixation promotes secondary bone healing with more callus formation. The best procedure is the use of bridge plating fixation with locking plates, which enable bone micromovements [11].
Ulian et al. [12] evaluated different methods of osteosynthesis in the humerus. Based in their work, the forces acting on the shoulder and their distribution through the arm and forearm are approximately the load to the humerus fracture by flexocompression. For men with 1.70 m and 80 kg, the humerus fracture occurs with 52 N loading. Results of mechanical tests of the bone cylinders from the humeral head showed that the average ultimate strength is from 3.21 MPa to 6.17 MPa.
Dislocation of the shoulder (glenohumeral) joint is common and the return to correct position is easy. Anglin and Pichora [13] studied the glenohumeral contact forces during five activities of daily living: standing up from a chair using the arms (compression in both arm in axial direction), sitting down into a chair using the arms (compression in both arm in axial direction), walking with a cane (compression in one arm in axial direction), lifting a 5.0 kg (49 N) box from the floor to shoulder height using both hands (tensile in both arm in axial direction) and lifting a 10.0 kg (98 N) suitcase using one hand (tensile in one arm in axial direction). Six healthy voluntary with ages ranging from 51 to 64 (mean, 55), bodyweight (BW) from 52 to 89 kg (mean, 73 kg) and height from 1.52 to 1.87 m (mean, 1.68 m) were recruited for the study. The measured forces ranged from 0.3 to 6.9 times body weight. The glenohumeral force for standing up from a chair was 0.5 to 4.3 BW, walking with a cane was 0.4 to 3.2 BW. Sitting down needs the lowest glenohumeral (0.3 to 0.5 BW) and lifting a 10.0 kg box from the floor using both hands was the higher glenohumeral force (1.5 to 6.9 BW). Although the study was realized in the glenohumeral area, it is known that the supported load will be transmitted to humerus as a whole. Using a safety margin of 100%, the value of 1260 kg may be taken as the minimum force required for a medical device.
For an analysis under stress, Gomez and Nahum [14] reported in a study on the geometric properties and stress fracture of long bones that a force of 2840 N is required to fracture the humerus in compression and torsion. For fracture under bending loading, the force is 1.510 N. The ultimate stress of humerus cortical bone is 122.58 MPa. Thus, for an analysis of stress, values of 450 MPa (2 times 123 MPa) may be taken as a criterion for approval of products seeking consolidation of fractures of the humeral region. For approval in torsion, the value of moment of 0.43 N⋅m/degree may be taken for a product aiming at consolidation in the same region.
The Elbow
The elbow establishes connection between the arm (humerus bone) and forearm (radius and ulnar bones) by the interaction of these elements with joints, ligaments and muscles [9]. Forearm movements are dependent of the shoulder force applications, beside participation on the control of the hands during action of wrist and fingers.
There are three joint which compose the elbow system, allowing movements of the bones in arm and forearm. Humerus is connected to the proximal part of ulna and radius bones by the ulnohumeral and radiohumeral joints [15]. An angle between 10- 25° exists between the long axis of humerus and the radioulnar bones during extended position [16]. The last joint interconnects radius and ulna allowing pronation and supination of these bones. The interrelation between them is maintained by an interosseous membrane which also assists in force transmission applied to radius to ulnar bone.
Brodbeck et al. [17] cited that the wrist in a below elbow splint without any load bearing during the time of recuperation would hardly be exposed to a force of 10 N during 1500 to 3000 times per day.
Forearm (Radius and Ulna)
According to Gomez and Nahum [14] the compressive strength of the radius is 950 kg for men and 780 kg for women 20 to 89 years old. The maximum compressive load of the ulna is 1,140 kg for men and 850 kg for women. The average stress required to fracture the radius in bending is from 18.5 ± 0.4 to 23.2 ± 0.6 kg/mm². The ultimate torsional strength of the ulna is 4.95 kg/ mm². This information is important for calculating the dimensions and selecting the implant material.
Approaching the minimum cross section of radius and ulna by a circular cross section, one can calculate the stress corresponding to an applied force of 15 N (weight of hand and forearm), plus a weight 15 kg (150 N) being held at the tip of the arm. Knowing that the stress is given by:
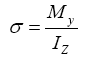 (1)
(1)
the moment to which the farthest point of forearm is subjected can be calculated using the equation.
M=Fd (2)
where F is the applied force (150 N) and d is distance to the point of application.
According to solid mechanics, a continuous stress can be moved to the center of mass to calculate mechanical stress.
Hamill [15] estimated the location of the center of mass of some object. The calculations are related to different studies where a percentile of the total body mass is used to reveal the segment weight of each part of the human body. The location of the center of mass is based on a percent of segment length from proximal-end orientation. In the case of an assembly formed by forearm and hand varies with dimensions of these segments and is located at 0.682L from the proximal end and 0.318L from distal end, where L is the arm length. The ratio between the height H of people and the length of the ensemble formed by forearm and hand is about 0.254H. Assuming a person 1.80 m high, the length of hand and forearm would be 46 cm and the center of mass would be located at 31.2 cm (180 cm × 0.254 × 0.682) from the proximal region, as illustrated in Figure 1. The mass of the forearm and hand as separated parts might be 0.016 and 0.007 percent of the total weight of a male body, respectively. These values might slight vary as 0.0157% and 0.005% if a female body was used as an example.
Another relevant aspect related to the center of mass, is the influence of the mass balance on the axis of rotation of the object. The resistance imposed by the mass on the ability of this object to be moved is called inertia and can be quantified by the moment of the inertia. Nevertheless, there are limitations to calculate the moment of inertia of parts of human body for considerations of these parts as homogeneous bodies since they are composed by several tissues with singular characteristics. Thus, an option could be to consider the parts as unique segments and calculations be executed in terms of the radius of gyration, which consider the mass distribution of each part, separately and correlated its influence based on the axis of rotation where the movement is imposed. Eqn. (3) can be used to estimate the moment of inertia of each segment of human body:
I=m (ρL)² (3)
where I is the moment of inertia of each segment (based on the radius of gyration), m is the mass of the segment, ρ is the radius of gyration and L is the segment length.
Another way to estimate the moment of inertia is to take as reference any parallel axis to the axis that pass through the center of mass of an object. This calculation technique is known as the parallel axis theorem and is resumed by eqn. (4)
Ix=I + mr² (4)
where Ix is the moment of inertia in any parallel axes, I is the moment of inertia took as reference who passes through the center of mass, m is the mass of the object and r is the perpendicular distance between booth axis.
In order to estimate normal loading, we assumed that the ulna supports the weight of 15 kg at the tip of the arm. Since the center of gravity of the forearm is located very close to the point of insertion of orthopedic plates and the weight of the forearm itself is ten times smaller than 15 kg, it may be ignored in the calculations of moment. In this case, the moment M, calculated by eqn. (2) adding the two moments, is 22.2 Nm.
The moment of inertia I for a circular cross-section (70 mm²) can be calculated using the following:
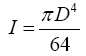 (5)
(5)
and the result is I=390 mm4. Therefore, according to eqn. (1), the theoretical stress is 268 MPa. Figure 1 shows the loading in the region of the ulna and radius.
Performing the same calculations for the dynamic stress, using the maximum possible distance (the most critical), we find a value of 57 MPa.
Thus, as a static criterion for approval, the value of 268 MPa in flexion may be considered for the design of the prostheses used on fracture healing in the regions of both the ulna and radius. And as a dynamic criterion for approval, the value of 57 MPa in flexion may be taken for a product aimed at fracture consolidation in the areas of both radius and ulna.
According to Rikli et al. [18], for forearm in neutral rotation, the force is from 107 N with wrist flexion to 197 N with wrist extension. When the wrist is in radial deviation and the forearm is in supination, the force is 245 N. Consequently, any implant or external fixator used for fracture fixation should have enough resistance to support these loads.
Olecranon
Figure 1 shows the area of application of plates and rods for the olecranon and the tendon insertion region. For olecranon, there are no studies of supported loads. However, it is possible to estimate the loads involved and determine the worst stress this region can face. The rods within the olecranon region do not undergo torsion. The movements of pronation and supination involving rotation are not directly linked to the ulna but to the radius, which undergoes torsional demand, keeping the ulna and olecranon aligned with the whole arm.
After surgery, the doctor asks the patient not to carry weight during the initial process of bone healing. In this condition, only the weight of the forearm itself is to be supported by the region. The weights of the forearm and hand, right and left, are approximately 1.5 kg (15 N). Part of this load is supported by soft tissues, skin, muscles and tendons.
It is observed that in the region of plate for fracture stabilization, there are no insertion points of tendons. In the region of the olecranon, the mechanical loading of the plate is negligible since the tendons hold the daily normal loads. Thus, the plate should support only a fraction of the olecranon.
To calculate the stress that the weight of the arm causes to the olecranon, it is necessary to know the cross sectional area of the most critical region, i.e., the smallest section. There are no conclusive studies about this region. Gomez and Nahum [14] analyzed the geometric properties of the humerus, assuming that the average cross sectional area is 200 mm² for men and 160 mm² for women. For calculation purposes, they considered that the diameter of the most critical region of the olecranon (smallest area) is equivalent to the average diameter of the humerus. They also analyzed the geometric properties of the ulna. They state that the cross sectional average is 90 mm² for men and 70 mm² for women. As to the mechanical properties of the ulna, it is reported that the average stress required to fracture by bending is between 23.0 to 18.7 kg/mm². Applying these values to the olecranon region, which has a larger cross sectional area (160 mm²), the stress can be calculated using eqn. (1). In this equation, the stress given by the moment M multiplied by y (which, in this case, is half the diameter) divided by the moment of inertia of the area, I. The moment of inertia of the cross sectional area of a beam, relative to an axis passing through its center of gravity measures its stiffness, i.e., its resistance to bending in relation to this axis. Therefore, the stress is inversely proportional to the value of the area. By analogy, it is possible to estimate the stress fracture of the most critical olecranon region (160 mm²) as 92 MPa.
Using the same calculations as for the forearm region (radius and ulna) and considering only the olecranon as a support, the stress for a load of 15 kg is 92 MPa.
Performing the same calculations for the dynamic stress (carrying the weight of the arm itself) we obtain a value of 17 MPa.
On the basis of these data, the dynamic approval criterion, the value of 34 MPa (2 × 17 MPa) in flexion, may be taken as a dynamic approval criterion for a product aiming at healing fractures in the olecranon region. The value of 184 MPa (2 x 92 MPa) may be regarded as the static approval criterion for a product with this purpose. Figure 1 shows the data used in the calculations.
Wrist Region
Rikli et al. [18] conducted in vitro and in vivo tests and determined the distribution of forces transmitted through the radioulnocarpal joint under normal physiological conditions. The study showed that the forces are more severe than those reported by other authors. The measured forces in situ tests had values up to 109 N when the limb was subjected to a load of 150 N. In the same study it is mentioned that the soft tissue in the region supports some of the load applied to the joint.
The work of Wolf [19], performed in cadavers, confirms that loads up to 100 N are applied to the tendons of the wrist. Thus, it is advisable to use a force of 100 N as the load criterion for product development aiming applications in the wrist region (Figure 1).
Hand
Biomechanical efforts are applied to the phalanges, metacarpals, the bones of the wrist and the distal radius in daily activities [19,20]. The radiocarpal joint allows all movements except rotation about the longitudinal axis. Movement in the frontal plane includes abduction, sometimes referred to as radial deviation or radial flexion, and adduction, sometimes referred to as ulnar deviation or ulnar flexion. In the sagittal plane, the wrist extends and flexes. Flexion brings the palm to the forearm face. Movement of intercarpal joints is negligible. Carpometacarpal joints are of two types:
a) The thumb joint is a saddle (sellar) joint. This kind of joint allows extensive and peculiar movements;
b) The interphalangeal joints are uniaxial hinge joints and are have only one degree of freedom.
The internal fixation for the proximal phalanx has a moment close to 260 N·cm when a plate fixation occurs without interfragmentary screws. Therefore, the acceptance criterion is that the plates should support a moment of 260 N·cm until the fracture starts, supporting a load of 19 N. This force is larger than the force measured after the flexion of the proximal interphalangeal joint. The consideration is that loading occurs at angles of 60 degrees and 90 degrees, respectively, corresponding to 10 and 14 N in response to what the joint supports [19]. Thus, a value of 260 Ncm can be considered as the most critical since it refers to a product with certain longevity in market.
This criterion, however, may be refined with the use of eqns. (1) and (4). Based on these equations, it is possible to obtain the final stress. The results can be used to evaluate whether the implants will fail.
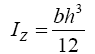 (6)
(6)
In eqn. (4), Iz is the moment of inertia, a property that measures the mass distribution of a body about a rotational axis. The higher the moment of inertia of a body is, the harder it is to make it rotate. Eqn. (4) allows the calculation of the moment of inertia of parts with rectangular section (or similar to rectangular) and depends the base b and the height h.
With eqn. (1) one can determine the stress from the moment based on the y value (half the height h in this case) and Iz. This stress may be used as a definitive criterion.
From the work of Cabibihan et al. [20] it is possible to consider that the phalanx has the shape of body with rectangular section. Considering h=9 mm and b=16 mm, one obtains the values Iz=972 mm4 and M=140 N·mm (for y=4.5 mm) and the stress is 0.65 MPa. This stress can be considered as the acceptance criterion for products in the phalange region.
Based on the literature [21,22], the weights of the forearm and right and left hand are shown in Table 1. The data in Table 1 show that the weight of the hand is approximately 4 N. Assuming that the hand will be entirely sustained by the carpal bones, one can calculate the torque to which the hand will be subjected by its own weight. The length of the extended hand corresponds to 10.8% of the height of the person. The center of gravity of the hand is located at 50.6% from the proximal region. For a person 1.80 m high, the center of gravity of the hand is located approximately 100 mm from the proximal region. Assuming that the entire hand is supported on the proximal region of the metacarpals and with no assistance or support from other bones or soft parts, the situation that generates the largest lever arm is the most critical condition and induces the largest torque, as shown in Figure 1.
Table 1. Hand and arm weights. Adapted from Aerospace Medical Research Laboratory [21].
| Human body part/ weight (kg) | Chandler et al. [21] | Clauster et al. [22] |
|---|---|---|
| Left hand | 0.3737 | 0.374 |
| Right hand | 0.4004 | 0.3932 |
| Left forearm | 1.0888 | 0.7701 |
| Left upper arm | 1.8882 | 1.4845 |
| Right hand | 0.4004 | 0.3932 |
| Right forearm | 1.1132 | 0.821 |
| Right upper arm | 1.8425 | 1.5256 |
| Left thigh | 6.7751 | 5.827 |
| Right thigh | 6.5233 | 5.947 |
| Left calf | 2.6719 | 2252.5 |
| Right calf | 2.6857 | 2.2426 |
| Left foot | 0.8372 | 0.9882 |
| Right foot | 0.8357 | 0.9522 |
Based on these considerations, the moment will be equal to 40 N·cm. According to this calculation, it is possible to consider that a moment of 40 N·cm is the most critical and established as the acceptance criteria for products used in the metacarpal region. This criterion can be refined with the use of eqn. (3).
From the work of Cabibihan et al. [20] one can estimate the width of metacarpal bones of men and women. The average value is 8.3 mm (9 mm for men and 7.6 mm for women). Assuming that the metacarpal has a circular shape, we obtain Iz=232.84 mm4, M=40 N·cm and y=4.15 mm. Based on appropriate substitutions, the stress was found to be 7.13 MPa. This value can be used as acceptance criterion for medical device for metacarpal region.
Tendons
Tendons differ in shape and orientation, depending on their union to muscle fibers. Suture anchors are common implants to be used to attach tendons and other soft tissues. Anchors have been successfully used to repair ligaments and muscle lesions. In relation to the flexor digitorum profundus (FDP) of the hand, Brustein et al. [23] determined that the maximum load applied in the distal interphalangeal joint is 19 N during movement produced by the FDP of the hand.
For the shoulder area, Cole et al. [24] determined that supraspinatus and infraspinatus tendons support maximum tensile forces of 35 N and 665 N, respectively. On the shoulder area, forces of 231 N on average are sufficient to injure the capsule ligamentous complex. The glenoid lesions are known as Bankart lesions.
The mechanical properties for anterolateral ligament (ALL) and inferior glenohumeral ligament (IGHL) are higher than knee capsular tissue. The elastic modulus of ALL is 174 ± 92 MPa and is 139 + 60 MPa for IGHL, which are higher than 62 ± 30 MPa for the capsule. ALL (46,4 ± 20.1 MPa) has higher ultimate stress than capsule (13.4 ± 7.7 MPa) and IGHL (38.7 ± 16.3 MPa) [25].
Lower Limbs
The lower limb has four parts: girdle (pelvis and hip complex), thigh (femur bone), leg (tibia and fibula bone), and foot (with its innumerous bone complex).
Pelvis and Hip Complex
The pelvic girdle is composed by ilium, ischium and pubis bones, which are fibrous interconnected inside the acetabular cavity [26]. The pelvic is responsible to connect the trunk with the lower limbs, which all actuated in synergism during lower extremity movements [27] holding the balance, posture and equilibrium during interactions of ligaments, tendons and muscles from hip complex [28].
The hip region is a proximal joint of the lower limb. Its movements are performed by a single joint, called coxofemoral joint, that has three axes: the transversal axis (in the plane where the movements of flexion and extension are performed), the vertical axis (longitudinal axis that allows the movements of external and internal rotation) and the anterior posterior axis (located in the sagittal plane, which executes the movements of abduction and adduction). The angle between the axis of the femoral neck and the normal femoral shaft is approximately 125 degrees. The coxofemoral joint is formed by the head of the femur, which rotates within the acetabulum, formed by the pelvic bones.
Kirkwood et al. [29] measured the moment, power, range of motion and mechanical work produced by hip and knee joints during gait of a group of 30 men between 55 and 75 years-old. The study includes data on the three planes of motion. The plane that was most critical for calculation of momentum was the sagittal plane. The extensor internal momentum to balance the external flexor forces reached 0.76 N·m/kg at 6% of the gait cycle. The internal flexor momentum at 51% of the gait cycle was 0.64 N·m/kg. Therefore, assuming a person who weighs 80 kg, the most critical momentum that this person will meet in a gait cycle is approximately 61 N·m.
Implants for the hip joint are complex and have several geometries. ISO 7206-9 (Implants for surgery: Partial and total hip joint prostheses: Part 6: Endurance properties testing and performance requirements of neck region stemmed femoral components) [30] norm standardized reference values for fatigue testing. This technical standard suggests an assembly for mechanical test and minimum load (500 N) for fatigue test. The fatigue resistance is 5000 N for 107 cycles.
In a normally standing person, approximately 35% of the body weight is support by the femoral head. The technical standard establishes reference values based on clinical studies. Adequate values are 1200 N for implants whose distance from the center of the head of femur to the farthest point of the implant is less than 120 mm. For intermediate distances, the value is 2300 N. These data are based on values from ISO 7206-630. Figure 2 illustrates the stress in the hip region.
Robinson et al. [31] studied the mechanical properties of hip piriformis tendons to assess different fixation methods and found that the force needed to rupture the hip piriformis tendon was about 300 N.
The head of femur bone fits to pelvis by its insertion as a socket inside the acetabular cavity [26]. The head has a spherical shape and mainly of the bone has cancellous trabecular with a thin cortical belt in order to enhance its structural strength. The amount of spongy bone is responsible for most of the forces distribution upon the hip joint during physiological loading of the structure [26]. Femoral head holds a specific angle of 145° to promote an adequate angle and maintain functional articulation with the hip joint and keep the femur bone away from the body. Besides the strength provide by the ligament, there is also a loose capsule with attachments with the tendons, ligaments, keeping contact with the entire femoral head and most of its head [26].
Literature shows that under fall the femoral neck and the radius are the most vulnerable sites to fracture. Gauthier et al. [32] compared some human (50 - 98 years old) bone anatomical sites (radius and the femoral neck) and analyzed the fracture behavior. Mechanical tests were performed on paired femoral neck, femoral, tibial and radius diaphyseal samples. Their results showed that despite of the anatomical site, the bone has the same fracture properties subject to the fall loading conditions.
Tibia and Femur
For anatomical reduction of olecranon fractures Tejwani et al. [33] compared the biomechanical stability using two methodologies: plates and band wiring. They concluded that posterior plating fixation achieves greater rigid stability than tension band wiring. The plating technique allows compression at the fracture site and reduces the possibility of problems related to postoperative complications.
Musculoskeletal injuries are a serious problem for recruits participating in military training but may be especially important for women. The most common sites of stress fractures in both military and civilian populations are the tibia (25%), metatarsals (21.7%), pelvis (21.7%), and femur (20%). Nonrunners or women who reported running less than 1.5 miles per run were more likely to incur a stress fracture than women who ran 3 or more miles per run [34].
Laurence et al. [35] argue that the stress on bending applied to a bone is limited by the resistance of the ligaments and muscle structures, which are responsible for the force transmission. They measured the torsion strength of a leg bone (tibia) from cadavers and the highest value was 217 N·m for an intact bone. This value reduces to 144 N·m when the tibia is drilled for the insertion of screws. They also tested the strength of the ligaments from cadavers and observed that the highest bending moment of ligaments in the tibia was 170 N·m. However, in normal daily activities, the stress in flexion is limited by the pain threshold of each individual that leads to a maximum moment of 126 Nm. Therefore, there is a natural limitation of the moment that can be applied, which is lower than the strength of the drilled bone. The authors mention the value of 80 N·m as the bending moment supported in daily activities, which is below the threshold of pain.
According to Bergmann et al. [36], who analyzed the loads supported by instrumented implants, a person can transfer about 238% of its body weight to the leg during the common activities in daily life, i.e. for a person with 80 kg, the load transferred to the implant is about 270 kg (2650 N). They also studied the torque to which the femur is subjected during daily activities and found that when an individual is climbing stairs, the femur is subjected to a loading equal to 2.96% (3170 N) of the body weight.
Krischak et al. [37] determined the biomechanical strength in bending and fatigue in side plate fixation devices in the femur of human cadavers. The authors compared sliding hip screw (SHS) with the percutaneous compression plate (PCP). Eight pairs of human cadaver femurs were tested for comparison of the primary stability of the two implants under two tests: cyclic loading up to 200 N, 400 N, 600 N, 800 N, and 1000 N and loading up to failure. They observed that specimens fixed with the PCP showed higher displacements during loading than specimens fixed with SHS. A similar tendency was observed for larger loads. The authors observed that osteoporotic femurs (bone mineral density 184.9 mg/cm) fail when the load exceeds 200 N.
Boswell et al. [38] showed that Locking Compression Plates (LCP) compared to standard nonlocking plates used to stabilize radius fractures showed approximately 95% higher resistance to fracture. LCP resisted 1755 N loads, while standard nonlocking plates supported only 919 N loads.
Regarding the technique used for stable fixation of fractures, Jiang [39] showed that, mechanically, some techniques require more than one kind of fixation. The load of 200 N can be taken as the approval criterion for products in the femoral region and the value of 142 N may be taken as the approval criterion for products in the tibia, fibula and calcaneus areas.
According to Gomez and Nahum [14], who analyzed the biomechanics of human bones, the average cross sectional area of several long bones, including the tibia, is 240 mm² for an adult male and 180 mm² for an adult female. For the femur cross section, the values are of 330 mm² for men and 260 mm² for women. For the fibula, the cross section is 70 mm² for men and 50 mm² for women. These data are valid for persons from 20 to 89 years of age.
The average length of the thigh corresponds to 0.245H, where H is the patient height. The average length of the region below the knee to the foot is equal to 0.246H. For a subject with a height of 1.80 m, the lengths of the femur, tibia and fibula correspond to approximately 440 mm. These data is able to feed eqn. (1) to enable calculations about the stress to which these bones are submitted.
The moment of inertia I for a circular section is given by eqn. (3), and the moment M is given by eqn. (2).
The distance to the point of application d is taken to be the center of each limb in order to obtain the most critical result.
Taking y as half the diameter of the bone, the calculated value for the stress is 91.7 MPa. This stress is used a dynamic criterion of approval for products used in the region of the tibia and 73.3 MPa as a dynamic criterion of approval for products used in the region of the femur.
For the fibula, performing the same calculations, the result is 624 MPa. One should remember that most of the load is supported by the tibia.
Brustein et al. [23] examined the yield stress (minimum stress for plastic deformation) of the femur and tibia in tensile and compressive loading. They found that the yield stress is a function of the age between 20 and 89 years. For the tibia, the yield stress in tensile testing varies from 120 to 140 MPa and the yield stress in compression varies from 183 to 213 MPa. For the femur, the yield stress in tension varies from 104 to 120 MPa and the yield stress in compression varies from 180 to 209 MPa.
Yamada [40] reports that a compression loading of 590 kg induces fracture of the fibula. Considering the cross section previously mentioned, the tension fracture is equal to 116 MPa. These data suggest that the main stress in the tibia is compression, since the tibia supports most of the body weight. Based on these values, one can establish the following criteria:
A stress of 213 MPa is the critical value for the approval of static loading in the case of products used in the region of the tibia.
A stress of 209 MPa is the critical value for the approval of static loading in the case of products used in the region of the femur.
A stress of 116 MPa is the critical value for approval of static loading in the case of products used in the region of the fibula. Figure 2 illustrates the femur and tibia loading.
Knee
Knee is one of the most stables joint in body, allowing adequate forces distribution from foot at the same time as allows a satisfactory interaction of movements between femur and tibia. There is a restraint from the associated ligaments, which participates in accordance with muscles activity in order to assure a correct functional stability of the knee. Most of the mechanical demand that impact knee as load is also amended by the participation of capsule, which has maintained direct relation with muscles and ligaments in neighborhood [41]. The three main articulations that compose the knee joint are known as tibiofemoral, tibiofibular and patellofemoral.
The anterior and posterior cruciate ligaments of the knee are the most complex region of the human body. Kokron et al. [42] determined that the pull resistance is 971 N for the anterior cruciate ligament (ACL) and 993 N for the posterior cruciate ligament (PCL).
The medial patello-femoral ligament (MPFL) seems to be the most important passive patellar stabilizer and it acts 50-60% of the force of the medial soft-tissue which restrains the lateralization of the patella. Criscenti et al. [43] evaluated the tensile behavior of the individual medial patello-femoral ligament (MPFL) of human fresh frozen cadaveric knees and compared with structural ones. They observed that the ultimate stress of the isolated ligament was 16+11 MPa, the ultimate strain was 24.3+6.8%, the Young's Modulus was 116+95 MPa and the strain energy density was 2.97+1.69 MPa. For the whole structure the ultimate load increased to 145+68 N, ultimate strain was 9.5+2.9 mm and the absorbed energy was 818.8+440.7 N mm.
Tibiofemural joint connects two of the biggest bones in body and is constructed by two large condyles (femur side), two separate fibrocartilage menisci between both bones in interaction with two main ligaments (transverse and posterior cruciate), which control anteroposterior and rotational motions of the joint. Laterally, medial and lateral collateral ligaments stabilize the capsule during extended positions.
Tibiofibular joint is a small articulation between the head of the fibula and the posterolateral and inferior site of the tibial condyle. This joint although smaller than the others is responsible to dissipate torsional stresses emerged from foot, relief tibia during bending in lateral orientation and withstand tensile efforts when in consonance with the middle part of the fibula [44].
The patellofemoral joint participates in the connection of the patella with femur, while the posterior region of the patella is articulated to the tibia by the patellar tendon. Another attachment area of patella involves its connection to femur by the patellofemoral and patellotibial ligaments [45].
Foot
Figure 3 shows the bone structures of the human foot. Biomechanical stresses are important for the characterization of primary movements that constitute the walking cycle of an individual. There are two critical points in the structure of the human foot. The first is the Lisfranc joint, which will be referenced to as the tarsometatarsal joint. The second is the relationship between metatarsal and proximal phalanges, referenced to as the metatarsophalangeal joint. The Lisfranc injury (also known as the Lisfranc fracture, Lisfranc dislocation, Lisfranc fracture dislocation, tarsometatarsal injury, or simply midfoot injury) is an injury of the foot in which one, or all, metatarsal bones are separated from the tarsus.
Masson et al. [46] studied the forces on the lower limbs of human cadavers. The authors measured the compressive stress on the calcaneus and on the head of the first and fifth metatarsal bones. They observed that the foot and the calcaneus receive about 60% of a load of 4000 N applied to the foot. Soft tissue disruption occurred under a load of more than 1600 N.
Gait cycle is the period of time between steps and has two parts: stance and swing. In the first part, there is contact between the leg and the supporting surface; in the second, the leg is moving forward with no contact with the surface. Considering that maximum load in compression in daily activities is about 1000 N, and assuming that the load on the calcaneus varies linearly with the applied load, it is possible to show that a maximum force of 400 N is applied directly to calcaneus; this is the expected peak load. However, as Masson et al. [46] in normal daily activities, the maximum value is 142 N.
The lateral ankle ligaments are at a high-risk of injuries during sport activities. About 85–90% of foot and ankle injuries are due syndesmosis and lateral ligament sprains, which is the weakest part of the human lower extremity. The anterior talofibular (ATFF) ligament is the most commonly injured ligament in lateral ankle sprains and calcaneofibular (CFL) ligament is the second. Takao et al. [47] analyzed the ankle ligaments. According to these researchers, the human anterior talofibular (ATFL), posterior talofibular (PTFL) and calcaneofibular (CFL) ligaments are responsible for the stability of the ankle and have resistances to rupture of 139 N, 261 N and 714 N, respectively. Nien et al. [48] determined the in situ mechanical behavior of ankle ligaments at physiological levels of loading. Under elongation of 1.0 mm in the loading region, the posterior calcaneofibular and talofibular ligaments on the lateral side are submitted to a tension force approximately equal to 118 N and 177 N, respectively.
Oldenburg et al. [49] determined the biomechanical strength of ankle prostheses for arthrodesis and found that the vertical forces on the foot during a walk can reach 1000 N or 125% of the body weight.
Rodgers [50] studied the biomechanics of the foot and ankle complex in walking and running and developed the infograph that displays the pressure distribution patterns in four different phases of the gait cycle. The pressure centers are of particular importance, since the foot is composed of three arches (longitudinal, medial and transversal). It is important to note that the pressure is higher in the heel. For the calcaneus region and ahead of the midfoot, the force is about 1.1 to 1.3 times the body weight [50-52]. Visual data provided by Stokes et al. [51], facilitate the understanding. Stress data reported by Rodgers [50], Stokes et al. [51] and other authors are summarized in Table 2.
Table 2. Mean, standard deviation (SD) and maximum stress (Max) on the foot during walking. Adapted from Rodgers et al. [45] and Stokes et al. [46].
| Region | Mean (MPa) | SD (MPa) | Max (MPa) |
|---|---|---|---|
| First metatarsal | 0.32 | ±0.134 | 0.454 |
| Hallux | 0.307 | ±0.127 | 0.435 |
| Lateral midfoot | 0.116 | ±0.030 | 0.146 |
| Lateral heel | 0.349 | ±0.090 | 0.439 |
| Medial fingers | 0.286 | ±0.100 | 0.386 |
| Medial heel | 0.434 | ±0.212 | 0.646 |
| Medial midfoot | 0.057 | ±0.013 | 0.07 |
| Side fingers | 0.174 | ±0.022 | 0.197 |
| Second metatarsal | 0.354 | ±0.109 | 0.463 |
| Side metatarsal | 0.324 | ±0.144 | 0.468 |
Rudd et al. [52] analyzed the absorbed energy by materials used to minimize the risk of fracture in car accidents. The tension absorbed by the material of the car pedals and which would be transferred to the foot during braking range from 0.172 to 0.931 MPa. The values found by Rudd et al. [52] and by Rodgers [50] are similar. The mechanical properties of the materials are important to minimize the transfer of energy to the foot. If there was no absorption of part of the energy by the pedals, the feet could fracture after an impact. One expects that the maximum energy transferred in an impact is lower than the maximum stress that occurs in the calcaneus while walking or running. All values mentioned above are in the same range (from 0.10 kPa to 1.0 MPa). Thus, the value of 1.0 MPa may be taken as the approval criterion for devices used in the forefoot region, the value of 0.15 MPa can be taken as the approval criterion for devices used in the midfoot region and the value of 0.65 MPa can be taken as the approval criterion for devices used in the calcaneus region (Figure 3).
Cervical Spine
The loads applied to the cervical portion of the vertebral column were used as a basis for the acceptance criteria of implants. Figures 4 and 5 illustrates the loading of the implant area.
Moroney et al. [53] examined the loads in the structure of the neck during physical tasks. The mean neck load in male subjects was 29.7 N·m. In female the mean load was 10% to 40% smaller. They observed that the contraction force of the neck muscles was 180 N. The most critical loading was the compression force on the C4-C5 vertebral segment (1164 N); the lateral shear forces was 125 N and anteroposterior shear force was135 N. Intervertebral implants as subjected to a static compressive strength of 4929 N and a dynamic compression strength of 534 N for 5 million cycles.
Ivancic et al. [54] investigated the tensile mechanical properties of human cervical spine, studying the anterior longitudinal ligament, the supraspinous ligaments, middle-third disc ligament, capsular ligament and ligamentum flavum. He elongated to complete rupture 97 bone-ligament specimens (C2-C3 to C7-T1) prepared from six cervical spines (average age, 80.6 years; range, 71 to 92 years). The results showed that the highest average peak forces, 244.4 and 220.0 N, occur in the ligamentum flavum and the capsular ligament, respectively. These loads were significantly greater than in the anterior longitudinal ligament the supraspinous ligament and the middle-third disc. These results show that if the region is subjected to a force higher than 244 N, the ligaments will break, as well as less resistant structures, such as the spinal cord.
Considering a head weight of 50 N, the dynamic compressive force applied in the cervical region is 150 N (Allen et al. [55]). Other researchers [56] reported that the average weight of the human head of a big adult is about 5.3 kg and about 20% of this value is supported by the ligaments. Thus, only 80% of this value (42 N) would be supported by the vertebrae or by implants applied to this region.
Based on these data, it is reasonable to assume a force of 150 N for static loading and 42 N for dynamic loading are reasonable criteria for daily activities. The majority of patients who require this kind of implant have unstable cervical or are tetraplegic, i.e., they will be at complete rest during treatment, when the fused part will act in occipital-cervical support.
Yogandan et al. [57], in a study of automotive collisions, found that the forces reach values of the order of 500 N and moments of the order of 4 N·m. These loads cause failure of the occipitocervical junction, with degeneration of the cervical intervertebral discs. This value of 4.0 N·m (at an angle of 30°) may be set as the acceptance criterion for torsion. The technical Standard ASTM F2423 (Standard guide for functional, kinematic, and wear assessment of total disc prostheses) [58] recommends a torque of 4.0 N·m as the torque for testing of cervical IVD (intervertebral disc) prostheses. Standard F2423 recommends 12 N·cm for test profiles for lumbar IVD prostheses. According to the literature [57], the torsion values used in cervical biomechanical analysis are in the 1.5 to 2.5 N·m range. Panjabi et al. [56] indicate that the maximum load rotation for the cervical disc is 1.8 N·m. The criteria for approval of the devices are summarized in Table 3.
Table 3. Test profiles for spine prostheses.
| Mechanical test | Approval criterion |
|---|---|
| Static compression | 130 MPa |
| Dynamic compression | 42 MPa |
| Static shear | 135 MPa |
| Dynamic shear | 135 MPa |
| Static torsion | 12.0 N |
| Dynamic torsion | 1.8 N |
| Subsidance | 857 N |
| Subsidance | 242 N |
Compression Loading of Thoracic‑Lumbar Spine
Figure 5 shows the loading application in the thoracic-lumbar region. The load conditions in the spine are highly complex and measurement is extremely uncertain. It is not possible to measure accurately the loading in a particular vertebra during normal daily activities, since the biomechanics of the spine of each individual adapts to posture during loading. Two individuals performing the same movement may feel the loading differently.
Claeson and Barocas [59] analyzed biaxial loading on human cadaveric lumbar facet capsular ligament (FCL) tissue. They observed that at maximum extension the shear forces (mean values of 1.68 N and 3.01 N in the two directions) is comparable to the normal forces perpendicular to the aligned collagen fiber bundles (4.67 N) and smaller than normal forces in the fiber direction (16.11 N).
Schultz et al. [60] tried to predict the loads on the spine and muscle contraction forces and compared predictions with measurements of intradiscal pressure and myoelectric activity. They found values between 0.27 MPa for relaxed standing position. The most critical pressure is 1.62 MPa for standing position, hips flexed at 30 degrees, arms outstretched in front with 4 kg each.
Nightingale et al. [61] explored the inertial effects of the head mass and torso on cervical spine dynamics constraining. In their experiments data for the head impact forces and the reactions at T1 were recorded. Under impact velocities on the order of 3.2 m/s (11.5 km/h) the average compressive load was 1727 + 387 N. Decoupling was observed between the head and T1.
Wilke et al. [62] measured an intradiscal pressure. They implanted a pressure transducer in the nucleus pulposus of a nondegenerated L4–L5 disc of male volunteer 45-years old and weighing 70 kg. The pressure was recorded during 24 hours for various activities: sitting in a chair, in an armchair and in a pezziball (ergonomic sitting ball); during sneezing, laughing, walking, jogging, stair climbing, load lifting; and others. The measured pressures were: lying prone, 0.1 MPa; lying laterally, 0.12 MPa; relaxed standing, 0.5 MPa; standing flexed forward, 1.1 MPa; sitting unsupported, 0.46 MPa; sitting with maximum flexion, 0.83 MPa; nonchalant sitting, 0.3 MPa; lifting a 20-kg weight with round flexed back, 2.3 MPa; lifting a 20-kg weight with flexed knees, 1.7 MPa; and lifting a 20-kg weight close to the body, 1.1 MPa. During the night, the pressure increased from 0.1 to 0.24 MPa. According to Wilke et al. [62], the stress supported by the spine of a walking person reaches 0.65 MPa. Considering the area of the vertebra which will support the load as 1200 mm2, a 780 N supported load is reached, while in standing position lifting a 20 kg weight with round flexed back, the stress reaches 2.3 MPa for 2700 N. They concluded that the intradiscal loading is influenced by the lordotic curvature of the spine, by the type of activity undertaken and by muscle interference.
Rohlmann et al. [63] and Scott [64] measured the loads on internal fixation of the spine during walking on a flat surface and climbing stairs. The authors determined the influence of the velocity and the manner of walking. They found values of the axial compressive load of up to 125 N for the left side and about 150 N for the right side in most critical activities. In other study, Rohlmann et al. [65] performed measurements of applied moments on the spine. They measured the maximum moments separately. The values were 2.8 N·m on the left side and about 0.3 N·m on the right side, totaling 3.1 Nm. The load on the lumbar spine may be 1.2 times larger than the body weight of the subject during gait.
According to Rohlmann et al. [63] climbing or descending stairs, which is part of the normal daily activities, the spine is subjected to a compression load of about 300 to 400 N. They measured real loads using extensometers.
According to Schultz et al. [66], the reaction forces and not the external forces induce the increase of compressive loads on the spine. It may be that the movement of bending down to pick up a sheet of paper induces greater forces in the hips than lifting a heavy weight. These loadings were determined by myoelectric activity and the measurement of intradiscal pressures.
According to Heller et al. [67], the spinal ligaments suffer ruptures with loads of 692 N. The rupture load range determined in assays is in the range from 220 to 1590 N.
Table 4 presents the results compiled from the literature (prioritizing in vivo testing) considering only one decimal digit.
Table 4. Theoretical loading and stress applied to the spine.
| Reference | Loading | Note |
|---|---|---|
| Wilke et al. [62] | 0.1 MPa<S<2.3 MPa | In vivo testing during daily activities with supposed surface of disc L4-L5 1800 mm2. |
| Schultz et al. [60] | 0,3 MPa<S<1.6 MPa | In vivo testing for different postures |
| Wilke et al. [62] | F=2510 N | Calculus based on Wilke et al. [62], who suggested F=445 N |
| Rohlman et al. [65] | F<150 N M<3.1 N×m |
Climbing or descending stairs |
| F<150 N M<6.4 N×m |
For in vivo and in vitro testing | |
| F=1.2 W | Walking |
S: stress; F: compressive force; W: body weight; M: moment.
Loads on an internal spinal fixation device during walking.
Comparison of loads on internal spinal fixation devices in vitro and in vivo.
The area of a vertebra was considered to be 1800 mm2. The sectional area of the device was considered to be equal to 62 mm2 for the purpose of determining compressive stress [67]. They assumed the weight of an obese person (200 kg), i.e., a very critical situation. For this situation, we have to calculate the stress through the compression load and taking into account the bending moment. Table 5 shows the calculated stress.
Table 5. Theoretical stress applied to the spine.
| Author | Results | Comments |
|---|---|---|
| Wilke et al. [62] | T<2.3 MPa | In vivo testing during daily activities with supposed surface of disc L4-L5 1800 mm2. |
| Schultz et al. [60] | T<1.6 MPa | In vivo testing for different position |
| Wilke et al. [62] | T=1.4 MPa | Based on Wilke et al. [62], who suggested F=445 N |
| Rohlman et al. [65] | T(F)<2.4 Mpa T(M)<124.2 MPa*** |
Climbing or descending stairs |
| T(F)<2.4 Mpa T(M)<256.3 MPa*** |
For in vivo and in vitro testing | |
| T=1.3 MPa | Walking |
S: tensile stress; CS: compressive stress; SM: stress induced by the moment
Loads on an internal spinal fixation device during walking.
Comparison of loads on internal spinal fixation devices in vitro and in vivo.
***Results considering the moment M in eqn. (2), Iz in eqns. (4) and (3).
The technical standard ASTM F1717 (Standard test methods for spinal implant construct in a vertebrectomy model) [68] covers the materials and methods for the static and fatigue testing of spinal implant assemblies in a vertebrectomy model. The standard is clear and mentions that the test methods are not intended to define levels of performance, since sufficient knowledge is not available to predict the consequences of the use of a particular device. The test results of a product cannot be used directly to predict the in vivo performance. The results can be used to compare different component designs in terms of the relative mechanical parameters. According this standard, the moment can be calculated in the bar tests. The lever arm between the load and the fulcrum is 40 mm. The moment is given by eqn. (2). Performing the calculation, we find a value of 62.6 mm for y=3.125 mm. Thus, determining the moments and moments of inertia, and having the value of y, it is possible to calculate the stress from the moments, as planned. Table 4 shows the results. One can see that there is a small dispersion of the results based on the stresses and a high dispersion of the results based on the bending moment. The difference is not due to a lack of precision, but to the different nature of each measurement.
For static compression testing, a good acceptance criterion is 256.3 MPa. This is the highest value in Table 5 for actual situations and is confirmed by Rohlmann et al. [65].
In dynamic bending tests, one can use one criterion for the axial component testing and another for flexion-compression testing. According to the data in Table 5, the most critical criterion is that suggested by Rohlmann et al. [65] where there is an axial component of 2.4 MPa and a flexion-compression component of 256.3 MPa. Thus, these values are taken as criterion for acceptance of stress.
For static torsion testing, we adopted as a reference the study by Jirková et al. [69]. These researchers performed experimental measurements of the lumbar spine stiffness, considering the torsional stiffness of the segments relevant to the product. The torsional stiffness may be defined as the ratio between a given moment (in this case the torsion around the axial direction of the lumbar spine) and the deformation of the spine for this moment. The maximum torsional stiffness found was 160 N·cm/degree. This will be the acceptance criteria adopted, since the torsion stiffness is the analogue of Young modulus to a common tensile testing. When the material strength is higher than 160 N·cm/degree, it is reasonable to assume that its resistance to deformation in torsion is adequate while performing the movement. Thus, the reference value of 160 N·cm/degree may be set as the acceptance criterion for these products in torsion.
Pull Loading of Thoracic‑Lumbar Spine
Rohlmann et al. [70] performed a study to complement the information gathered by Wilke et al. [62], who analyzed the compression of the spinal discs. The authors collected data during physical activities such as jogging, jumping, and parallel bars exercise. They used two techniques: intradiscal and internal fixation. In the intradiscal technique a transducer captures the pressures inside the spinal disc. The internal transducers were fixed bilaterally inside the posterior region of the vertebral column and measured the stress applied in the spine.
Figure 4 shows the outline of pull load on the vertebral column.
From the data collected from volunteers, it was observed that when they suspended their bodies on the arms (parallel bars) keeping the legs in a sitting position, the compressive stresses were reduced by approximately 30% relative to the stress in the standing position. According to Wilke et al. [62] even removing the pressure exerted by the body on the spine, the loads on the disc and on the functional unit are not fully eliminated due to the muscular action, which tends to contract to support the lower limbs. Thus, it is possible to conclude that the spine is constantly under compression, even when all the weight on the legs is relieved, i.e., spinal traction or spinal disc decompression do not occur naturally. This result was confirmed by Weidle [71], which found that in the treatment of spinal disc decompression for pain relief, the spine is constantly subjected to compressive forces. Tensile stress on the spine is not natural.
According to Nordin and Frankel [72], in the relaxed standing position, the internal pressures on the third and fourth lumbar disc are about twice the weight of the part of the body above these discs. This high pressure is produced by bending the torso to front, which increases the inclination moment of the anterior spine, ventrally compressing the annulus fibrosus of the spinal disc. In the same movement, the posterior region of vertebral spine relaxes, causing the dorsal region of the annulus fibrosus to be tensioned. In this case, there is no tensile force on the spine, but there is tensile on the posterior portion of functional spine unit due to the bending moment. The posterior longitudinal ligament is attached to the vertebral discs and to the posterior border of bodies of the vertebrae extending from C2 to the sacrum, being wider at the thoracic and lumbar regions. This ligament has a great importance in maintaining the integrity of the vertebral column, avoiding its subsequent hyperflexion and posterior protrusion of the nucleus pulposus of the disc.
Any device attached to the posterior region of the spine suffers the action of tensile loads resulting from a bending moment and the resistance offered by the posterior ligament.
The minimum stress that the device should support is equivalent to the load of 324 N that causes the rupture of this ligament. This value can be adopted as a criterion for acceptance for flexion-traction testing for implants.
Thoracic Region - Chest
Figure 5 shows the loading of the ribs. During breathing, the normal force equal to 35 N is applied to the sternum [73]. According to Casha et al. [74] a person with a weak cough can apply to the sternum a force of about 560 N. However, the surgical technique recommends that at least three plates be used for closure of the sternum, so that the loads are divided by three blockage systems. In the case of closure with sutures, it is recommended to use at least six wires so that the forces exerted during daily activities will not tear the sternum bone [75].
For purposes of project approval criteria, the fatigue strength of the device must be larger than 560 N [74]. The value of 600 N is an appropriate value for the peak force to which the product should resist.
This review provides an overview of the biomechanic relations established among different human bones during execution of routinely daily activities. Physiological bone loading in the human body demanded for the development of products used in fracture fixation. This manuscript described the forces stress values and moments acting on different regions of human body.
At glenohumeral region, the load transmitted to a hypothetical device demanded is at least 1260 Kgf. Efforts at humerus revealed this bone can stand forces until 2840 N and 1510 N under compression-torsion and bending efforts, respectively. Any medical device developed should consider a stress value of 450 MPa and moment of 0.43 Nm/degree when aiming on the fracture consolidation in this area. Stress at olecranon region is around 184 MPa during static condition, while at forearm loads vary from flexion to extension and the highest load to be stand by a medical device is 245 N when radius and ulna bones are in supination. Wrist region bears to loads about 100 N during daily activities and hands stand a stress of 7.13 MPa at each metacarpal. At Hip complex, 35% of body weight is stand by femoral head being a prosthesis neck requested to support a fatigue life of at least 107 cycles. A stress value of 213 MPa and 116 MPa were referred to regions of tibia and fibula when submitted to static loadings, respectively. At ankle, any prosthesis is generally leaded with more 125% of body weight during a routinely walk.
The approach presented biomechanical paradigms and interpretation of the human bone loading during normal daily activities that should be useful to students, researchers, engineers and manufacturers of medical devices.
We thank Carlos Chagas Foundation for Research Support from the Rio de Janeiro State (FAPERJ) and the National Council of Technological and Scientific Development from Brazilian Government (CNPq) for supporting this study via grants: E-26/201.759/2015, E-26/201.828/2015, E-26/010.001.262/2015 and 168807/2017-3.