Keywords
|
| Haversine Formula, Dijkestra Algorithm, Google Map, XML |
INTRODUCTION
|
| The drawbacks occurred in previous paper of shortest path detection by using Dijkestra algorithm is recovered in this paper by using A* algorithm. A* algorithm is heuristic in nature. |
| The aim of Paper is to find the route between two places within a city entered by user using the Junctions between Source and Destination junctions. The motto behind it is to improve navigation of user within a city; especially in India where Town Planning policy doesn’t follow a standard rules for naming the different places. Most of the times an unknown person can’t find even the most famous places within the city due to absence of significant identities. Hence the paper is intended to give an appropriate route to user by directing it through various junctions and roads which will be easily identified by the associated landmarks and a Google map. |
| The route is given in two parts as: |
| 1) Text route containing route providing a junction to junction movement to user along with the appropriate directions and turnings guiding the user to get the exact intermediate junctions or landmarks |
| 2) Google Map for exact requested route. |
| Paper uses client-server architecture. Communication between them is strictly in XML for flexibility. The client has user interface from where an input is taken in XML for processing. The server consists of a Java Processing Application and Database for it. The Database used by processing application is a Relational database containing whole information about city. The processing application after parsing request computes route between them with all necessary details with Latitude/Longitude for Google map and sends it as XML response. Client again parsing response gets it on User Interface with Google map processing done in JavaScript. |
PROBLEM DEFINATION
|
| The Aim of Paper is to find out the route in between two spots/junctions within a city entered by user by making use of the Junctions in between the Source and Destination spots/junctions. The main motto behind it is to improve the navigation of user within a city; especially in Indian cities where Town Planning policy doesn’t follow a standard rules for numbering or naming the different spots or places. Most of the times an unknown person can’t find even the most famous places within the city due to absence of naming boards or other significant identities. Hence the project is intended to give an appropriate route to user by directing it through various junctions and roads which will be easily identified by the associated landmarks provided with the route. |
| The requested route is given to user in terms of the junctions present in between the source and destination route along with landmarks and roads connecting them. The Landmarks used in the route may be significant Buildings, Statues, Roads, Complexes, Monuments, Temples, etc. The use of Landmarks adds an advantage of getting to the exact place having no significant identity while travelling through route supplied to user making the application friendly to the user unknown of the city to find out the route in between any two spots or junctions in the city. |
| The application is bound to give the shortest route providing a junction to junction movement to user along with the appropriate directions and turnings guiding the user to get the exact intermediate junctions (with their significant landmarks) or landmarks in particular areas in between two junctions/spots supplied by user. |
LITERATURE SURVEY
|
| This paper contains “great circle distance” which represents the shortest path for distance modeling and optimal facility location on spherical surface. Great circle distances takes into consideration the geometrical reality of the spherical Earth and offers an alternative to widely held notion that travel over water can be exactly modelled by Euclidean distances. The need for geometrical presentation of the spherical earth becomes very relevant when we take into consideration an ever increasing junctions inside a city. The use of “Great circle distances” opens up another avenue for convergence of Navigation and Spherical Trigonometry into advancement of logistics and facility location. In this paper an evaluation of distance location using great circle distances is used to demonstrate the application of the concept[4][3]. |
| This paper proposes and implements a method for performing shortest path calculations taking crowdsourced information, in the form of constraints and obstacles, into account. The method is built on top of Google Maps (GM) and uses its routing service to calculate the shortest distance between two locations. Users provide the constraints and obstacles in the form of polygons which identify impassable areas in the real world[5]. |
A. Haversine Formula
|
| The Haversine formula is an equation important in navigation, giving great-circle distances between two points on a sphere from their longitudes and latitudes [4]. |
| These names follow from the fact that they are customarily written in terms of the haversine function, given by haversin (θ) = sin2 (θ/2). The haversine formula is used to calculate the distance between two points on the Earth’s surface specified in longitude and latitude. |
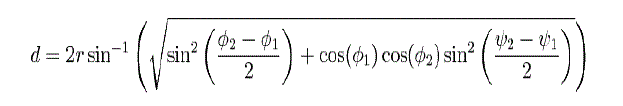 |
| d is the distance between two points with longitude and latitude (ψ,φ) and r is the radius of the Earth. Translation to SQL statement[1] |
| 3956 * 2 * ASIN ( SQRT (POWER(SIN((orig.lat - dest.lat)*pi()/180 / 2), 2) +COS(orig.lat *pi()/180) *COS(dest.lat * pi()/180) *POWER(SIN((orig.lon - dest.lon) * pi()/180 / 2), 2)) ) AS distance [2]. |
B. A* Algorithm
|
| A* uses a best-first search and finds a least-cost path from a given initial node to one goal node (out of one or more possible goals). As A* traverses the graph, it follows a path of the lowest expected total cost or distance, keeping a sorted priority queue of alternate path segments along the way. |
| It uses a knowledge-plus-heuristic cost function of node (usually denoted) to determine the order in which the search visits nodes in the tree. The cost function is a sum of two functions: |
| ? the past path-cost function, which is the known distance from the starting node to the current node |
| ? a future path-cost function, which is an admissible "heuristic estimate" of the distance from to the goal |
Pseudo Code:
|
| function A*(start,goal) |
| closedset := the empty set // The set of nodes already evaluated. |
| openset := {start} // The set of tentative nodes to be evaluated, initially containing the start node |
| came_from := the empty map // The map of navigated nodes. |
| g_score[start] := 0 // Cost from start along best known path. |
| // Estimated total cost from start to goal through y. |
| f_score[start] := g_score[start] + heuristic_cost_estimate(start, goal) while openset is not empty |
| current := the node in openset having the lowest f_score[] value |
| if current = goal |
| return reconstruct_path(came_from, goal) |
| remove current from openset |
| add current to closedset |
| for each neighbour in neighbor_nodes(current) |
| tentative_g_score := g_score[current] + dist_between(current,neighbor) |
| if neighbor in closedset |
| if tentative_g_score >= g_score[neighbor] |
| continue |
| if neighbor not in openset or tentative_g_score < g_score[neighbor] |
| came_from[neighbor] := current |
| g_score[neighbor] := tentative_g_score |
| f_score[neighbor] := g_score[neighbor] + heuristic_cost_estimate(neighbor, goal) |
| if neighbor not in openset |
| add neighbor to openset |
| return failure; |
| function reconstruct_path(came_from, current_node) |
| if current_node in came_from |
| p:=reconstruct_path(came_fromcame_from[current_node]) |
| return (p + current_node) |
| else |
| return current_node. |
| The above pseudo code assumes that the heuristic function is monotonic, which is a frequent case in many practical problems, such as the Shortest Distance Path in road networks. However, if the assumption is not true, nodes in the closed set may be rediscovered and their cost improved. |
SYSTEM DESIGN
|
| The Aim of the paper is to find out the route in between any two spots within a city entered by the user. This can be implemented using a client-server architecture where a request having two junctions as Source and Destination is sent from client to server and requested route is returned to client as a response from server. |
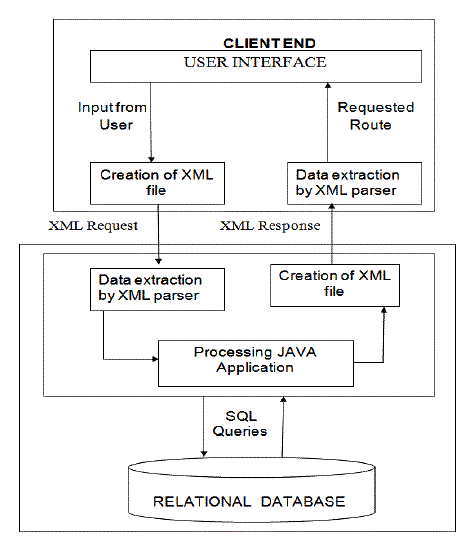
| The client-server implementation assumes that the user accesses the functional application remotely from client end to server one. This makes a clear idea of having client at one machine remotely accessing the application and server at the other. Therefore the design includes significant components shown in functional project design below: |
| The client end consists of user interface from where an input is taken for processing. The server end consists of a Java Processing Application and Database for it. The processing application basically takes only start and end junctions and computes the route in between them with all necessary details having intermediate junctions with landmarks and roads in a particular area. The Database used by processing application is a Relational database containing whole information about city in terms of junctions, landmarks, roads and areas. |
| The input containing source and destination junctions for the requested route is sent to the server end as a request from client end. This request is embedded in a XML file can be called as XML request to be sent to server. At server on receiving a XML request; it is supplied to a XML parser for extracting necessary data i.e. source and destination junctions which are in turn supplied to Java Processing application as an input. This application computes a requested route (a shortest one) by interacting with the database using SQL queries to obtain necessary information for computation. For a computed route to be sent to client, it is again embedded into a XML forming a XML response. This response on receiving at client end is again sent to a parser to extract a route to be displayed to the user at to user interface. |
A. Shortest route in the form of text route and graphical way:
|
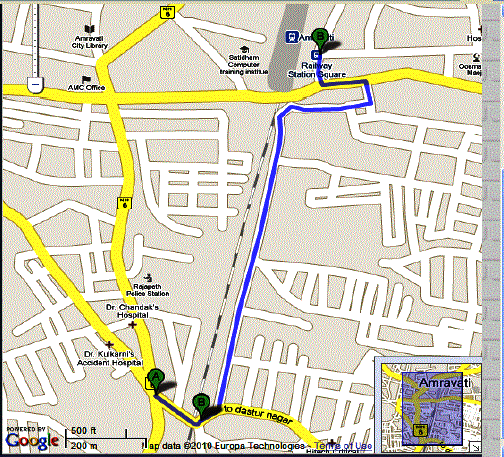
| A user has provision to know the shortest path from source to destination in two ways text based route and graphical route by using Google map. A text based route gives exact way from source to destination in the form of directions, turns, intermediate spots and distance between that spots. A path is given to user by using SQL query. At last it gives the total shortest distance from source to destination. |
| Graphical representation of shortest route is shown in figure. It highlighted the shortest route from source to destination. User can use both the techniques to easily know the route between source to destination. GPI provides different methods to access the highlighted route. |
CONCLUSION
|
| “Landmark Based Routing in Indian Cities” is bound to give the shortest route providing a junction to junction movement to user along with the appropriate directions and turnings guiding the user to get the exact intermediate junctions (with their significant landmarks) or landmarks in particular areas in between two junctions/spots supplied by user. The user also gets exact route with guidance of embedded Google Map. |
FUTURE SCOPE
|
| The drawbacks occurred in previous paper of shortest path detection by using Dijkestra algorithm is recovered in this paper by using A* algorithm. In this paper, we use A* algorithm for determining shortest path between two junctions. But A* is heuristic in nature it means that A* algorithm does not give any guaranty for good solution. Actually this is property of any heuristic algorithm A* algorithm. So, we can use any algorithm associated with A* algorithm which can give best solution to calculate shortest path between two city. A* algorithm is combination of Dijkestra algorithm and Breadth First Search algorithm. In addition to that, A* is heuristic in nature.This System can be applied as a navigation syatem which can navigate through out city. Along with intracity shortest path detection ,we can implement same concept for intercity. |
| |
Figures at a glance
|
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
|
| |
References
|
- By Mr. Reid “Shortest distance between two points on earth” http://wordpress.mrreid.org/haversine-formula/ This is an electronic document. Date of publishing 20/12/2011.
- Samuel Idowu, Nadeem Bari, “A Development Framework for Smart City,” Luleå University of Technology International journal of Computer Application, vol 6, 9 Nov. 2012
- Javin J. Mwemzi, Youfang Huang , ”Optimal Facility location on spherical surfaces”, New york sciences Journal, April 2011.
- Ben Gardiner, Waseem Ahmad, Travis Cooper,”Collision Avoidance Techniques for unmanned Aerial Vehicles”, Auburn University, National Science Foundation, 08/07/2011.
- Simeon Nedkov, Sisi Zlatanova, “Enabling Obstacle Avoidance for Google maps”,June 2011.
- Bing Pan,john C. Crotts and Brian Muller,”Developing Web Based Tourism Information using Google Map” Departemnt of Huminity and Tourism Mangement,Charston ,USA.
- ElinaAgapie.jason Ryder, Jeff Burke, Deborth Estrin, ”Probable Path Interference for GPS traces in cities”, university of California,2009.
- K.M.Chandy,J. Misra, “Distributed Computation on Graphs: Shortest Path Algorithm”, University of Texas, March 1982.
- Siemens AG. Munchen, Ulrich Lauther “An Extremely Fast Exact Algorithm for Finding Shortest Path in static network with geographic backgroung”, International journal on Computer science and Engineering, June2006.
- Philip Klein,Satish Rao ,Monika Rauch, Sairam Subramnyam, “Faster Shortest Path Algorithm for Planner Graphs”, March 1994.
- Andrew v. Goldberg, Haim Kaplan, Renato F. Werneck, “Efficient Point to point shortest Path Algorithm”, Internation Research on Advance Research in Computer Science and Software Engineering, Oct 2005.
|