International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

LBMP: A Logarithm-Barrier-Based Multipath Protocol for Internet Traffic Management

S.Thirunavukkarasu, Dr.K.P.Kaliyamurthie
  1. Assistant Professor, Dept of IT, Bharath University, Chennai-73, India
  2. Professor&Head, Dept of IT, Bharath University, Chennai-73, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Traffic management is the adaptation of source rates and routing to efficiently utilize network resources. Recently, the complicated interactions between different Internet traffic management modules have been elegantly modeled by distributed primal dual utility maximization, which sheds new light for developing effective management protocols. For single-path routing with given routes, the dual is a strictly concave network optimization problem. Unfortunately, the general form of multipath utility optimization is not strictly concave, making its solution quite unstable. Decompositionbased technique like TRaffic-management Using Multipath Protocol (TRUMP) alleviates the instability, but their convergence is not guaranteed, nor is their optimality. They are also inflexible in differentiating the control at different links. In this paper, we address the above issues through a novel logarithm-barrier-based approach. Our approach jointly considers user utility and routing/congestion control. It translates the multipath utility maximization into a sequence of unconstrained optimization problems, with infinite logarithm barriers being deployed at the constraint boundary. We demonstrate that setting up barriers is much simpler than choosing traditional cost functions and, more importantly, it makes optimal solution achievable. We further demonstrate a distributed implementation, together with the design of a practical Logarithm Barrierbased-Multipath Protocol (LBMP). We evaluate the performance of LBMP through both numerical analysis and packet-level simulations. The results show that LBMP achieves high throughput and fast convergence over diverse representative network topologies. Such performance is comparable to TRUMP, and is often better. Moreover, LBMP is flexible in differentiating the control at different links, and its optimality and convergence are theoretically guaranteed.

Keywords
Traffic Management, convergence, Multipath Routing, Utilization

INTRODUCTION
THE Internet has evolved into an ultra large and complex system interconnecting diverse end-hosts and transmission links, with numerous applications running over it. Traffic management thus becomes a critical challenge to the healthy operation of the Internet. To this end, various traffic management tools have been developed, including TCP congestion control at end-hosts, traffic engineering by network operators, and adaptive routing algorithms performed by routers, as shown in Fig. 1. They all target efficient utilization of network resources and quality service to end users. Unfortunately, the collaboration among them is far from being perfect.
The logarithmic barrier method is a powerful optimization method for constrained optimization, in which logarithmic terms are introduced to prevent feasible iterates from moving too close to the boundary of the feasible region [2]. In this paper, we address the above issues through a novel logarithm-barrier-based approach. Our approach jointly considers user utility and routing/congestion control. It translates the multipath utility maximization into a sequence of unconstrained optimization problems, with infinite logarithm barriers being deployed at the constraint boundary. We demonstrate that setting up barriers is much simpler than choosing cost functions and, more importantly, it makes optimal solution achievable. It can be shown that the sequence of the unconstrained optimization approaches to the optimal solution of one of the original problems . We further demonstrate a distributed implementation, together with the design of a practical Logarithm-Barrier-based Multipath Protocol (LBMP). Our LBMP also allows every link to be configured with different control parameters, providing flexibility in dealing with traffic bursts. We evaluate the performance of LBMP through both numerical analysis and packet-level simulations. The results show that LBMP achieves high throughput and fast convergence over diverse representative network topologies. Such performance is comparable to TRUMP and is often better. In addition, LBMP is flexible in differentiating the control at different links and its optimality and convergence are theoretically guaranteed.

MULTIPATH UTILITY MAXIMIZATION
Multipath utility maximization appears naturally in many resource allocation problems in communication networks, such as the multipath flow control, the optimal quality of- service (QoS) routing and the optimal network. It is shown in that even the single-path utility maximization is NP-hard and generally has a duality gap. An equilibrium of TCP/IP exists if and only if the single path utility maximization has no duality gap. In this case, TCP/IP incurs no penalty in not splitting traffic across multiple paths. Such equilibrium gives a solution to the single-path utility maximization and its Lagrangian dual, but can be quite unstable.
We focus on a network of directed links, l belongs to L, and origin destination pairs, s belongs to S. Each origin destination pair represents a source of traffic (or source in short) in the network. Associated with a source is a set of routes, each being a set of links. We represent the routing by matrix Rls that captures the fraction of source s’s flow traversing the links, and we let cl denote the capacity of link l. As shown in the network utilization maximization problem can be formulated as
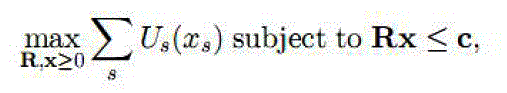image
Where both R and x are variables. The utility functions Us are increasing, strictly concave, and twice continuously differentiable. For single-path routing that is widely used in the current Internet, R is a 0-1 matrix. Set Rls = 1; if link l is in a path of source s; and set Rls = 0 otherwise. It is known that single- path routing limits the achievable throughput. If a flow can be flexibly divided and delivered over multiple paths, higher efficiency and robustness can be expected.
Dual-based Utility Maximizing Protocol (DUMP) is constructed from a distributed solution of using decomposition. DUMP is similar to the TCP dual algorithm in , except that the local maximization is conducted over a vector zs, as opposed to a scalar xs only. DUMP, however, has poor convergence behavior with greedy flows, because the sources can only reduce their sending rates after packet losses. In addition, its utility is based on throughput only. As such, some links will be operating at close-to-full capacity, resulting in long delays, particularly with traffic bursts.

MULTIPATH UTILITY MAXIMIZATION
Our LBMP is derived using a Barrier function technique ,which translates a constrained optimization problem into a sequence of simpler unconstrained optimization problems; it then constructs infinite barriers at the constraint bounds, and ensures every optimization iteration strictly meet the respective constraints. We will demonstrate three noticeable benefits of applying this barrier function method in the multipath traffic management context. First, setting up barriers is much simpler than choosing cost functions; second, with commonly used logarithm barriers, it enables exact solution to the multipath utility maximization; and finally, every link can be allocated with different control parameters, providing flexibility in dealing with traffic bursts.

Multi-path streaming: Optimization of load distribution
Under the current Internet infrastructure, quality of service (QoS) in the delivery of continuous media (CM) is still relatively poor and inconsistent. In this paper we consider providing QoS through the exploitation of multiple paths existing in the network. Previous work has illustrated the advantages of this approach. Here we extend this work by considering a more expressive model for characterizing the network path losses. In particular, we pr oppose a variation on the Gilbert model wherein the loss characteristics of a path depend on an application’s transmission bandwidth. Using this model, we show the benefits of multi-path streaming over best single-path streaming, under optimal load distribution among the multiple paths. We use extensive simulation and measurements from a system prototype to quantify the performance benefits of our techniques.

Optimal traffic splitting
we present a framework for determining appropriate traffic splitting between the multiple paths used for CM streaming. We use the achieved loss rate and lag-1 autocorrelation as our objective functions.

Optimization based on achieved loss rate
We first consider the minimization of the loss rate, PM, achieved at the receiver as our objective. For path j, let Fj (b) denote the functional transition rate from state 0 to 1 when the streaming traffic on path j is b pkts/s. Similarly, Bj (b) denotes the functional transition rate from state 1 to 0 when the streaming traffic on path j is b pkts/s. Let us first consider a simple case wherein there are two paths available for CM streaming. We define Fj(αjλ) = Fj(αjλ)/(Fj(αjλ) + Bj(αjλ)), for j = 1, 2 and express the achieved loss rate as P2 = α1F1(α1λ) + (1 − α1)F2((1 − α1)λ).

CONCLUSION
We consider the problem of congestion-aware multipath routing in the Internet. Currently, Internet routing protocols select only a single path between a source and a destination. However, due to many policy routing decisions, single-path routing may limit the achievable throughput. In this paper, we envision a scenario where multi-path routing is enabled in the Internet to take advantage of path diversity. Using minimal congestion feedback signals from the routers, we present a class of algorithms that can be implemented at the sources to stably and optimally split the flow between each source-destination pair. We then show that the connection-level throughput region of such multi-path routing/congestion control algorithms can be larger than that of a single-path congestion control scheme.
 

References