International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

LGDSTR: Local Greedy Distributed Spanning Tree Routing by Reducing Local minima in higher dimensional space

Anandhi.R1, Dr.R.Manicka chezian2
  1. Research scholar, Department of Computer Science, Nallamuthu Gounder Mahalingam College, Pollachi, India
  2. Associate Professor, Department of Computer Science, Nallamuthu Gounder Mahalingam College, Pollachi, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

LGDSTR is an improvised GDSTR with an additional Greedy-Hull forwarding to prevent loops and incorporates local information to improve routing and geocast performance in dense networks. Overheads incurred by routing protocols diminish the capacity available for relaying useful data over a mobile wireless ad hoc network. Discovering and understanding the lower bounds on the amount of protocol overhead incurred for routing data packets is important for development of efficient routing protocols, and for understanding the actual (effective) capacity available for network users. In this use an information-theoretic approach for characterizing the minimum routing overheads of geographic routing in a mobile network. We formulate the minimum overhead problem as a rate-distortion problem. The formulation may be applied to networks with arbitrary traffic arrival and location service schemes. We evaluate lower bounds on the minimum overheads incurred for maintaining the location of destination nodes and consistent neighborhood information in terms of node mobility and packet arrival process. In this paper we discuss to characterize the deficit caused by the routing overheads in the overall transport capacity of a mobile network, performance evaluation comparison in hop stretch and path stretch metrics of LGDSTR with GDSTR and ALBA-R.

Keywords
ALBA-R, convex hull, GDSTR, LDSTR, greedy-hull, spanning tree

INTRODUCTION
In Geographic routing each node can determine its own location and that the source is aware of the location of the destination. With this information a message can be routed to the destination without knowledge of the network topology or a prior route discovery Route selection in some routing algorithm is done by selection on multiple metric by combining them in single metric. Several routing metric are used to achieve efficient routing in various geographic routing protocols. Some problems are identified among the routing protocols namely, Greedy routing is simple and it does not provide delivery guarantee, On the other hand MFF routing provides delivery guarantee but is complicated and may create very inefficient path and finally Cost for planarization and unavailability of location information are major issues in deployment of geographic routing. Several geographic routing related protocols are implemented to achieve good coordinate when location information is not available. GDSTR (Greedy Distributed Spanning Tree Routing) switches to routing on a spanning tree instead of a planar graph when packets end up at dead ends during greedy forwarding. To choose a direction on the tree that is most likely to make progress towards the destination, each GDSTR node maintains a summary of the area covered by the sub tree below each of its tree neighbors using convex hulls. This distributed data structure is called a hull tree. GDSTR not only requires an order of magnitude less bandwidth to maintain these hull trees, it often achieves better routing performance than other planarization-based geographic routing algorithms.

RELATED WORK
H. Takagi et al.,(1984) [2]in this paper multihop packet radio networks with randomly distributed terminals, the optimal transmission radii to maximize the expected progress of packets in desired directions are determined with a variety of transmission protocols and network configurations. B.N. Clarket et al., (1990)[3] this paper Unit disk graphs are the intersection graphs of equal sized circles in the plane: they provide a graph-theoretic model for broadcast networks (cellular networks) and for some problems in computational geometry. E. Kranakis et al., (1999)[5] Proposed a routing algorithm called a local routing algorithm to find the starting point and location of the destination. P. Bose et al., [6] in this paper routing problems in ad hoc wireless networks modeled as unit graphs in which nodes are points in the plane and two nodes can communicate if the distance between them is less than some fixed unit. K. Seada et al., [7] in this paper absence of location errors, geographic routing using a combination of greedy forwarding and face routing has been shown to work correctly and efficiently. Y.-J. Kim et al.,(2005) this paper Geographic routing has been widely hailed as the most promising approach to generally scalable wireless routing. However, the correctness of all currently proposed geographic routing algorithms relies on idealized assumptions about radios and their resulting connectivity graphs. [7] Q. Fang et al., (2006) In real sensor network deployments, spatial distributions of sensors are usually far from being uniform [8]. P. Casari et al., (2007)[6] in this paper Geographic forwarding in wireless sensor networks (WSN) has long suffered from the problem of bypassing "dead ends," i.e., those areas in the network where no node can be found in the direction of the data collection point (the sink). Z. Li, R. Li, Y. Wei (2010) Localization is one of the key techniques in wireless sensor network. The location estimation methods can be classified into target/source localization and node self-localization. In target localization, mainly introduce the energy-based method. [4]A. Camillo et al., (2013) presents IRIS, an integrated interest dissemination and convergecasting solution for wireless sensor networks (WSNs). The interest dissemination protocol is used to build and maintain the network topology and for task/instruction assignment.[5] S. Ruhrup et al., (2013) in this paper beaconless or contention-based geographic routing algorithms forward packet towards a geographical destination reactively without the knowledge of the neighborhood.[9] Such algorithms allow greedy forwarding. Anandhi.R, R.Manicka chezian(2014) presents an Overview of geographic routing protocols in wireless sensor network. In WSN, the state required to be maintained is minimum and low overhead, in addition to their fast response to dynamics. [1]

GDSTR OVERVIEW
Greedy Distributed Spanning Tree Routing (GDSTR) describes hull trees, used for routing, and how they are built and maintained. It also describe how hull trees can be used to implement geocast and approximate routing and improved GDSTR, a variant of GDSTR that achieves superior routing performance for dense networks with small voids. Like previous geographic face routing algorithms, GDSTR forwards packets using simple greedy forwarding whenever possible. It switches to forwarding on a spanning tree only to route packets around voids, and escape from a local minimum.[11] It switches back to greedy forwarding as soon as it is feasible to do so. The reason GDSTR is able to guarantee the delivery of packets in a connected network is that the tree traversal forwarding mode is guaranteed to deliver the packet to any node in the network without greedy forwarding.
A spanning tree that contains all n nodes in a network, we can successfully deliver a packet to any node in the network by traversing the tree in a manner similar to a depth-first search. This traversal requires no state to be stored in the packet and guarantees that a packet will be delivered in no more than 2n - 3 hops. If the specified destination is not found in the tree, then we can terminate the traversal in exactly 2n - 2 hops if stored information about the starting node in the packet. A major contribution of proposed work is the definition of a new distributed data structure, an augmented spanning tree that we call a hull tree, that allows to restrict the above search problem to a small sub tree of the full spanning tree for a given destination, thereby guaranteeing packet delivery in much fewer than 2n - 3 hops.

HULL TREES
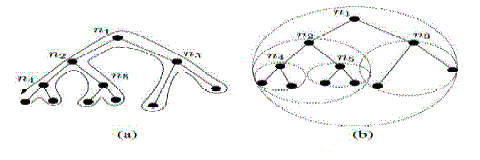
A hull tree is a spanning tree where each node has an associated convex hull that contains the locations of all its descendant nodes. Hull trees provide a way of aggregating location information and they are built by aggregating convex hull information up the tree. This information is used in routing to avoid paths that are not productive; instead we traverse a significantly reduced subtree, consisting of only the nodes with convex hulls containing the destination point.[12]
Each node in basic hull tree stores information about the convex hulls that contain the coordinates of all the nodes in subtrees associated with each of its child nodes specified in Figure 1. The convex hull information is aggregated up the tree. Each node computes its convex hull from the union of its coordinate and the points on the convex hulls of all its child nodes, and this information is communicated to the parent node. Consequently, the convex hull associated with the root node is the convex hull of the entire network and contains all the nodes in the network.

SPANNING TREE CONSTRUCTION
After evaluating a number of spanning tree algorithms, found that the minimal-depth tree yields the best routing performance. The minimal-depth tree is constructed by having each node choose the neighbor with the minimal number of hops to the root as its parent. When a node has a choice between multiple neighboring nodes that are the same number of hops from the root, the nearest node is chosen preferentially. [13]
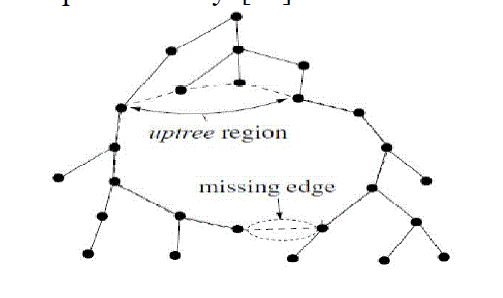
With hindsight, it is not surprising that the minimal-depth tree yields the best routing performance. Firstly, the minimaldepth tree tends to choose the shorter links preferentially. Refer to the example in Figure 2 it should be clear that shorter links reduce the occurrences of crossing links.
The region of the void nearest to the root called the uptree region. In this region, the edges of the void are not edges in the hull tree and hence routing around this region involves routing up and down the tree. For the remaining parts of the void, all the edges (except one) are part of the min-depth tree. Because the min-depth tree yields the shortest paths between each node and all of its ancestor nodes, tree traversal is efficient along these regions. Because spanning trees do not contain cycles and yet must contain all nodes in the network, there is exactly one edge on the far side of the void from the root that is not an edge in the tree. We call this the missing link. This missing edge restricts packet forwarding along the void using this hull tree to only one direction. Given two hull trees, we observe that as long as the two trees do not share the same missing link, they will together allow the void to be traversed in both directions (clockwise and counterclockwise) around the void. To increase the probability of generating hull trees that cover disjoint regions of the void, an approach is to set their roots at opposite ends of the network.

PROPOSED GDSTR
GDSTR works well for sparse networks with large voids. For dense networks, geographic face routing algorithms can achieve better performance since the voids tend to be small and it generally does not matter which forwarding direction is picked. The is because when there are many hops between the root of the hull trees and the leaves, the hull trees are not able to approximate voids quite as well as planar faces and GDSTR therefore incurs additional routing overhead. Also, geocast is expected to be less efficient when the hull tree is large.
One possible approach would be to use GDSTR in sparse networks and geographic face routing algorithms in moderately dense networks. However, such an approach does not address the high maintenance costs of planarizing the network graph. Another issue is that large networks are likely to be heterogeneous, with some dense regions and some sparse regions. Ideally, a good geographic routing algorithm should work well in networks of all densities. The proposed system improved GDSTR, a variant of GDSTR that incorporates local information to improve routing and geocast performance in dense networks.
A. Overview:
The key idea in improved LGDSTR is to augment GDSTR with two forests of local Trees and an additional greedy-hull forwarding mode. In LGDSTR, a node will first attempt to forward a packet greedily as before. If greedy forwarding fails, it will switch to the new greedy-hull forwarding mode by using the information contained in the convex hulls of a local hull tree. By local, we mean that the tree contains only the nodes in a limited locality. Since correctness cannot be guaranteed, only forwarding depicted.
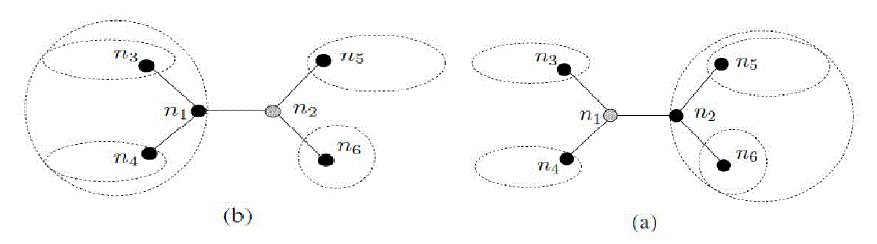
Can sometimes fail using the local tree and in such a case, a node will switch to forwarding on one of the two original global hull trees, which is guaranteed to succeed. In order to implement greedy-hull forwarding, the local hull trees employ a different convex hull aggregation algorithm than that employed by GDSTR to maintain global hull trees. This new aggregation mechanism presents a node with a view of the locations accessible via each neighboring node. To aggregate hulls this way, each node broadcasts the hulls of all its neighbors instead of its own hull. Illustrate the local hull tree aggregation algorithm with the example shown in Figure 3. In particular, the convex hull associated with each neighbor contains the set of destination points that are reachable through that neighbor. In this example, both nodes n1 and n2 have three neighbors. In Figure. 3(a), show the convex hulls from n1's perspective. Under this new scheme, n2's keepalive message will contain the hulls for n1, n5 and n6 from its perspective. From n1's perspective, its convex hull for n2 is the convex hull that contains n2 and the convex hulls for n5 and n6.
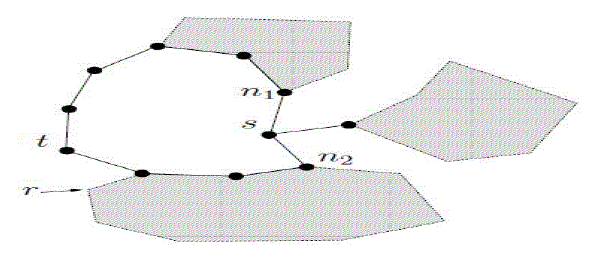
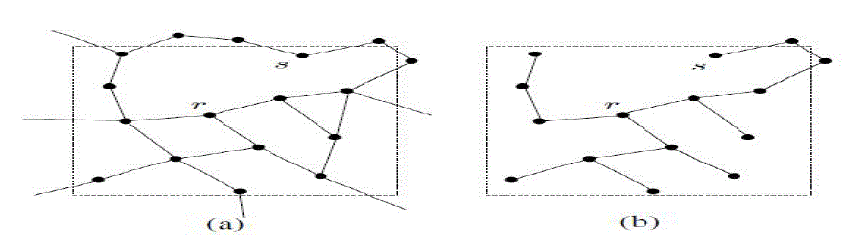
In Figure 3(b), from n2's perspective, its convex hull for n1 is the convex hull that contains n1 and the convex hulls for n3 and n4. This provides each node with a view of the geographic coordinates accessible via each neighboring node in the tree. In Figure 4, node s receives a packet with destination t and has to decide how to forward the packet. Since node s is a dead end for greedy forwarding, it tries to forward the packet in greedy-hull forwarding mode. In this mode, node s considers the convex hulls of its neighboring nodes and finds the point on the hulls that is closest to the destination t. It turns out to be point r on the convex hull of node n2. Hence, node s forwards the packet to n2 instead of n1. Like GDSTR, the coordinate of the node at which a packet switches to greedy-hull forwarding mode is recorded as nmin and a packet will revert to greedy forwarding mode as soon as if it switches to greedy mode. In the former case, a packet will switch to GDSTR tree traversal mode on one of the two available global trees. phull is only updated with a value that is monotonically nearer to the destination. If a packet in greedy forwarding mode ends up in a dead end and the associated node does not have a convex hull that has a point that is closer to the point phull, the packet will bypass the greedy-hull forwarding mode and switch directly to tree traversal on one of the two global trees. This is to prevent oscillations.
B. LOCAL TREES GDSTR:
To construct the local hull trees, divide the coordinate space into a square grid of fixed length, and all the nodes within each grid square will be members of the same local tree. The root of a local tree is the node with a coordinate that is closest to the center of a grid square. The process of building such a tree has two steps: first, a node attempts to route a packet to the center of its local grid square. Doing so will allow it to identify the root node of its local tree. Next, it determines its parent by routing a packet to the root node. The second step is necessary because a given node may not be connected to the root of its hull tree through neighbors that are within the same grid square. This is illustrated in the example shown in Figure 5(a). In this example, node r is the root of the local hull tree since it is nearest to the center of the square grid; node s is however connected to neighbors that are outside the square grid. The resulting local hull tree is shown in Figure.5 (b). This example also shows that it is possible for nodes near the edge of a grid square to be members of the local hull trees of neighboring grid squares. The strict membership condition imposed that all the nodes within each grid square belong to the same local hull tree to provide correctness guarantees for geocast.

PERFORMANCE EVALUATION
The proposed goal is to compare the basic algorithmic behavior of LGDSTR to other geographic routing algorithms. Routing performance is measured with respect to two metrics: i) path stretch ii) hop stretch Path stretch is the ratio of the total path length to the shortest path (in Euclidean distance) between two nodes; hop stretch is the ratio of the number of hops on the route between two nodes to the number of hops in the shortest path (in terms of hops). Performance evaluation is measured in terms of:
1) Effect of Network Density 2) Effect of Network size. 3) Effect of Obstacles. Typically, GDSTR uses only two global hull trees. To understand the tradeoffs, we compare the performance of LGDSTR with one and two local trees (in addition to two global trees) to that for GDSTR with two to four global hull trees to determine whether we would see the same performance for GDSTR with three or four global trees.
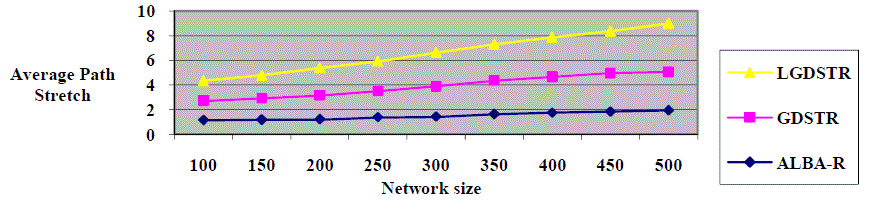
In particular, we see that LGDSTR achieves better routing performance than GDSTR and ALBA-R. LGDSTR is able to surpass the routing performance of both GDSTR and LGDSTR. For 500-node networks, LGDSTR with two local hull trees achieves a 17% improvement in stretch over GDSTR (with two global hull trees) and 8% lower stretch than ALBA-R.
Finally, LGDSTR is able to achieve up to a 17% improvement in stretch performance over GDSTR and an 8% lower stretch than ALBA-R, the best existing face routing algorithm, for dense networks with small voids. We have also shown than we can implement geocast with 10% less overhead with LGDSTR hull trees when compared to that for GDSTR (with two hull trees). Furthermore, our algorithm will likely require no more than twice the minimum number of messages for networks smaller than 500 nodes in size.

CONCLUSION
This paper explains the improved performance of LGDSTR in the metrics of hop stretch and path stretch. It is more efficient than other routing algorithm of GDSTR and ALBA-R. The underlying intuition for geographic routing is that the physical location of a node relative to the destination of packet provides a good hint of the correct general forwarding direction. While LGDSTR is currently implemented over three dimensional Cartesian coordinates, it is generalizable to coordinates in higher dimensional spaces, since convex hulls are specialized to higher dimensions. Finally LGDSTR can achieve better routing stretch in higher dimensional space. The challenges attain by the local GDSTR reduces Local Minima in 3D,Packet delivery guaranteed, Hop stretch close to 1, Out performs 2D in both performance and cost, Scales well to network up to 500 node.
 

Tables at a glance
Table icon Table icon
Table 1 Table 2
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 1
Figure 1 Figure 2 Figure 3 Figure 4
Figure 2 Figure 3 Figure 4
Figure 5 Figure 6 Figure 7
 

References