Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

LMI APPROACH FOR ROBUST CONTROL OF SYSTEM WITH UNCERTAINTY IN TIME DELAY

Shyma Muhammed1, Dr. Abraham T Mathew2
  1. Research Scholar Department of Electrical Engineering, National Institute of Technology, Calicut, India
  2. Professor Department of Electrical Engineering, National Institute of Technology, Calicut, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Control of time delay systems has been a challenging problem for the control engineers. The issues have been inviting attention of many researchers, especially in the context of robust control. This is further motivated by the fact that many processes have the time delay present in the corresponding models and thus the design of controller becomes computationally rather involved. Time-delayed systems are pervasive in many engineering systems such as tele-robotic systems, vehicle platoons, biological systems, chemical processes etc. The presence of delay in these systems makes closed-loop stabilization difficult and degrades tracking performance. The problem becomes extremely difficult when uncertainties are present in the model as well as in the delay parameter. It is known that, in general, the delays appear in the system models due to various factors like transport phenomena, computational time needed for generation of control command, time delay in the smart measurement devices, approximation of a higher order system with a lower order model etc. This paper is concerned with the robust control of linear varying time delay system using LMI approach. Also this paper develops a control technique for uncertain linear time delay systems in which both plant uncertainty and controller uncertainty are taken into account.

Keywords
LMI control, time delay system, robust control, uncertainty, stability.

INTRODUCTION
Time delays are usually unavoidable in many mechanical and electrical systems. The presence of delay typically imposes strict limitations on achievable feedback performance in both continuous and discrete systems. As it is seen, time delay is very often encountered in various technical systems, such as electric, pneumatic and hydraulic networks, chemical processes, long transmission lines, robotics, etc.[1]. The existence of pure time lag, regardless if it is present in the control or/and the state, may cause undesirable system transient response, or even instability. Consequently, the problem of controllability, observability, robustness, optimization, adaptive control, pole placement and particularly stability and robust stabilization for this class of systems, have been matter interests for the scientists and researchers during the last several decades [2]. The delay usually results from the physical separation of the components and typically occurs as a delay between the change in the manipulated variable and its effect on the plant or a delay in the measurement of the output. This means, we find a time delay between the instant of occurrence of an event in time and the measurement of it has been made to the extent needed. Dead-time elements are needed for accurate modelling of such systems [3]. Digital computers in control system also introduce the necessity of dead-time elements to model the computational delay inherent in the systems. The presence of the delay complicates the design process as it makes continuous systems to be infinite dimensional and it significantly increases the dimensions in discrete systems [4].
In the process-control field where manipulation of physical variables like pressure, flow, liquid-level, temperature etc are needed, the systems are sluggish and we find the time delay in signal flow between the sub-systems handling such process variable. These factors cause the dead-time effects [5]. Even where a pure dead-time element is not present the complexity of the process will often result in a response, which has the appearance of a pure dead-time element due to higher order of the system dynamics. Modelling of such complex systems is a very difficult task. However many years of experience and decades long research by control scientist across the world have proved that the controllers based on approximate process models are quite versatile. But, efforts are still continuing to design new controllers that would simultaneously satisfy robust stability and robust performance, when modelling uncertainty, input disturbances, setpoint changes and the parameter uncertainty are present.
Again, in systems that involve critical missions (such as aircraft, chemical process control systems) time-delay often appears either in the state, the control input, or the measurements [6]. Unlike ordinary differential equations or simple transfer functions, such systems are infinite dimensional in nature and could be unstable and of non-minimum phase nature in the frequency domain [7]. Precisely, there could be uncertainty in time delay also. The issues in stability and performance of control systems with uncertainty in delay are, therefore, both of theoretical and practical importance. During the past few decades, many researchers have put significant efforts in the analysis and synthesis of uncertain systems with time-delay. Various techniques have been proposed dealing with the time delays, finite-dimensional sufficient conditions for stability and stabilization, based on the Lyapunov stability etc [8]. Departing from the classical linear finite dimensional techniques which apply Smith Predictor type designs, the new methods simultaneously allow for delays in the state equations and for uncertainties in both the system parameters and the time delays. During the early stages, delay independent results were obtained which guarantee stability and prescribed performance levels of the resulting solutions. Recently, delay-dependent results have been derived that considerably reduce the over design entailed in the delay independent solution. Different methods have been proposed for the control of time delay systems [9-10] but they are either too complex for an industrial implementation or they fail to control unstable systems with very long delays.
In this paper a linear matrix inequality (LMI) approach for the control of varying time delay system and an uncertain linear time delay system are proposed. The efficacy of the proposed controller is validated using numerical examples. In our previous work in time delay system using modified smith predictor controller [11], the controller is sensitive to changes in root location, delay etc. But in this proposed method using LMI techniques, the controller is not sensitive to time delay. Unlike the methods in [9-10] this proposed method is applicable to systems with very long delays
The remaining part of the paper is organized as follows: Section II deals with system description and problem formulation of both linear and uncertain time delay systems. Section III deals with the design methodology Section IV is devoted to present numerical examples. Section V gives the simulation results and the analysis of it. Finally Section Vl concludes the paper, followed by the references used.

II.SYSTEM DESCRIPTION AND PROBLEM FORMULATION
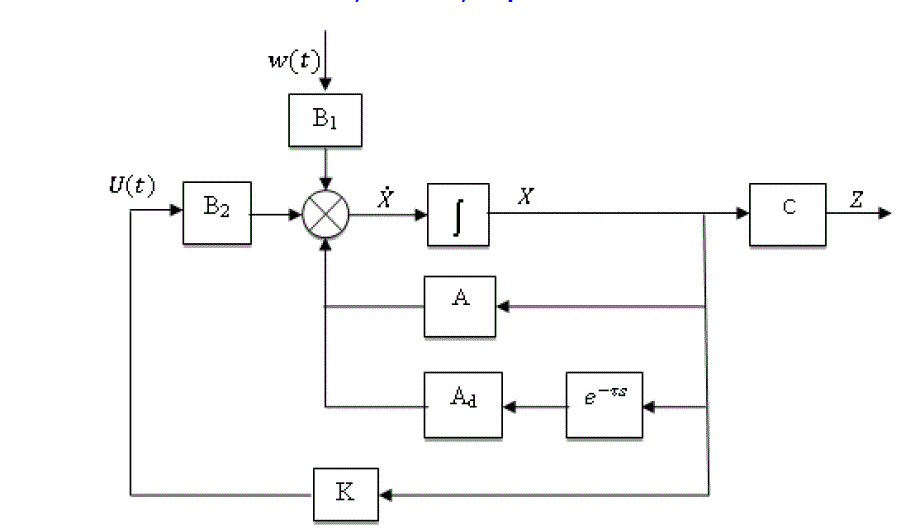
Consider a continuous linear varying time delay system described by the state equation
image

III. DESIGN METHODOLOGY
First we can find the linear matrix inequality for the system (1) with the control input and the external disturbances as
zeros. Then the state Eqn (1) reduces to a homogeneous system given by
image
image
image
image
image

IV. SIMULATION RESULTS AND DISCUSSION
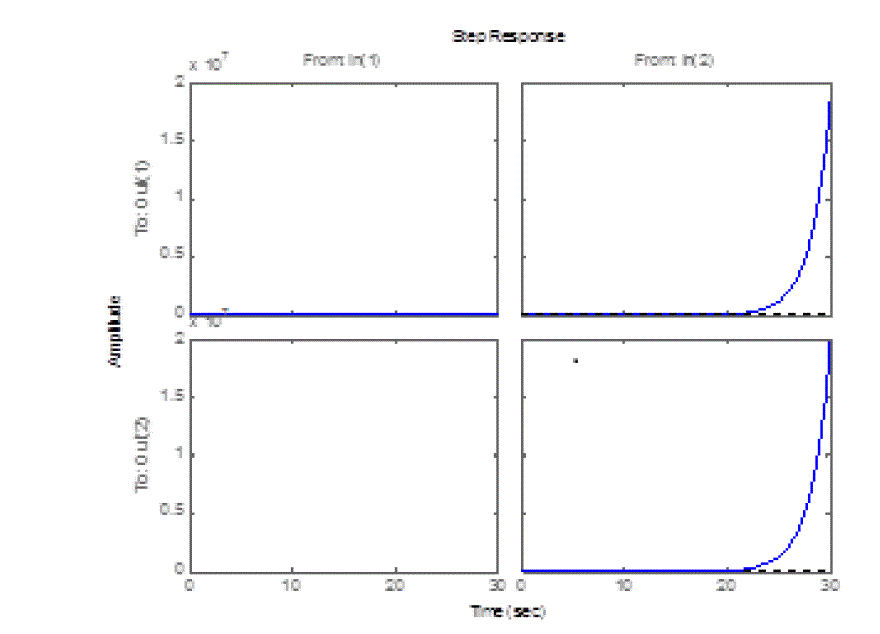
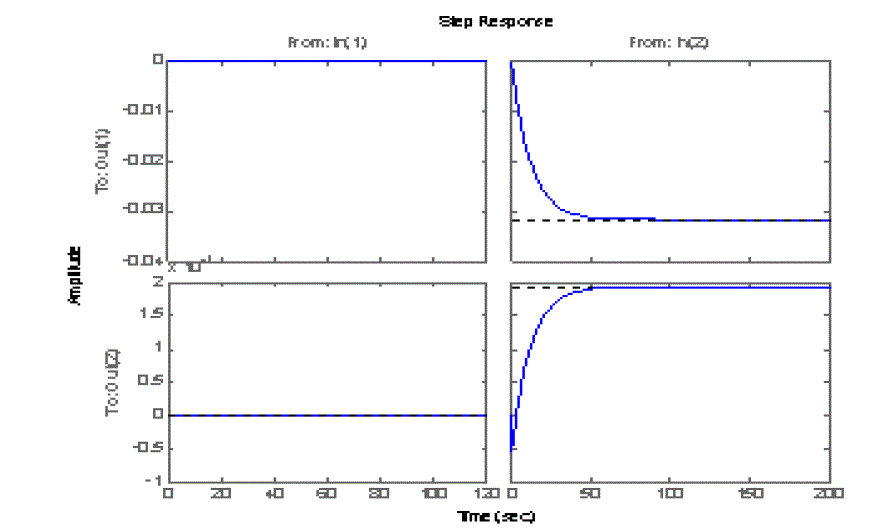
The controller was synthesized as mentioned above with the help of LMI solvers [15] .Fig 2 shows the open loop response of the system(1) with time delay 0.1 sec whereas Fig 3 shows the closed loop response of the same system with same time delay. From these figures it can be seen that the given system is unstable without the controller and is stable with the proposed LMI controller. From fig 3 it can be seen that when the time delay is 0.1 sec, the settling time is 47 sec and the steady state errors are -0.0317 & 0.00194 respectively.Then increased the time delay to different values from 1 sec to 190 sec and found out the corresponding maximum settling time and steady state errors. As in the previous case here also it can be seen that the system is unstable without the controller and is stable with the controller. Table 1 gives the Performance specification of the system represented by Eqn(1) with different values of time delay.
In Table 1, column (1) shows the time delay. It has been assumed that the time delay would change from 0 to 190 sec .Column (2) shows the corresponding values of the settling time and column (3) shows the corresponding steady state error. It can be seen that as the time delay is increased from 1 sec to 10 sec, the settling time is changed from 49.5 sec to 78 sec but the corresponding steady state errors remains the same. Again it can be seen that when the time delay is increased to 20 sec and 100 sec, then the corresponding settling time are 114 sec and 428 sec respectively. we can see that, when the time delay is increased to 160 sec , the settling time is reduced to 204 sec and the steady state error reduces -0.0281& 0.00125 respectively. From the Table 1 it can be seen that as the time delay increases the settling time also increases and after a particular delay it decreases. Again we can see that at higher values of delay, the steady state error becomes zero or approaches to zero. The non-zero error remains constant at large values of delays.
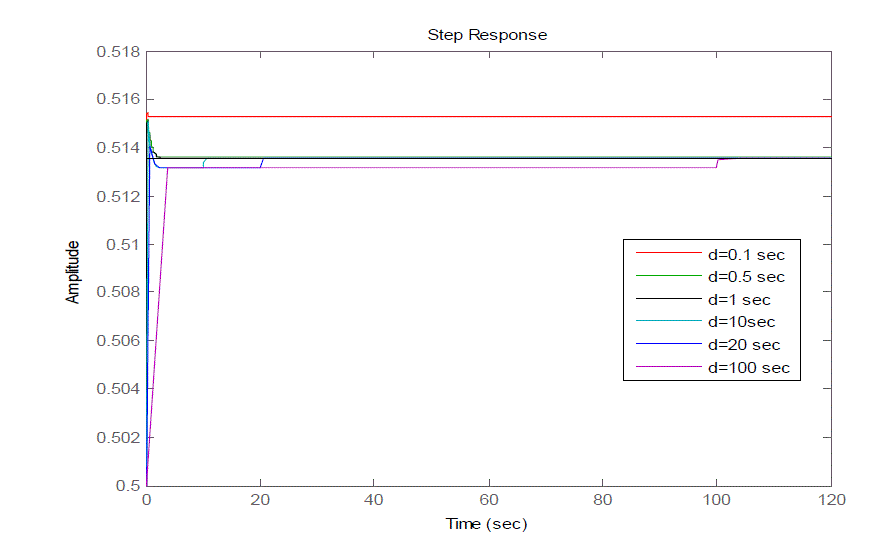
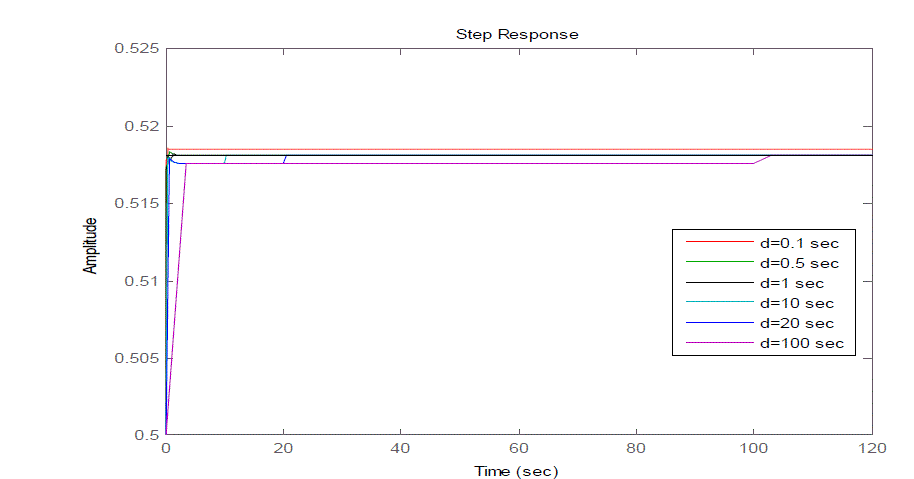
Fig 4 and Fig 5 shows the closed loop response of the given uncertain system (2) for different values of delay with disturbance attenuation bound () 1 and 0.5 respectively. It can be seen that as the value of  increases the steady state error decreases but the settling time increases.
Fig 4 show the closed loop responses of the given uncertain system having the disturbance attenuation bound 1 with different delays say 0.1 sec,0.5 sec,1 sec,10 sec,20 sec& 100 sec respectively. From Fig 4 it can be seen that the steady state error is high for a delay of 0.1 sec whereas it is small for a delay of 100 sec.
Fig 5 show the closed loop responses of the given uncertain system having the disturbance attenuation bound 0.5 with different delays say 0.1 sec,0.5 sec,1 sec,10 sec,20 sec& 100 sec respectively. Here also it can be seen that the steady state error is high for a delay of 0.1 sec whereas it is small for a delay of 100 sec. Again it can be infer that as the value of  increases the overshoot of the output response also increases.

CONCLUSION
In this paper the LMI control of a linear varying time delay system was discussed. Again a robust ��∞ controller is developed for linear time delay systems subject to uncertainties in both plant and controller. The robust controller is obtained using an LMI algorithm. The LMI solvers in MATLAB® were made use of for solving the inequalities [16].The analysis of the system with varying time delay was also performed. In the case of linear varying time delay system it can be seen that as the time delay increases the settling time also increases. But after a particular delay, settling time decreases. Again we can see that at higher values of delay, the steady state error becomes zero or approaches to zero. The non-zero error remains constant at large values of delays. In the case of uncertain time delay system it can be seen that the steady state error is high for small delay whereas it is small for large delays. Again it can be infer that as the value of disturbance attenuation bound increases the overshoot of the output response also increases. The proposed LMI controller would give good performance to systems with uncertainty in time delay.

Tables at a glance
Table icon
Table 1
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
 

References