Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Localization of Phase Spectrum Using Modified Continuous Wavelet Transform

Dr Madhumita Dash1 , Ipsita Sahoo2
  1. Professor, Department of ECE, Orisaa Engineering College, Bhubaneswr, Odisha, India
  2. Asst. professor , Department of ECE, Orissa Engineering College, Bhubaneswar , Odisha , India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

In recent years, there has been an increasing interest with respect to using a set of orthonormal bases of wavelets for multiresolution approximation of a function     2 f x L . This Paper presents a new transform for detection of phase change using the analysis functions which are obtained by dilation of a spline window and is frequency dependent. This paper also enables the present transform to “zoom in” on singularities and makes it very attractive for the analysis of non-stationary signals and the other advantage of this technique is that spline functions are more localized than the Gaussian function which is used in WFT.

Keywords
Orthonormal bases , Wavelets , Multiresolution Approximation , Phase change , Spline window , Non- Stationary , Gaussian function

INTRODUCTION
Signal processing has played an important role in different engineering applications. Early developments have treated image processing as more of arts than science, but with the time, recent algorithms for different vision systems require strong mathematical support for the better performance of such systems for a variety of images. Eminent signal processing researchers have claimed that a signal contains information at different scales. The notion of “Scale” is being used by signal processors while the notion of “Resolution” is frequently associated with the image processing literature. A signal or an image can be decomposed into different scales in the spatial domain. This time-scale or spacescale representation of a signal is commonly known as multiresolution signal analysis. Wavelet transform [1] has played an important role in signal processing for detection of local details from a non-stationary signal. However, detection of a change in the absolute phase of a constituent frequency of a ‘non-stationary’ signal is not possible by using the Windowed (or short-time) Fourier Transform (WFT) and the Continuous Wavelet Transform (CWT) [2]. This has developed a modified CWT to supplement both WFT and CWT, which are treated as two fundamental tools in signal processing. A new transform for detection of phase change. In this case, the analysis functions are obtained by dilation of a spline window which is frequency dependent. This property enables the present transform to “zoom in” on singularities and makes it very attractive for the analysis of non-stationary signals. Another advantage of this technique is that spline functions are more localized than the Gaussian function which is used in WFT. It is well known from the wavelet literature that WFT and CWT can be used for time-frequency localization of non-stationary signals[3]. But they do not provide us phase information of a signal. On the other hand, the proposed modified CWT will provide phase information efficiently. This shows a distinct improvement over the WFT and CWT. From Fig.1 it is seen that the phase information is localized. This reveals the suitability and effectiveness of the proposed transform for analysis of non-stationary signals. The proposed transform may be useful for different signal processing applications [5].

II. THE WAVELET TRANSFORM
Wavelet transforms are useful to extract local details from “non-stationary” signals [1]. There are two different types of wavelet transforms –
(A) The continuous wavelet transform and
(B) The discrete wavelet transform.

A .The Continuous Wavelet Transform
The continuous wavelet transform (CWT) provide us a similar type of time-frequency description discussed in the preceding section with few very important differences . The CWT is defined as :
The functions a,b  are called wavelets. Note that the function  is called as the mother wavelet.
In the case of CWT two index are used :
It is noteworthy to mention here that both  and ‘g’ are real.

B .The Discrete Wavelet Transform
The discrete wavelet transform (DWT) can be derived from Eq. (1.15) (defined for CWT) by restricting ‘a’ and ‘b’ to have only discrete values :
Proper choice of a 0 , b 0 and  a,b constitute an orthonormal basis set for different signal and image processing applications

III. THE MODIFIED WFT & CWT
Let g(k) represent a discrete signal and let w(k) denote a window sequence. Then the WFT of g(k) is defined as :
where and n=0,1,…., N-1. Note that
represent the discrete Fourier transform of the particular portion of the signal .
The CWT of g(k) is defines as :
where b is a scale parameter and  is a Gabor-wavelet obtained through modulation of a window function w(x) given as
(2)
Note that w(x) is the Gaussian function given by
(3)
The Gaussian window by a symmetrical B-spline window. It may be noted that B-spline windows provide a compact support and closely approximates a Gaussian window [9]. A centred B-spline function of degree n can be generated by evaluating (n+1)-fold convolution of a unit rectangular pulse. The corresponding discrete B-spline window with an additional resolution factor ‘m’ can be obtained by enlarging the spline function of degree n, i.e, n(x) by an integral factor m and sampling at the integers.
(4)
Note that ‘m’ is the resolution factor. The resulting complex B-spline wavelet can be explicitly written as :
(5)
This is not surprising to claim that the time-frequency localization of this function is improved rapidly with the degree as it converges to a Gaussian function. The resolution factor m to be an inverse function of the frequency of the signal being localized. Thus,
(6)
Since the effective width of the B-spline window is a function of the frequency f, the phase information can be extracted (with full information about the complex phase at each frequency component). This shows a definite improvement over the existing CWT & WFT techniques. The amplitude and phase spectra are given by
(7)
Note that W is the new modified CWT.

.IV. RESULTS AND DISCUSSIONS
Both time and frequency resolutions are fixed in the case of Windowed Fourier Transform (WFT) and short-time Fourier transform (STFT). Hence, the WFT or STFT approach is particularly suitable for the analysis of signals with slowly varying periodic or stationary characteristics. The wavelet transform provide us a time-scale analysis [1] and they have shown high performance to detect local details from non-stationary signals (or transient signals). However, they do not provide us a precise scale-frequency analysis for transient signals. Center frequencies of band-pass filters connected with wavelets are fixed and depend upon the scale parameter. Hence, wavelet analysis is not very attractive for harmonic analysis of distorted signals. The discrete transform introduced in this Section may be treated as the projection of the time-series {g(k)} onto a space consisting of orthonormal basis vectors. The time-frequency localization of a signal can be achieved by using the proposed transform efficiently. The proposed transform can be evaluated by using the following algorithm:

Algorithm :
Step 1 :Find the Fourier transform of the B-spline window using Eq.(5).
Step 2 :Find the Fourier transform of the given discrete-time signal {g(k)} (with N number of data points & unit sampling) by using FFT.
Step 3 :Shift the B-spline window spectrum with index l & multiply with the Fourier transform of the given discretetime signal.
Step 4 :Find the inverse Fourier transform of the product to produce the row of the transform matrix W corresponding to a constituent frequency ‘n’.
Step 5 : Repeat steps 3 & 4 till one gets all rows of W matrix.
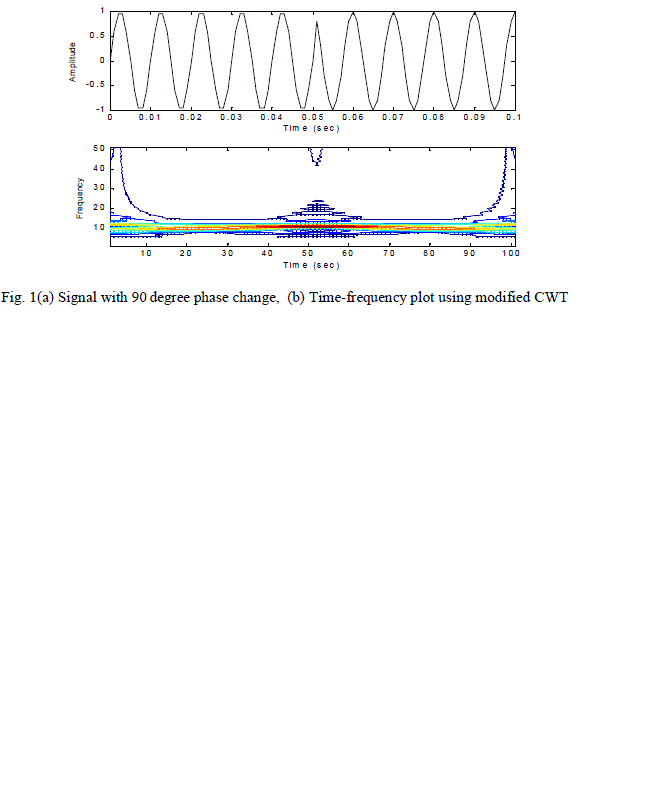
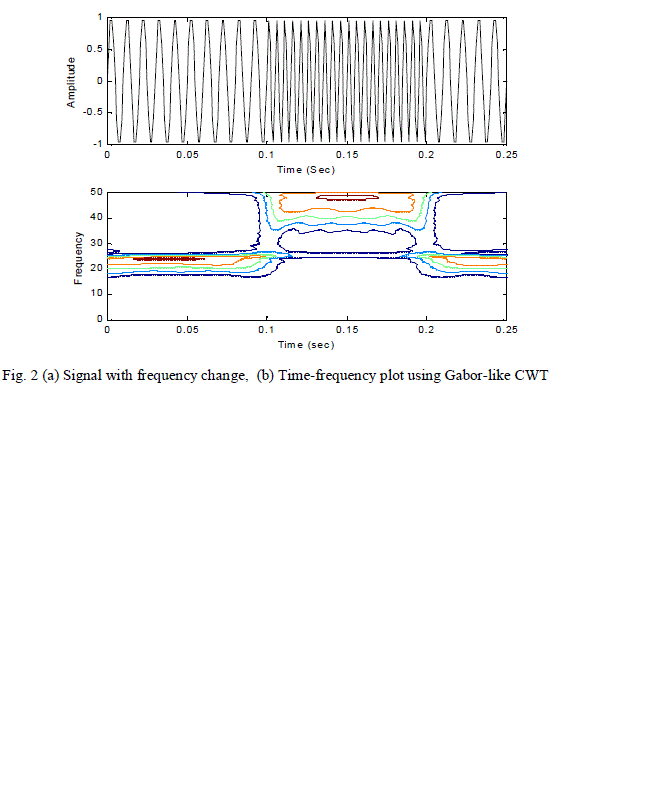
The proposed algorithm has been used to find the new transform matrix W for different signals. Two different signals to highlight the power and usefulness of the proposed transform. A sinusoidal signal with a phase change at time t=0.05 sec has been shown in Figure 1 (a) and its Time-frequency plot has been shown in Figure 1(b). From figure1 , it is seen that the phase change in the original signal is detected accurately. Figure 2(a) represents a signal with change in frequency of the signal from 100 Hz to 200 Hz during time interval 0.1 to 0.2 sec. The time-frequency plot of the frequency changing signal has been shown in Fig 2(b), which clearly shows the superiority of the proposed method for detection of frequency change as well.

V. CONCLUSION
This paper deals with a modified Gabor-like Windowed Continuous Wavelet Transform (CWT) for localization of phase spectrum. This proposed transform provide a frequency-dependent resolution while maintaining a relationship with the Windowed Fourier Transform (WFT) and Continuous Wavelet Transform (CWT), hence useful for multiresolution signal analysis. Here a localized scalable B-spline window has been used for dilation and translation while keeping modulating sinusoids fixed along the time axis. It is interesting enough to note here that the distinctive frequency-dependent resolution features are absent in both WFT and CWT.

Figures at a glance
Figure 1 Figure 2
Figure 1 Figure 2
 

References