Keywords
|
| Log Linear Model, Parameter Estimation, Query Reformulation, Spelling Error Correction, String Transformation |
INTRODUCTION
|
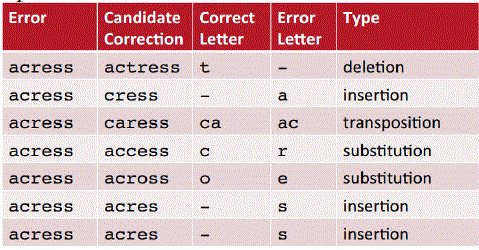
| String transformation can be formulated to natural language processing, pronunciation generation, spelling error correction, word transliteration, and word stemming. String transformation can be defined as given an input string and a set of operators, one can able to transform the input string to the k most likely output strings by applying a number of operators. Here the strings can be strings of words, characters, or any type of tokens. Each operator is a transformation rule that defines the replacement of a substring with another substring. String transformation can be performed in two different ways, depending on whether or not a dictionary is used. In the first method, a string consists of characters. In the second method, a string is comprised of words. The former needs the help of a dictionary while the latter does not. Spelling errors is of two steps. 1) Non word errors and 2) Real word errors. Non word errors are those words not in dictionary.. Spelling errors in queries can be corrected in two steps: (1) Candidate generation and (2) Candidate selection. Fig 1.shows the spelling error correction in word processing. Candidate generation is used to find the words with similar spelling, from the dictionary. In a case, a string of characters is input and the operators represent insertion, deletion, and substitution of characters with or without surrounding characters. |
| They are done by using small edit distance to error. Candidate generation is concerned with a single word; after candidate generation, the words in the context can be further leveraged to make the final candidate selection,[1], [2]. Query reformulation in search is aimed at dealing with the term mismatch problem. For example, if the query is “MCH” and the document only contains “MC Hospital”, then the query and document do not match well and the document will not be ranked high. Query reformulation attempts to transform “MCH” to “Medical College Hospital” and thus make a better matching between the query and document. In the task, a query has been (string of words), system needs to generate all similar queries from the original query (strings of words). The operators are transformations between words in queries such as “ex”→“example” and “carrying ”→“holding” [3]. Previous work on string transformation can be categorized into two groups. Some task mainly considered efficient generation of strings, assuming that the model is given [4]. Other work tried to learn the model with different approaches, such as a generative model [5], a logistic regression model [6], and a discriminative model [7]. There are three fundamental problems with string transformation: (1) how to define a model which can achieve both high accuracy and efficiency, (2) how to train the model accurately and efficiently from training instances, (3) how to efficiently generate the top k output strings given the input string, with or without using a dictionary. |
| In this paper, we propose a probabilistic approach to the task. Our method is novel and unique in the following aspects. It employs (1) a log-linear (discriminative) model for string transformation, (2) an effective and accurate algorithm for model learning, and (3) an efficient algorithm for string generation. The log linear model defined as a conditional probability distribution of an output string and a rule set for the transformation given an input string. The learning method is based on maximum likelihood estimation. Thus, the model is trained toward the objective of generating strings with the largest likelihood given input strings. The generation algorithm efficiently performs the top k candidates generation using top k pruning. To find the best k candidates pruning is guaranteed without enumerating all the possibilities. |
RELATED WORK
|
| There are several papers dealing with the information processing. But the major difference between our work and the existing work is that we focus on enhancement of both accuracy and efficiency of string transformation. Dreyer [7] also proposed a log linear model for string transformation, with features representing latent alignments between the input and output strings. Tejada [9] proposed an active learning method that can estimate the weights of transformation rules with limited user input. Arasu [8] proposed a method which can learn a set of transformation rules that explain most of the given examples. There are also methods for finding the top k candidates by using n-g rams [10], [11]. Wang and Zhai [14] mined contextual substitution patterns and tried to replace the words in the input query by using the patterns. Brill and Moore [5] developed a generative model including contextual substitution rules. Toutanova and Moore [12] further improved the model by adding pronunciation factors into the model. Duan and Hsu [13] also proposed a generative approach to spelling correction using a noisy channel model. |
Learning for String Transformation
|
| String transformation is about generating one string from another string, such as “TKDE” from “Transactions on Knowledge and Data Engineering”. Studies have been conducted on automated learning of a transformation model from data. Arasu et al. [8] proposed a method which can learn a set of transformation rules that explain most of the given examples. Increasing the coverage of the rule set was the primary focus. Tejada et al. [9] proposed an active learning method that can estimate the weights of transformation rules with limited user input. The types of the transformation rules are predefined such as stemming, prefix, suffix and acronym. Okazaki et al. [6] incorporated rules into an L1-regularized logistic regression model and utilized the model for string transformation. Dreyer et al. [7] also proposed a log linear model for string transformation, with features representing latent alignments between the input and output strings. Finite-state transducers are employed to generate the candidates. Efficiency is not their main consideration since it is used for offline application. Our model is different from Dreyer et al.’s model in several points. Particularly our model is designed for both accurate and efficient string transformation, with transformation rules as features and non-positive values as feature weights. |
| Okazaki et al.’s model is largely different from the model proposed in this paper, although both are discriminative models. Their model is defined as a logistic regression model (classification model) P(t j s), where s and t denote input string and output string respectively, and a feature represents a substitution rule fk(s; t) = { 1 rule rk can convert s to t 0 otherwise (1) Their model utilizes all the rules that can convert s to t and it is assumed only one rule can be applied each time. |
PROPOSED WORK
|
String Transformation Model
|
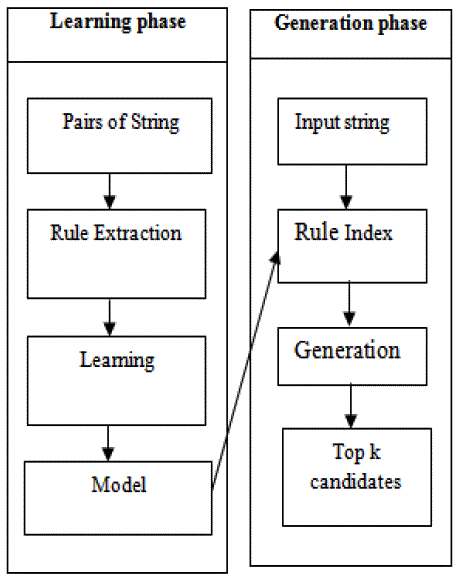
| The overview of our method is shown in Fig. 3. There are two processes, they are learning and generation. In the learning process, rules are first extracted from training pairs of string. Then the model of string transformation is constructed using the learning system, deals with rules and weights. In the generation process, given a new input string, produces the top k candidates of output string by referring to the model (rules and weights) stored in the rule index. |
| The model consists of rules and weights. A rule is formally represented as α → β which denotes an operation of replacing substring α in the input string with substring β, where α, β € { s|s = t, s = ^t, s = t$, or s = ^t$ } and t € Σ* is the set of possible strings over the alphabet, and ^ and $ are the start and end symbols |
Step 1: Edit-distance based alignment
|
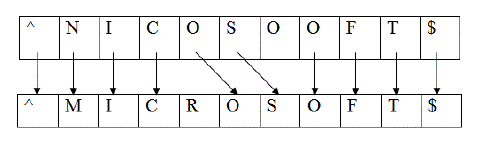 |
Step 2: Rules derived
|
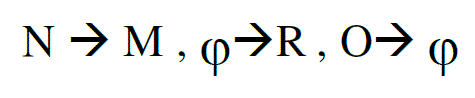 |
Step 3: Context expanded rules
|
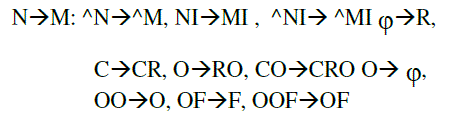 |
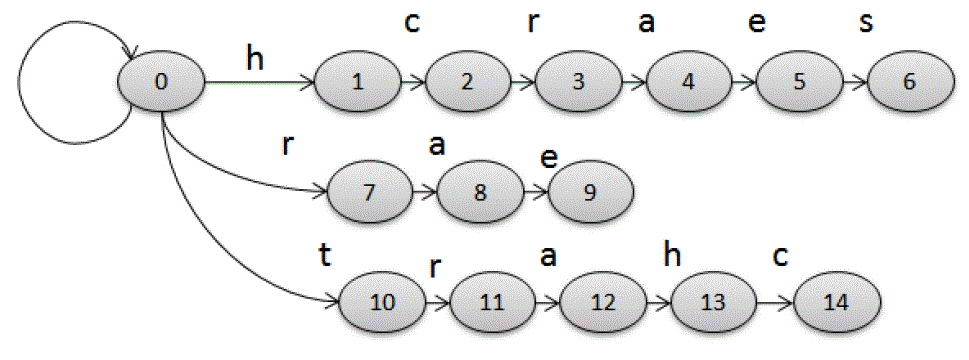
| Fig 4. Rule Extraction example |
| All the possible rules are derived from the training data based on string alignment. Fig. 4 shows derivation of characterlevel rules from character-level alignment. First we align the characters in the input string and the output string based on edit-distance, and then derives rules from the alignment. |
Log Linear Model
|
| A log-linear model consists of the following components: |
| • A set X of possible inputs. |
| • A set Y of possible labels. The set Y is assumed to be finite. |
| • A positive integer d specifies the number of features and parameters in the model. |
| • A function f : X * Y ? Rd that maps any (x, y) pair to a feature-vector f(x, y). |
| • A parameter vector v € Rd. For any x € X, y € Y, the model defines a conditional probability |
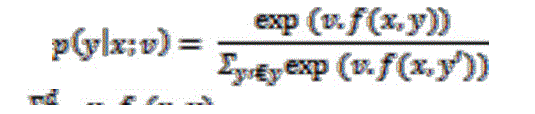 |
Here exp (x) = ex, and 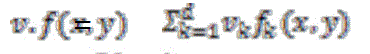 |
| is the inner product between f(x,y) and v. The term is intended to be read as “the probability of y conditioned on x, in the parameter values v”. |
| We now describe the components of the model in more detail, first focusing on the feature-vector definitions f(x,y) , then giving intuition behind the model form |
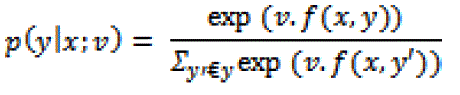 |
| The models can be represented by a set of expected frequencies that may or may not resemble the observed frequencies. The following model is referring to the traditional chi-square test where two variables, each with two levels (2 x 2 table), to be evaluated to see if an association exists between the variables. |
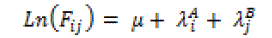 |
| Ln(Fij) = is the log, expected cell frequencies of the cases for cell ij in the contingency table. |
| μ = is the whole mean of the natural log of the expected frequencies |
| λ = terms each represent “effects” which the variables have on the cell frequencies |
| A and B = the variables |
| i and j = refer to the categories within the variables |
| Therefore: |
| = the main effect for variable A |
| = the main effect for variable B |
| = is the interaction effects for variables B and A |
| The above model is considered a Saturated Model because it includes all possible one way and two- way effects. The saturated model has the same amount of cells in the contingency table as it does effects as given, the expected cell frequencies will always exactly match the observed frequencies, with no degrees of freedom remaining. For example, in a 2 x 2 table there are four cells and in a saturated model involving two variables there are four effects, ?, , , , therefore the expected cell frequencies will exactly match the observed frequencies. In order to find a more parsimonious model that will isolate the effects best demonstrating the data patterns, must be sought as an a non-saturated model. This can be achieved by setting the parameters as zero to some of the effect parameters . For instance, if we set the effects parameter ?ij AB to zero (i.e. we assume that variable A has no effect on variable B and also B has no effect on variable A. we are left with the unsaturated model. |
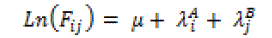 |
| This particular unsaturated model is titled as the Independence Model because it lacks an interaction effect parameter between A and B. This model holds that the variables are unassociated, implicity. Note that the independence model is analogous to the chi-square analysis and testing should be the hypothesis of independence. |
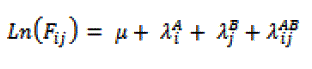 |
| Ln(Fij) = is the log, expected cell frequencies of the cases for cell ij in the contingency table. |
| μ= is the whole mean of the natural log of the expected frequencies |
| λ= terms each represent “effects” which the variables have on the cell frequencies |
| A and B = the variables |
| i and j = refer to the categories within the variables |
| Therefore: |
| = the main effect for variable A |
| = the main effect for variable B |
| = is the interaction effects for variables B and A |
| The above model is considered a Saturated Model because it includes all possible one way and two- way effects. The saturated model has the same amount of cells in the contingency table as it does effects as given, the expected cell frequencies will always exactly match the observed frequencies, with no degrees of freedom remaining. For example, in a 2 x 2 table there are four cells and in a saturated model involving two variables there are four effects, ?, , , , therefore the expected cell frequencies will exactly match the observed frequencies. In order to find a more parsimonious model that will isolate the effects best demonstrating the data patterns, must be sought as an a non-saturated model. This can be achieved by setting the parameters as zero to some of the effect parameters . For instance, if we set the effects parameter ?ij AB to zero (i.e. we assume that variable A has no effect on variable B and also B has no effect on variable A. we are left with the unsaturated model. |
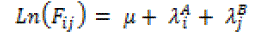 |
| This particular unsaturated model is titled as the Independence Model because it lacks an interaction effect parameter between A and B. This model holds that the variables are un associated, implicitly. Note that the independence model is analogous to the chi-square analysis and testing should be the hypothesis of independence. |
String Generation Algorithm
|
| Top k pruning algorithm is used to efficiently generate the optimal k output string. Aho–Corasick string matching algorithm is a string searching algorithms. It is otherwise known as dictionary-matching algorithm that locates the elements of a finite set of strings (the "dictionary") within an input text. Which matches all the patterns simultaneously and the complexity of the algorithm is linear in the length of the patterns plus the length of the searched text plus the number of output matches. The string generation problem amounts to that of finding the top k output strings given the input string. |
Algorithm1:(For Reference) Top k Pruning
|
| Input: Input string s, Rule index Ir, candidate key k |
| Output: top k output strings in stopk |
| 1. begin |
| 2. Find all rules applicable to s from Lr with Aho- Corasick algorithm |
| 3. minscore = -∞ |
| 4. Qpath=Stopk={} |
| 5. Add (1, ^, 0) into Qpath |
| 6. while Qpath is not empty do |
| 7. Pickup a path (pos,string,score) from Qpath with heuristics |
| 8. if score ≤ minscore then |
| 9. continue |
String Matching Algorithm
|
A) Knuth-Morris-Pratt Algorithm
|
| The Knuth-Morris-Pratt algorithm is based on finite automata but uses a simpler method of handling the situation of when the characters don’t match. In the Knuth-Morris-Pratt algorithm, we label the states with the symbol that should match at that point. We then only need two links from each state, one link for a successful match and the other link for a failure. The success link will take us to the next node in the chain, and the failure link will take us back to a previous node based on the word pattern. Which provide each success link of a Knuth-Morris-Pratt automata causes the “fetch” of a new character from the text. Failure links do not get a new character but reuse the last character that can be fetched. If we reach the final state, we know that we found the substring. |
B) Boyer-Moore Algorithm
|
| The Boyer-Moore algorithm is different from the previous two algorithms in that it matches the pattern from the right end instead of left . For example, in the following example, we first compare the y with the r and find a mismatch character. Because r doesn’t appear in the pattern at all, we know the pattern can be moved to the right a full four characters (the size of the pattern). We next compare the y with the h and find a mismatch. This time because the h does appear in the pattern, we have to move the pattern only two characters to the right so that the h characters line up and then we begin the match from the right side and find a complete match for the pattern. |
C. Commentz – Walter String Matching Algorithm
|
| Commentz-Walter algorithm is the combination of the Boyer- Moore technique with the Aho-Corasick algorithm,So this algorithm provide more accuracy and efficiency in string transformation. In pre- processing stage, it differs from Aho-Corasick algorithm, Commentz-Walter algorithm builds a converse state machine from the patterns to be matched. Each pattern to be matched and adds states to the machine starting from right side and going to the first character of the pattern, and combining the same node. In searching stage, Commentz-Walter algorithm Which uses the idea of BM algorithm. The length of matching window is the minimum pattern length. In matching window, Commentz-Walter that scans the characters of the pattern from right to left beginning with the rightmost one. In the case of a mismatch (or a complete match of the whole pattern) it uses a pre-computed shift table to shift the window to the right. |
PERFORMANCE ANALYSIS
|
| Next, we tested how to reduce the running time of our method changes according to three factors: |
| Dictionary size, maximum number of applicable rules in a transformation and rule set size. |
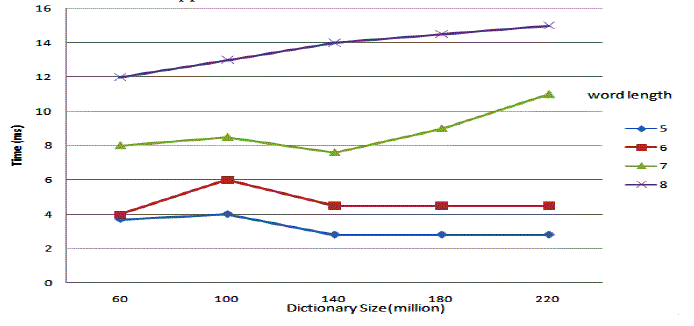
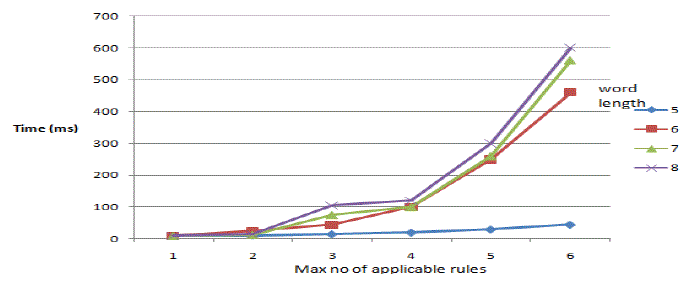
| In Fig.7, with increasing dictionary size, the running time is almost stable, which means our method performs well when the dictionary is large. In Fig. 8, with increasing maximum number of applicable rules in a transformation, the running time increases first and then stabilizes, especially when the word is long. |
| In Fig. 9, the running time keeps growing when the length of words gets longer. However, the running time is still very small, which can meet the requirement of an online application. From all the figures, we can conclude that our pruning strategy is very effective and our method is always efficient especially when the length of query is short. |
CONCLUSION AND FUTURE WORK
|
| Thus our work reduces the problem with information processing by making use of a new statistical learning approach to string transformation. This method is novel and unique in its model, learning algorithm, string generation algorithm and commentz walter algorithm. The commentz walter algorithm provides more accuracy and efficiency in Specific applications such as spelling error correction and query reformulation in web queries were addressed with this method. Experimental results on two large data sets show that our method improves upon the baselines in terms of accuracy and efficiency in string transformation. Our method is particularly more useful when the problem occurs on a large scale datasets. Experimental results on two large data sets and Microsoft Speller Challenge show that our method improves upon the baselines in terms of accuracy and efficiency. Our method is particularly useful when the -problem occurs on a large scale. |
Figures at a glance
|
 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
|
| |
References
|
- M. Li, Y. Zhang, M. Zhu, and M. Zhou, “Exploring distributional similarity based models for query spelling correction,” in Proceedings of the 21st International Conference on Computational Linguistics and the 44th annual meeting of the Association for Computational Linguistics, ser. ACL ’06. Morristown, NJ, USA:
- Association for Computational Linguistics, 2006, pp. 1025–1032.
- [A. R. Golding and D. Roth, “A winnow-based approach to context-sensitive spelling correction,” Mach. Learn., vol. 34, pp. 107–130, February 1999.
- J. Guo, G. Xu, H. Li, and X. Cheng, “A unified and discriminative model for query refinement,” in Proceedings of the 31st annual international ACM SIGIR conference on Research and development in information retrieval, ser. SIGIR ’08. New York, NY, USA: ACM, 2008, pp. 379–386.
- Behm, S. Ji, C. Li, and J. Lu, “Space-constrained gram-based indexing for efficient approximate string search,” in Proceedings of the 2009 IEEE International Conference on Data Engineering, ser. ICDE ’09. Washington, DC, USA: IEEE Computer Society, 2009, pp. 604–615.
- E. Brill and R. C. Moore, “An improved error model for noisy channel spelling correction,” in Proceedings of the 38th Annual Meeting on Association for Computational Linguistics, ser. ACL ’00. Morristown, NJ, USA: Association for Computational Linguistics, 2000, pp. 286–293.
- N. Okazaki, Y. Tsuruoka, S. Ananiadou, and J. Tsujii, “A discriminative candidate generator for string transformations,” in Proceedings of the Conference on Empirical Methods in Natural Language Processing, ser. EMNLP ’08. Morristown, NJ, USA: Association for Computational Linguistics, 2008, pp. 447–456.
- M. Dreyer, J. R. Smith, and J. Eisner, “Latent-variable modeling of string transductions with finite-state methods,” in Proceedings of the Conference on Empirical Methods in Natural Language Processing, ser. EMNLP ’08. Stroudsburg, PA, USA: Association for Computational Linguistics, 2008, pp. 1080–1089.
- Arasu, S. Chaudhuri, and R. Kaushik, “Learning string transformations from examples,” Proc. VLDB Endow., vol. 2, pp. 514– 525, August 2009.
- S. Tejada, C. A. Knoblock, and S. Minton, “Learning domain independent string transformation weights for high accuracy object identification,” in Proceedings of the eighth ACM SIGKDD international conference on Knowledge discovery and data mining, ser. KDD ’02. New York, NY, USA: ACM, 2002, pp. 350–359.
- M. Hadjieleftheriou and C. Li, “Efficient approximate search on string collections,” Proc. VLDB Endow., vol. 2, pp. 1660–1661, August 2009.
- C. Li, B. Wang, and X. Yang, “Vgram: improving performance of approximate queries on string collections using variable-length grams,” in Proceedings of the 33rd international conference on Very large data bases, ser. VLDB ’07. VLDB Endowment, 2007, pp. 303–314.
- X. Yang, B. Wang, and C. Li, “Cost-based variable-length-gram selection for string collections to support approximate queries efficiently,” in Proceedings of the 2008 ACM SIGMOD international conference on Management of data, ser. SIGMOD ’08. New York, NY, USA: ACM, 2008, pp. 353–364.
- C. Li, J. Lu, and Y. Lu, “Efficient merging and filtering algorithms for approximate string searches,” in Proceedings of the 2008 IEEE 24th International Conference on Data Engineering, ser. ICDE ’08. Washington, DC, USA: IEEE Computer Society, 2008, pp. 257–266.
- S. Ji, G. Li, C. Li, and J. Feng, “Efficient interactive fuzzy keyword search,” in Proceedings of the 18th international conference on World wide web, ser. WWW ’09. New York, NY, USA: ACM, 2009, pp. 371–380.
- R. Vernica and C. Li, “Efficient top-k algorithms for fuzzy search in string collections,” in Proceedings of the First International Workshop on Keyword Search on Structured Data, ser. KEYS ’09. New York, NY, USA: ACM, 2009, pp. 9–14.
|