International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Low Pass FIR Filter Design and Analysis Using Hamming, Blackman and Kaiser Windows

Suhaib Ahmed1, Mudasir Bashir2, Ashish Suri3
  1. M.Tech Student, School of Electronics and Communication Engineering, SMVD University, Katra, India
  2. M.Tech Student, School of Electronics and Communication Engineering, SMVD University, Katra, India
  3. Assistant Professor, School of Electronics and Communication Engineering, SMVD University, Katra, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

The recent advancements in the field of communication systems are challenging the engineers to design digital equipments as ubiquitous in various areas like power systems, audio applications, image processing, etc. Hence digital filters have to be improvised time-to-time to cope-up with different characteristics featured by the system while taking into consideration the accuracy, speed and stability issues arising due to growing variety and complexity of the conditions faced along the operation of the system. In this paper, low pass finite impulse response (FIR) filters are designed using the Hamming, Blackman and Kaiser Windows and their corresponding magnitude and phase responses are analysed at a given filter order and its cut-off frequency. It is shown that the degree of flatness of the transition band varies with order of the filter.

Keywords
Low Pass FIR filter; Hamming Window; Blackman Window; Kaiser Window

I. INTRODUCTION
Digital Signal Processing affords greater flexibility, higher performance (in terms of attenuation and selectivity), better time and environment stability and lower equipment production costs than traditional analog techniques. Digital filters are a very important part of DSP. In fact, their extraordinary performance is one of the key reasons that DSP has become so popular. A filter is essentially a network that selectively changes the wave shape of a signal in a desired manner [1][2]. The objective of filtering is to achieve signal separation and signal restoration. Signal separation is needed when a signal has been contaminated with interference, noise, or other signals and Signal restoration is used when a signal has been destroyed in some way. For example, an audio recording made with some poor device may be filtered to better represent the sound as it actually occurred [3].
A discrete-time, discrete-amplitude convolver can be considered as a digital filter. Digital filters differ from conventional analog filters by their use of finite precision to represent signals and coefficients and finite precision arithmetic to compute the filter response. According to Fourier transform the linear convolution of two sequences is equivalent to multiplication of two corresponding spectral sequences in the frequency domain [6]. The multiplication of signal spectrum by frequency domain impulse response of the filter, or in time-domain, convolution of input signal with filter’s impulse response, is the basic method of implementing a digital filter. Digital filters are classified either as finite duration unit pulse response (FIR) filters or Infinite duration unit pulse response (IIR) filters, depending on the form of the unit pulse response of the system. FIR filters are filters having a transfer function of a polynomial in z- and are an all-zero filter in the sense that the zeroes in the z-plane determine the frequency response magnitude characteristic [1][2]. The z transform of N-point FIR filter is given by
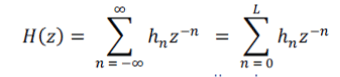Where L = N – 1.
Thus, the transfer function of every length N = L + 1 FIR filter is an Lth order polynomial in z-1. FIR filters are employed in filtering problems where linear phase characteristics within the pass band of the filter are required. To obtain an FIR filter which approximates the original frequency response, the Fourier series expansion of the system must be truncated, but the direct truncation of the series leads to Gibbs phenomenon, i.e., a fixed percentage overshoot and ripple before and after an approximated discontinuity, which in undesired. In order to avoid this, a time-limited weighting function called window is used [7]. In this paper, the spectral responses of Hamming, Blackman and Kaiser Windows are analyzed for odd filter order N. The general equation of frequency response H(ω) for odd number of N [4] is given by
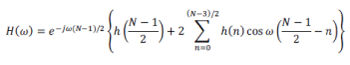Now comparing H(��) with the polar representation of H(��), the magnitude is
H(��) = |H1(��)|
Where H1(ω) is a real quantity given by
In this paper, the magnitude of H(��) has been analyzed for different design techniques. The unit sample response hd(n) of the linear ideal low pass filter is determined from the Inverse Fourier Transform of the frequency response of the Ideal Low Pass Digital Filter [4] and is given by
Where �� = (N – 1) / 2.
In order to develop stable and realizable transfer function, the infinite duration impulse response is converted to a finite duration impulse response by truncating the impulse response to a finite number of terms. This can be achieved using various window design techniques as presented in the paper.

II. ANALYTICAL DESIGN OF LOW PASS FIR FILTERUSING HAMMING WINDOW
The Hamming Window is one of the most popular and most commonly used windows. A filter designed with the Hamming window has minimum stop band attenuation of 53dB, which is sufficient for most implementations of digital filters. The Hamming Window [1],[2] is defined by
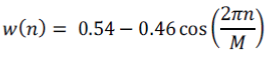for 0 ≤ n ≤ M
The values of filter impulse response coefficients, h(n) for Blackman window at ��S = 0.4 rad/s and filter order 61, are following:

III. ANALYTICAL DESIGN OF LOW PASS FIR FILTERUSING BLACKMAN WINDOW
The Blackman Window has relatively high attenuation, which makes this window very convenient for almost all applications. The minimum stopband attenuation of a filter designed with this window amounts to 75dB. The Blackman Window [1],[2] is defined by
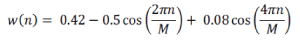for 0 ≤ n ≤ M
The values of filter impulse response coefficients, h(n) for Blackman window at ��S = 0.4 rad/s and filter order 61, are following:
The corresponding frequency response and phase response of the Low Pass Filter are shown in Fig. 3 and Fig. 4.

IV. ANALYTICAL DESIGN OF LOW PASS FIR FILTERUSING KAISER WINDOW
A desirable property of the window function is that the function is of finite duration in the time domain and that the Fourier transform has maximum energy in the main lobe or a given peak side lobe amplitude [2]. The prolate spheroidal functions [5] have this desirable property; however these functions are complicated and difficult to compute. A simple approximation to these functions has been developed by Kaiser in terms of zeroth order modified Bessel functions of the first kind. In a Kaiser window, the side lobe level can be controlled with respect to the main lobe peak by varying a parameter, β [2]. The width of main lobe can be varied by adjusting the length of the filter. The Kaiser Window function is given by
The frequency response and phase response of the Low Pass Filter using Kaiser Window are shown in Fig. 5 and Fig. 6 respectively for filter order 61 and normalised cut-off frequency ��S = 0.4 rad/s.

V. SIMULATION AND PERFORMANCE EVALUATION
The magnitude responses and phase responses of different design techniques for Low Pass FIR Filter with normalised cut-off frequency ��S = 0.4 rad/s and filter order = 61, are illustrated in Fig. 7, Fig. 8 and Fig. 9.
Low Pass FIR Filter using Kaiser Window shows superior transition from pass band to stop band at the cut-off frequency ��S = 0.4 rad/s but as can be seen from the frequency response in Fig. 7, pass band has ripples or oscillations due to side lobes of the window function and there are relatively large oscillations or ripples near the cut-off frequency.. The simulation was done for β=0.5. When β=0, Kaiser Window will act as a Rectangular window and when β=5.4414, Kaiser Window acts as a Hamming Window. Increasing β further gives further reduced stop-band ripples but with a reduced cut-off sharpness. Hence ripple reduction is at the expense of the poor transition from pass band to stop band at the cut-off frequency. The Blackman Window achieves much better stop band attenuation but as can be seen from Fig. 7, the Blackman Window frequency response shows poor performance in the transition band as compared to other windows.
The normalized cut-off frequency ��S was changed from 0.4 rad/s to 0.6 rad/s and the simulation was repeated again. As can be seen from Fig. 10, there is no change in the stop band attenuation, pass band and stop band ripples for all windows.
Next, the order of the filter N is increased from 61 to 201 and simulation is done. As can be seen from Fig. 11, as the filter order is increased the performance of all windows increases in the transition band and their frequency response approximates the ideal Low Pass Filter response. The main disadvantage of the windows is that one must compute Bessel functions to compute window coefficients [8].

VI. CONCLUSION
The design of Low Pass FIR Filter using Kaiser Window is suitable if the transition band is of utmost importance but if we consider other parameters then, Blackman Window provides better stop band attenuation. In general, Hamming Window can be considered as a stable window as it provides with good attenuation and a better transition from pass band to stop band at cut-off frequency than Blackman and Kaiser Windows.
 

Tables at a glance
Table icon Table icon Table icon
Table 1 Table 2 Table 3
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4
Figure 1 Figure 2 Figure 3 Figure 4
Figure 1 Figure 2 Figure 3 Figure 4
Figure 5 Figure 6 Figure 7 Figure 8
Figure 1 Figure 2 Figure 3
Figure 9 Figure 10 Figure 11
 

References