Mathematical Model of High-Voltage Brushless Synchronous Generator

Abstract

The mathematical models of salient-pole high-voltage synchronous generator with brushless excitation system in d, q axis are presented

Keywords

Mathematical model, brushless synchronous generator, brushless excitation system.

Introduction

In some modern unified high-voltage automated electro energetic ship systems (UHAEES), we largely use brushless synchronous generators with high-voltage (6.6 kv) and diesel control. In such a synchronous generator (SG) as excitation system we use a synchronous machine with three phase windings in rotor and excitation winding in stator. The voltage at three-phase windings is converted with rotating diode converter and is supplied to excitation winding of SG.

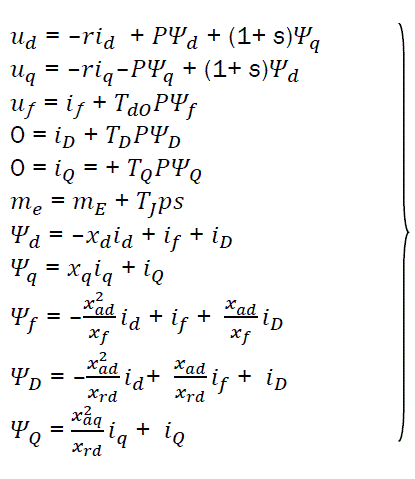eq1

Where u_d, u_q – stator loop voltages;

i_d, i_q – stator winding currents;

Ψ_d, Ψ_q – glowing flux of stator winding

i_f, Ψ_f - current and flux of excitation winding

iD, iQ – currents in damper windings;

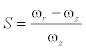- Slip of rotor related to synchronous speed;

m_E= Ψ_diq + Ψ_qid – electromagnetic torque of machine;

P = d/dt_b - differential symbol with argument tb

r – active resistance of stator winding;

T_do, T_D, T_Q – time constants of excitation circuit and damper windings;

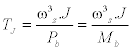-Motor Inertia Constant

x_d,x_q - synchronous reactivities of stator;

x_ad, x_aq – reactivities of stator self-induction

x_rd, x_rq, total reactivities of damper windings;

For a voltage regulation, we use constant voltage electronic impulse regulator which transforms the constant voltage of supply source into a regulated voltage of excitation winding for the synchronous exciter. In such transformations, we use power semiconductors controlled elements IGBT – transistors, while their regulation is done through time-impulse voltage modulation of source supply.

Mathematical model of SG through d and q axesin per units system can be represented with the equation system [1]:

Physical Units Representation

For transformation from per unit representation to physical units, we multiply by basic values. For stator circuit, we use the following basic values: amplitudes of nominal stator voltage and current;

Ψ_b= U_b/ω_b-flux

Where ω_b=ω_s=2πƒ_b-Synchronous angular rotor speed (with ƒ_b = 50Hz, ω_s = 314.16 rad/sec;

Z_b =U_b/I_b – resistance;

- total power;

-rotating torque;

For winding excitation of SG, we use the following basic values:

For a longitudinal damper loop:

For transversal damper loop:

In equations (eq1) we considered all significant electromagnetic and electromechanical processes in the synchronous machine and in damper winding. Depending on specific particularities of the problem presented, (eq1) can be considerably simplified in their particular part without any great loss to the solution expected.

Concerning the equations, for all the means of automatization of SG, they should be transformed such that, input and output variable currents and voltages could represent corresponding vectors in d and q axes respectively in per units system.

Proposed Model

Getting to the mathematical model, describing brushless exciters in rotating coordinates, it is important to note that rotating axes of the machine are attached to the stator and not to the rotor in usual models. Since the coordinate axes of the exciters are not different from the axis of SG, we introduce for them other representations d1, q1. Therefore, the equations of synchronous exciters in per-units form are as follows:

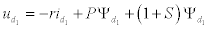
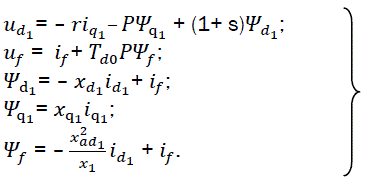eq2

u_d1, u_q1, u_f, i_d1, i_q1,i_f, Ψ_d1, Ψ_q1, Ψ_f – voltages, currents and flows through longitudinal and transversal axis of armature and winding for exciter respectively;

P – differential symbol;

s – rotor slip of the machine;

T_d0 – time constant of exciter circuit;

r, x_d1, x_q1, x_f – winding active and reactive resistances;

x_ad1 – reactivity of armature self-induction along longitudinal axis;

In approximate research related to transient processes in synchronous machines, equations can be simplified by excluding transformers emf in stator loops. If we simultaneously exclude pΨ_d1, pΨ_q1 and sΨ_d1, sΨ_q1 errors are each other compensated considerably. Further simplification is done by neglecting the active resistance of armature (r =0).

In that case exciter equations will be much simple:

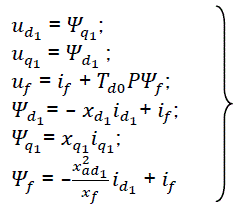eq3

We should also consider the link between exciter armature winding and exciter winding of the machine through rotating converter.

For that purpose, we can replace real load by a certain equivalent resistance RE [2,3,4,5].

Thus,

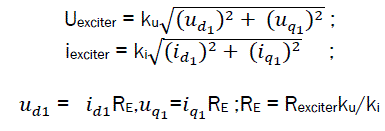eq4

Where, k_u and k_i depend on the structure of rotating converter and on parameters of machine excitation windings.

Conclusion

The proposed model of brushless synchronous generator can be used in computer modeling of UHAEES for perspective ships.

References

1. Baranov AP. Modelling of ship electrical equipment andmeans of automation: university manual/ A.P. Baranov, M.M. Rayimov. –SPG.:ELMOR, 1997. -232p. (in Russian).
2. BOUT DA. Contactless electrical machines/ D. A. Bout – M.: High school, 1990 – 417p (in Russian).
3. Colbia-Vega A, de Léon-Morales J, Fridman L, Salas-Péna O, & Mata-Jiménez MT. Robust excitation controldesign using sliding-mode technique formultimachinepowersystems. Electric Power Systems Res. 2008;78:1627–1634.
4. Ohtsuka K, Taniguichi T, Sato T, Yokokawa S, & Ueki Y. A H∞ optimal theory based generator control system. IEEE Transactions on Power Systems. 1992;7(1):108–113.
5. Park JW, Harley RG, &Venayagamoorthy GK. Adaptive-critic-based optimal neurocontrol for synchronous generators in a power system using MLP/RBF neural networks. IEEE Transactions on Industry Applications. 2003;39(5):1529–1540.