Method for Verifying the Rationality of Radar Data Based on Single Optical Theodolite

Abstract

The Pulse radar is one of the pillar equipment for aircraft navigation and control. Due to changes in the target state or environment, radar data may seriously deviate from the true situation of the target. When using radar data for navigation control, rationality check must be carried out to ensure that the radar data is normal. In order to solve the problem that existing algorithms need multiple theodolite data fusion to solve the target position coordinates to check the rationality of radar measurement data, a series of algorithms based on the angle measurement data of a single optical theodolite is proposed to realize the rationality check of pulse radar. The main feature of this paper is to use the two-dimensional data (azimuth angle and pitch angle of target) of theodolite to check the rationality of the three-dimensional data (range, azimuth and pitch angle of target in radar coordinate system) of radar. This method established in this paper effectively breaks through the limitation that it is necessary to use two or more theodolites to calibrate or verify the quality of pulse radar tracking data in the process of carrying out measurement and control tasks in the current engineering field, which is of great engineering value. This method proposed in this paper can be used to identify abnormal data and repair outliers in the navigation and control process of aircraft and moving objects, so as to avoid navigation errors and control deviations caused by abnormal data and outliers. The simulation results show that this method can be used with an accuracy rate of over 95% when the radar ranging data is normal but the quality of the angle measurement data is unknown, or when the radar angle measurement data is normal but the quality of the ranging data is unknown.

Keywords

Theodolite; Radar; Rationality check; Outliers

Introduction

Theodolite and radar are important tracking and measuring devices in the process of aircraft measurement and control. The tracking measurement data of theodolite, radar and other equipment are important basis for calculating the trajectory or orbit of the aircraft, and plays an important role in the safety control of the aircraft and the error analysis of the guidance system [1]. How to accurately determine the quality and accuracy of measurement data is the main research topic in the field of aircraft navigation and control.

Since the optical theodolite can only measure the pitch and azimuth angle of the output target relative to the theodolite, two or more theodolites are usually used to measure data in engineering practice, the target aircraft position is calculated by K-formula, L-formula or the least squared method [2-4], then the radial distance, azimuth angle and pitch angle relative to the pulse radar are inversely solved, comparing and analysing measurement errors of pulse radar to realize analysis and evaluation of tracking accuracy and data rationality of pulse radar [5]. Although the intersection positioning accuracy of multiple theodolites is high, the field of view is small and the operating distance is limited due to the limitation of the check site [6].

In the reliability evaluation of measurement and control networks, if a single optical theodolite can be used to verify or verify the quality of pulse radar data, it can effectively relax the limitation that classical methods require "two or more optical theodolites" to complete, and has very important engineering value. For this idea, this article explores and establishes a method for verifying the rationality of radar data using single theodolite measurement data. Specifically, this paper establishes radar data verification methods for three different scenarios: Case 1 is that the radar ranging data is known to be reliable, but the rationality of the radar angle data needs to be checked; Case 2 is that the radar angle measurement data is known to be normal, but the rationality of the ranging data needs to be checked; and Case 3 is that the quality of radar measurement data (ranging and angle measurement) is unknown and requires a rationality check.

Materials and Methods

Reasonability check of radar ranging in case 1

The purpose of the data rationality check is to determine whether the data is normal and reasonable and to discover abnormal data or outliers that may be implied in it. The function of reasonability check of pulse radar measurement data is to ensure that the radar measurement data used for trajectory calculation is accurate and reliable, and to avoid the influence of outliers of pulse radar measurement data on the accuracy and reliability of trajectory calculation results [5].

For the pulse radar measurement data, the distance (R_L) and angle (A_L, E_L) belong to different measurement channels, and the measurement mechanism is also different, generally, the distance and angle (A_L,E_L) may not present outlier at the same time during aircraft tracking. This section considers the rationality check of pulse radar ranging data in case 1.

Angle conversion algorithm in case 1: Assuming that an optical theodolite and a pulse radar track an aircraft synchronously (Figure 1). The azimuth and pitch angle(A_G,E_G) of the aircraft relative to the optical theodolite station coordinate system, and the radial distance and angle (R_L,A_L,E_L)relative to the pulse radar station coordinate system are obtained respectively.

Since the optical theodolite does not have the function of measuring distance, it cannot be used to verify and calibrate pulse radar measurement data directly through coordinate conversion. For this reason, this section tries to establish a set of coordinate transformation algorithms: The method of calculating the estimated angle data of target in the coordinate system of radar station based on theodolite angle measurement data.

Whether it is theodolite or pulse radar, the measurement data is relative to the coordinate system of the respective measuring station. The so-called station coordinate system refers to the three-dimensional coordinate system with the rotation center of the station equipment as the origin, the Y-axis pointing to the zenith, and the X-axis pointing to the geodetic north. In the process of engineering experiments, the geodetic measurement (geodetic longitude and latitude, geodetic elevation and vertical deviation) of the station can be used to establish the relationship between the origin coordinate and the rotation transformation of the coordinate system under the geocentric rectangular coordinate system (converted into a coordinate system parallel to the geocentric rectangular coordinate system) [7-9], and then the coordinates and rotation matrix of the radar station origin(O_L) in the rectangular coordinate system of the theodolite measuring station can be determined, and the coordinates and rotation matrix of the theodolite origin (O_G) in the rectangular coordinate system of the radar measuring station can be determined.

Record the coordinates of the theodolite rotation centre OG in the pulse radar station coordinate system as (X'_OG,Y'_OG,Z'_OG)the rotation matrix between the coordinate systems of the two measuring stations is Ω. Then from the theodolite measurement data, the position coordinates of the aircraft M in the pulse radar station coordinate system can be known as formula (1).

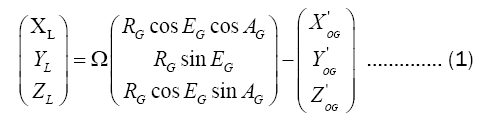
It is not difficult to derive from this, based on the optical theodolite measurement data, the radial distance R_R, azimuth angle A_R, and pitch angle E_R of the target M in the pulse radar station coordinate system can be expressed as formula (2).

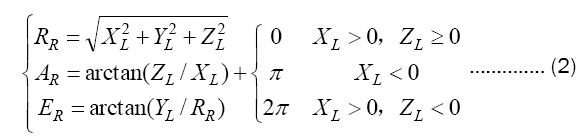
Since the radial distance between the optical theodolite and the aircraft is unknown, therefore, in order to calibrate and detect pulsed radar measurement data using formula (2), an estimated value of R_G must be given in advance.

Estimation of distance R_G in case 1: From Figure 1, it can be seen that the angle data measured by the theodolite determines that it is a ray, and the trajectory of the point with the distance of R_L from the rotation center of the pulse radar (OL) is a sphere. The origin coordinate of theodolite is (X'_OG,Y'_OG,Z'_OG)the coordinate of the rotating center of the pulse radar in the coordinate system of the optical theodolite measuring station is (X'_OL,Y'_OL,Z'_OL), radar ranging (R_L) is R_T under the coordinate system of theodolite measuring station and then the trajectory equations of the above ray and sphere in the coordinate system of the theodolite measuring station are given in formula 3.

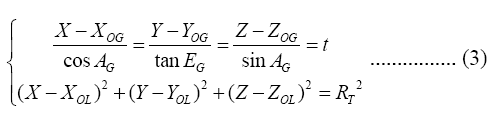
Under the coordinate system of the theodolite measuring station, the origin coordinate of the theodolite can be considered

X_OG,=Y_OG=,Z_OG=0 combining formula (3) can get quadratic equation of one unknown.

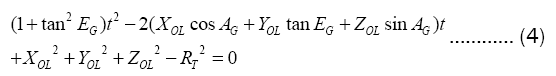
The ray and the ball may not intersect, intersect at two points, or tangent to one point (Figure 2), combined with Figure 2, it is not difficult to give the estimation algorithm of R_G in three different cases: disjoint, intersection and tangent.

Estimation of RG when tangent: Solving quadratic equation of one unknown (4), when t has only one solution, the ray is tangent to the ball, at this time, the tangent point can be considered as the location of target M.

Substituting t into the ray trajectory equation in (3), it can get formula (5).

The estimator of R_G is formula (6).

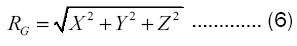
Estimation of R_G when intersection: Solving the equation (4), we obtain two solutions T1 and T2, which are the two points where the ray intersects the sphere. The middle point of the line connecting the two intersection points is the position of target M.

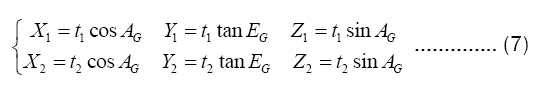
Then the estimator of R_G is formula (8).

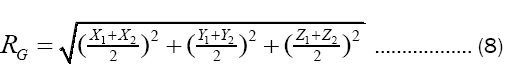
Estimation of RG when disjoint: Solving the equation (4), if t has no solution, then the ray does not intersect the sphere, at this time, it can be considered that the point on the ball at the shortest distance between the ray and the sphere is the location of the target M. The calculation process is as follows:

Assuming that the vertical point from (X_OL,Y_OL,Z_OL),to ray is coordinates(X_C,Y_C,Z_C) substituting into the ray trajectory equation of formula (3), it can get formula (9).

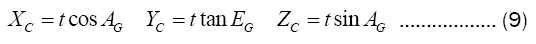
The vertical vector 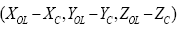is orthogonal to the ray vector 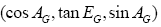so we get:

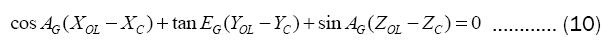
Substituting the formula (9) into the formula (10) to get the formula (11).

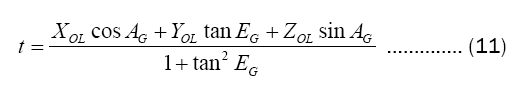
The distance d between the point and the ray is equal to.

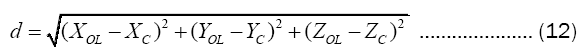
In formula (12), (X_C,Y_C,Z_C) can be substituted and eliminated by formula (9) and formula (11). Therefore, the estimator of R_G can be obtained.

Rationality check of radar data based on residuals: Comparison analysis is one of the common methods to analyze the quality of measurement data, and has a wide range of applications in the field of aircraft measurement and control [10].

Usually, in the process of radar measurement data analysis and processing, the cross comparison technology of different source data can effectively judge the quality of measurement data and identify abnormal data.

In this section, the measurement data of the pulse radar is checked based on the Angle measurement data and range estimation value of a single optical theodolite. The specific methods are as follows:

1) Assuming that the theodolite angle measurement data is reliable, optimal estimation of the Radial distance (R_G) between the theodolite and the target by the calculation methods in section estimation of distance RG in case 1, substitute the theodolite measurement data (R_G.A_G,E_G) into formula (2), calculate the Radial distance(R_R), Azimuth angle (A_R), and Pitch angle (E_R) of the target M in the pulse radar station coordinate system based on the optical theodolite measurement data.

2) For moving target, whether it is the measured data (R_L,A_L,E_L) from radar or the (R_R,A_R,E_R) calculated from the theodolite data (A(t_i),E(t_i)) the residuals are as follows:

In formula (14),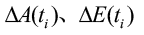 is the difference in measurement metadata between two measurement stations.

3) The detection threshold is determined based on the comparison residuals. The threshold constants include the azimuth threshold constant and the pitch angle threshold constant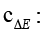

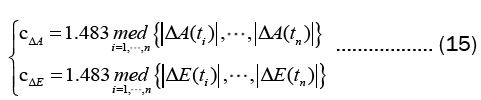
Using 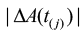to represent the j-th numerical value of data 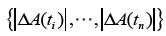sorted from the smallest to the largest, the sample median operator is as follows

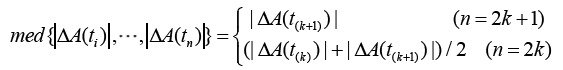
Taking azimuth data as an example, an outlier detection method is constructed: a) if 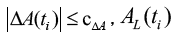is judged to be normal; b) if 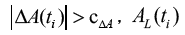is judged to be outlier.

The abnormal value detection method of pitch angle data and azimuth angle data is the same.

Reasonability check of radar angle in case 2

Distance estimation in case 2: This section considers the estimation algorithm of the distance (R_G) between the target and the theodolite when the radar angle measurement data (A_L,E_L) is not outliers. Setting the coordinate of radar angular data in theodolite station coordinate system as(A_T,E_T), the rotation matrix between coordinate systems of two stations is Ω, according to the radar angle data, the direction cosine of the aircraft M in the theodolite measuring station coordinate system is formula (16).

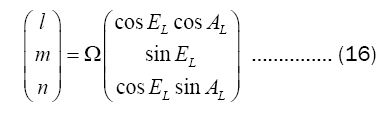
The coordinate of the radar angle measurement data in the theodolite measurement station coordinate system is as follows.

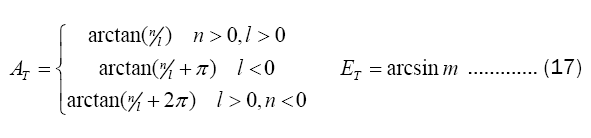
Based on radar angle measurement data (A_T,A_E)and theodolite angle measurement data(A_G,E_G) the optimal estimation of point M(XYZ) coordinate is calculated using the shortest distance and fused positioning method [11,12].

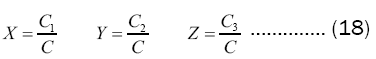
Where

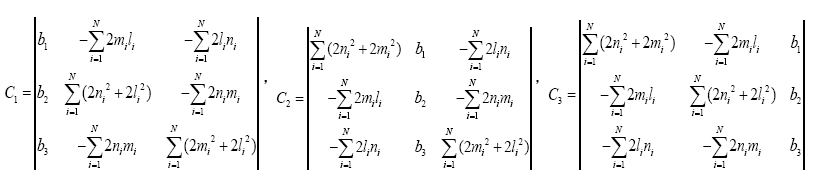
Where N is the number of measuring devices (N=2).

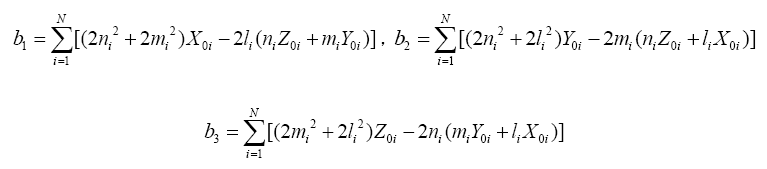
Where 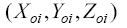is the location coordinate of the radar and theodolite in the coordinate system of the theodolite station Therefore, the estimated distance (RG) between the target and the theodolite is formula (19).

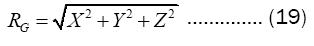
Rationality check of radar angle based on residuals: Assuming that the theodolite angle measurement data is reliable, optimal estimation of the Radial distance (R_G) between the theodolite and the target by the calculation methods in section distance estimation in case 2, we substitute the theodolite measurement data (R_G,A_G,E_G) into the formula (2), calculate the Radial distance (R_R), Azimuth angle (A_R), and Pitch angle (E_R) of the target M in the pulse radar station coordinate system based on the optical theodolite measurement data.

For moving target, whether it is the measured data (R_L,A_L,E_L) of the compared radar or the (R_R,A_R,E_R) calculated back from the theodolite measurement data, it usually changes with time, therefore, the measurement data at time t_i is R(t)_i, and the alignment residual sequence is as follows:

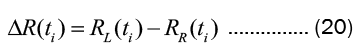
The threshold constant was determined based on the contrast residual:

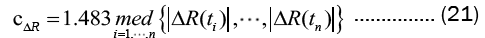
Where the sample median operator

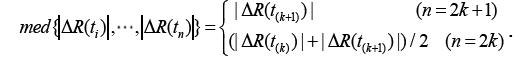
Where the 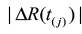represents the j-th numerical value of data sorted from the smallest to the largest.

The method of outlier detection of ranging data is constructed: a) if 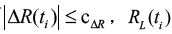is judged to be normal; b) if 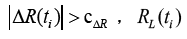is judged to be outlier.

Rationality check of radar data in case 3

Assuming the theodolite angle measurement data is reliable, in the case of unknown radar measurement data quality, the distance R_L and angle (A_L,E_L) of pulse radar measurement data are calculated inversely as the angle (A_F,E_F) of the aircraft relative to the theodolite. The conversion method is as follows: Remember that the coordinates of the rotating center OL of pulse radar in the theodolite station coordinate system is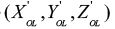, the rotation matrix between the two station coordinate system for Ω, according to formula (1), it can be derived that the position coordinate of aircraft M under the coordinate system of theodolite station is 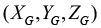according to the measured data of pulse radar. Then, according to formula (2), the azimuth angle A_F and pitch angle E_F in the coordinate system of theodolite station can be obtained. Then,

the angle data (A_F,E_F)obtained by inverse calculation is compared with the original angle data (A_G,E_G),of theodolite by comparing the residual analysis method. The specific algorithm is as follows:

1) For moving target, whether it is the measured data (A_G,E_G)of the compared theodolite or the (A_F,E_F) calculated back from the pulse radar measurement data, it usually changes with time, therefore, the measurement data at time t_i is 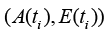and construct the alignment residual sequence of formula (14).

2) Based on comparing the residual determine the detection threshold of such as formula (15), the threshold constant including azimuth threshold constant , pitching angle threshold constant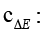

3) Taking azimuth data as an example, an outlier detection method is constructed: a) if 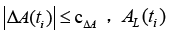is judged to be normal; b) if 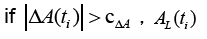is judged to be outlier.

When 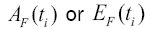is abnormal, the measured data of pulse radar is abnormal. When are normal values, the measured data of pulse radar are normal values.

Results and Discussion

Simulation calculation

In order to verify the effectiveness of the algorithm for checking the rationality of pulse radar measurement based on the angle data of a single optical theodolite, this section uses the nominal trajectory data in flight inspection and the measurement data of a single radar as the simulation data, with a sampling interval of 0.1 s, and a total of 1859 points. Since the standard trajectory data are 3-dimensional time series, it can be calculated as the azimuth and elevation angle of the target relative to the coordinate system of a single optical Theodolite measurement station (Figure 3). The curve of radar measurement data over time are shown in Figure 4.

Angle rationality check when ranging is normal: In order to simulate normal ranging data and abnormal angle measurement data from the pulse radar, As shown in Figure 4, the azimuth (AL) and elevation (EL) are randomly added with 2% gross error, there are 37 outliers in 1859 data, and the angle measurement data plots including outliers are obtained, as shown in Figure 5.

The data rationality test method based on comparative residuals in reasonability check of radar ranging in case 1 is used to detect the abnormal data in the radar angle measurement data. The results are shown in Figure 6. The data with red marks in the figure are the identified outliers.

Ranging rationality check when angles are normal: In order to simulate the occasional losses of radar data, a total of 2% grosses are added to the distance (R_L) data shown in Figure 4 to obtain the pulse radar distance data with abnormal points shown in Figure 7. The data rationality check method based on comparative residuals in reasonability check of radar angle in case 2 is used to detect the measured data of the pulse radar. The simulation results are shown in Figure 8. The data of the blue marked points in the figure are the identified outliers.

Rationality check of the unknown radar data: In scenario 3, 2% grosses are added to the ranging data (RL), azimuth angle (AL) and pitch angle (EL) shown in Figure 4 to obtain the measurement data plots including outliers, as shown in Figure 9.

Using the rationality check method given rationality check of radar data in case 3 to discriminate the measured data of pulse radar. The simulation results are shown in Figure 10, and the data with the red mark are identified outliers.

In conclusion, the simulation results in Figure 6, Figure 8 and Figure 10 show that the proposed algorithm can effectively check the rationality of radar measurement data and identify outliers. After many simulation statistics, the recognition accuracy of outliers can reach more than 95%.

Conclusion

In this paper, we establishes a method to check and verify the rationality of pulse radar data based on single optical theodolite angle measurement data, which breaks through the limitations of traditional optical theodolites that require "two or more theodolites" when checking pulse radar. In other words, this method only requires one optical theodolite to calibrate or verify the tracking data quality of pulse radar. The simulation results show that when the radar ranging data is normal, the radar angle measurement data is normal, or the quality of the radar measurement data is unknown, the method can effectively identify the outlier in the measurement data sequence, with an accuracy rate of more than 95%, which has important engineering application value for the data quality assessment of the pulse radar in the process of performing measurement and control tasks.

Acknowledgement

This paper is financially supported by Guangdong Natural Science Foundation (2023A1515012341) and the Maoming Natural Science Foundation (2020S004).

References

1. Jianjuan X, et al. System error real-time estimation of radar network based on iterative generalized least squares. IEEE. 2022:6-10.

   [Crossref][Google scholar]

2. Liu L. External trajectory measurement data processing [M]. National Defense Industry Press. 2002:2.

   [Google scholar]

3. Guodong YU, et al. Global least squares algorithm for multi station rendezvous of optical theodolites [J]. J  App Opt. 2017.

   [Crossref][Google scholar]

4. Zhao LR, et al. The method on the measurement of the aircraft attitude by the spatial cosines relationship of the single station and planes to the intersection the multi-station of electro-optical theodolite [C]. IEEE. 2010:143-146.

   [Crossref][Google scholar][EBSCO]

5. Hu S, et al. Data processing technology of pulse radar tracking measurement. National Defense Industry Press. 2007.

   [Crossref][Google scholar]

6. Wu N. Joint positioning method of radar and theodolite. J Testi Tech. 2012;26:452-454.

   [Google scholar]

7. Cui S, et al. Data processing of optical tracking measurement. National Defense Industry Press. 2014:11.

   [Google scholar]

8. Liu X. Research on data processing method of spacecraft exterior trajectory measurement. Xi'an University of Technology. 2020.

   [Google scholar]

9. Liu S. Research on tracking algorithm of rocket flying orbit target. Xi'an University of Technology. 2020.

   [Google scholar]

10. Hu S, et al.  Comparative analysis and fault detection technology and its application in aerospace engineering. J Air Force Eng Uni. 2007;8:1-4.

    [Google scholar]

11. Liang J, et al. Fault tolerant minimum distance sum of squares positioning method for joint tracking of multiple optical theodolites. Optical and Precision Engineering. 2020.

    [Crossref][Google scholar]

12. Ling X, et al. Iterative parameter estimation for signal models based on measured data. Circuits, Systems, and Signal Processing. 2018;37:3046-3069.

    [Crossref][Google scholar][EBSCO]