Mining Big Sources using Efficient Data
Mining Algorithms

Shoban Babu Sriramoju

Mining Big Sources using Efficient Data Mining Algorithms

Shoban Babu Sriramoju
Associate Professor, Department of Computer Science and Engineering, Varadha Reddy Engineering College, Warangal, India ¹

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Data mining algorithms are widely used in the real world application in order to discover knowledge from large data sources. These algorithms work on historical data to analyze data in order to bring about trends or patterns. Association rule mining or frequent item set mining is very useful in applications like inductive databases, query expansion and others. A frequent itemset is the itemset when a set of records are repeated for specified number of times in a given dataset. When such frequent itemset is no present in other frequent itemset, it is named as maximal itemset. When it is not as part of other itemset, them it is called closed itemset. These itemsets are used to extract patterns or trends in the real world applications that support in decision making. Recently Uno et al. proposed data mining algorithms to discover maximal itemsets, closed itemsets and frequent itemsets. In this paper we practically explore those algorithms. We implement them in a prototype application and the empirical results reveal that they are very useful for many data mining solutions.

Keywords

Data mining, big databases, association rule mining, frequent itemsets

INTRODUCTION

For many years data mining is the domain which provided techniques or algorithms for processing huge amount of data in order to obtain meaningful information that helped in making well informed decisions. With these techniques expert systems have been built that are used to make high quality decisions. The data mining techniques that have been used in the real world include K-means, C4.5, Apriori, Expectation Maximization, Page Rank, kNN, AdaBoost, Support Vector Machine (SVM), CART (Classification and Regression Trees) and Naïve Bayes algorithm. These are in the top 10 algorithm that exists in the world for knowledge discovery. Apriori, for instance, is used to obtain frequent patterns that can be used in decision making. C4.5 is used for making clusters of given objects while K-means is also used for doing the same and it is one of the famous clustering algorithms.

Association rule mining and frequent itemset mining is very useful technique in data mining domain. It discovers the frequently repeated itemsets in the given data source as per the given support and confidence. Generally domain experts provide the required support and confidence. The applications of such technique include query expansion, association rule mining and inductive databases. Implementations of frequent itemsets [1], [2] can be used to mine huge amount of business data in order to make policies that can help companies in the long run. The business intelligence thus obtained can help making profits so as to excel in business. Therefore mining actionable knowledge has very important utility in the real world.

Recently Uno et al. [3] proposed algorithms for discovering itemsets. These algorithms can obtain closed itemsets, frequent itemsets and closed itemsets [4], [5] and [6]. These algorithms are very useful as they are efficient in obtaining essential knowledge. In this paper these algorithms are practically implemented using Java as development platform. The prototype application we built to demonstrate the efficiency of algorithms [7] is user friendly. The experimental results revealed that the application is very useful in the real world for efficient decision making. The remainder of this paper is structured as follows. Section II provides preliminaries pertaining to itemset mining. Section III provides details of proposed algorithms. Section IV presents prototype information. Section V presents experimental results while section VI concludes the paper.

LITERATURE SURVEY

Itemset is nothing but a set of items that can be denoted as I = {1, 2,3, …, n}. Consider T represents a transaction datasets which has many records that are denoted as T= {t1, t2, t3, …, tn). Consider an itemset P for illustration of an example. When any transaction contains P which is known as the occurrence of P which is denoted as T(P) which represents all transactions in the given dataset. The frequency of P can be denoted as |T(P)| which can also be represented as frq(P). The frequency is considered when the given confidence and support are satisfied [8]. When frequent itemset is not as part of any other frequent itemset, such one is known as maximal itemset [9]. When any itemset is not a part of any other itemset, it is known as closed itemset.

ALGORITHMS

The data mining algorithms presented recently by Uno et al. [10] are explored here. These algorithms are used to obtain maximal itemsets, closed itemsets and frequent itemsets. Figure 1 shows an algorithm that is used to mine the frequent itemsets.

As shown in Fig. 1, it is evident that the algorithm executes in recursive fashion. It is a recursive mechanism as it invokes itself every time. It takes dataset as input and generated frequent itemsets that are represented by P. Figure 2 presents an algorithm that is used to extract closed itemsets.

As shown in figure 2, closed itemsets are extracted by this algorithm. The algorithms work on given dataset in order to generate closed itemsets as output that satisfies given support and confidence. Figure 3 presents an algorithm that can generate maximal itemsets

As shown in figure 3, the algorithm takes dataset as input and works on it for computing maximal datasets. The results generated by the algorithm are as per the given support and confidence given by the domain expert.

BUILDING PROTOTYPE

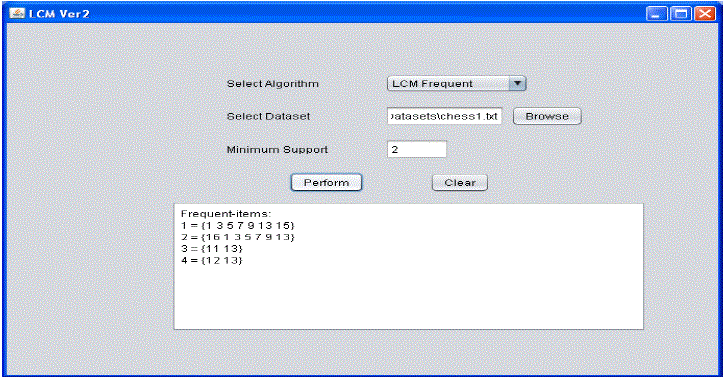
We built a prototype application that is used to test the efficiency of the implemented algorithms. The application has been built in Java platform which provides user-friendly interface. The environment used to build the application includes a PC with 4GB RAM, Core 2 dual processor running Windows 7 operating system. The prototype is meant for performing various mining operations such as mining closed itemsets, frequent itemsets, and maximal itemsets. The results of algorithm can be viewed in figure 4.

As seen in figure 4, user is given interface for choosing any algorithm and dataset. When user selects dataset and chooses frequent itemsets as algorithm, the extracted itemset is presented in text area provided. Minimum support is the basis for extracting the result. Figure 5 presents the results of another algorithm that returns closed itemsets.

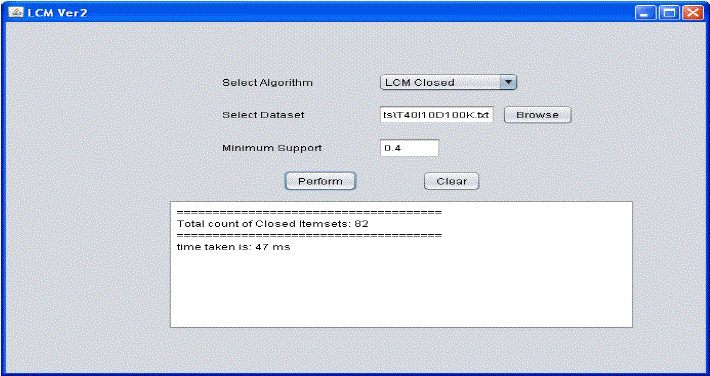
As seen in figure 5, data set and algorithm are selected by user. Closed itemsets is the result of the algorithm. Figure 6 presents the result of algorithm that produces maximal itemsets. The results also reveal the time taken to discover maximal itemsets.

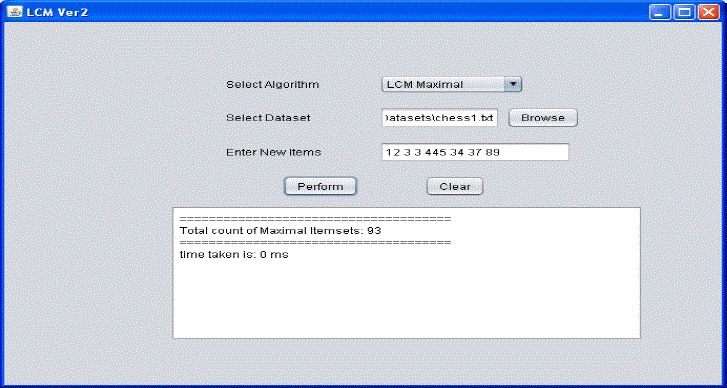
As shown in figure 6, user is given provision to choose algorithm and dataset. The data mining algorithm for extracting maximal itemsets works on the given data and produces results in text area. The algorithm also takes some additional data items as input from end user. The closed itemsets are presented.

EXPERIMENTAL RESULT

Various datasets are used with our prototype application in order to make certain experiments. The results thus obtained are also compared with other algorithms of this paper and the ones came prior to this paper. In all experiments the application captures minimum support from a domain expert. The results are presented as follows.

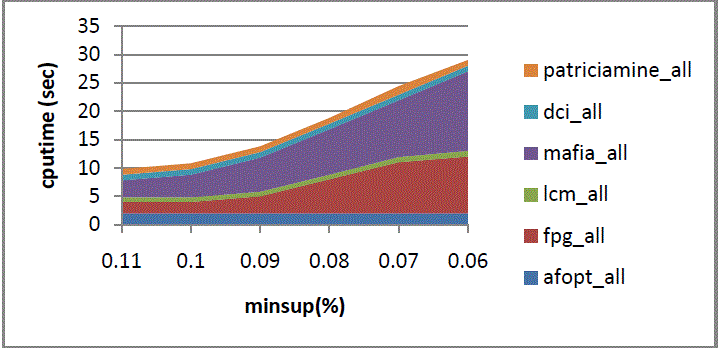
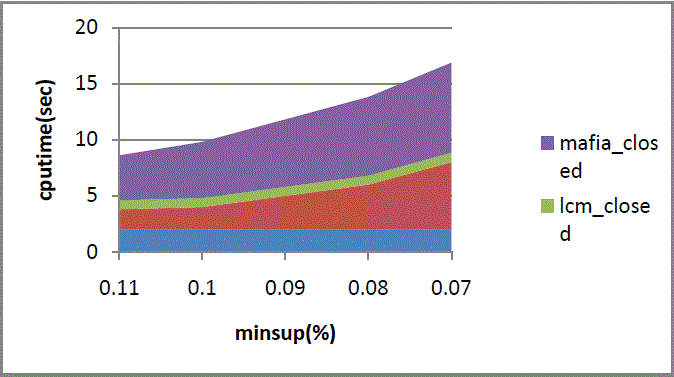
As shown in fig 7. Represents the horizontal axis represents minsup while vertical axis represents cpu time.

As shown in fig. 8. Represents the horizontal axis represents minsup while vertical axis represents cpu time.

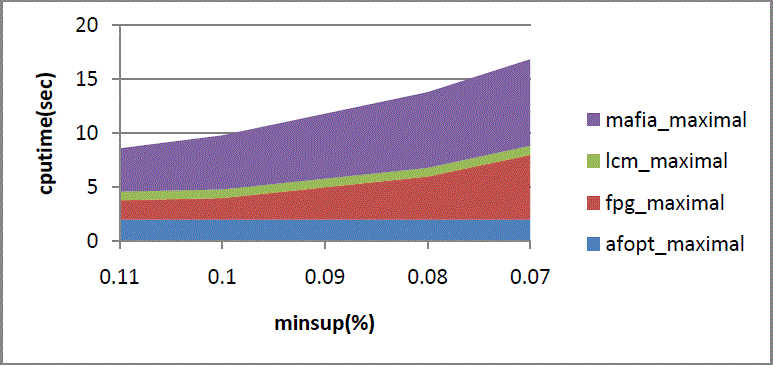
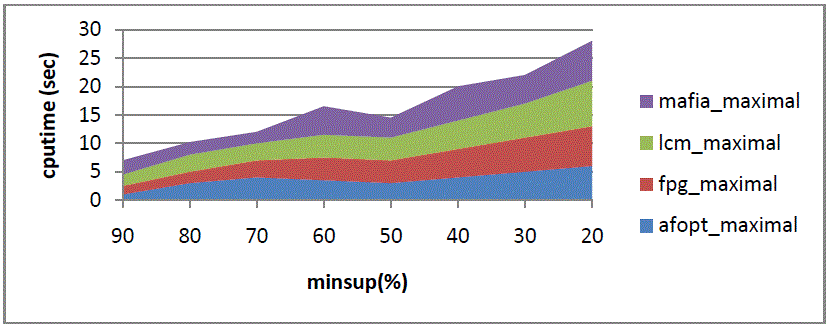
As shown in fig. 9. Represents the horizontal axis represents minsup while vertical axis represents cpu time.

As shown in fig. 10. Represents the horizontal axis represents minsup while vertical axis represents cpu time.

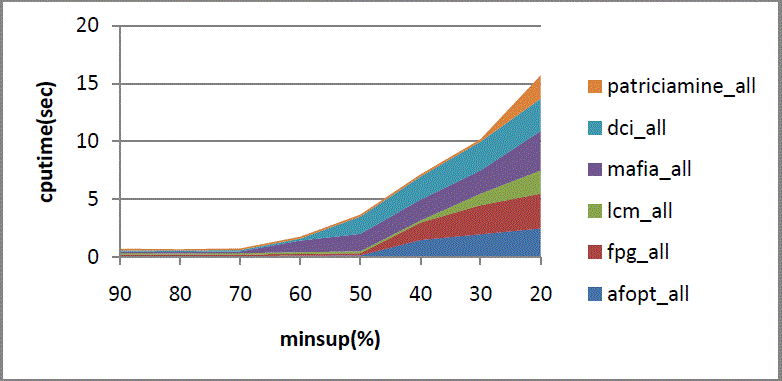
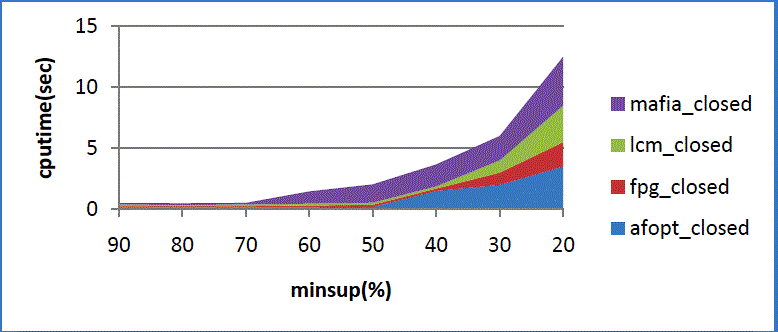
As shown in fig.11. Represents the horizontal axis represents minsup while vertical axis represents cpu time.

As shown in fig. 12. Represents the horizontal axis represents minsup while vertical axis represents cpu time.

CONCLUSION

In this paper we studied many data mining algorithms for extracting business intelligence. We implemented algorithms that are recently proposed by Uno et al. [3] for extracting frequent itemsets, maximal itemsets and closed itemsets. These itemsets are used to make expert decisions in real time applications. The algorithms produce actionable knowledge that can be used to make effective decisions. We built a prototype application that demonstrates the effectiveness of the algorithms. The empirical results are encouraging.

Figures at a glance


Figure 1	Figure 2	Figure 3	Figure 4


Figure 5	Figure 6	Figure 7	Figure 8


Figure 9	Figure 10	Figure 11	Figure 12

References

R. Agrawal and R. Srikant, “Fast Algorithms for Mining Association Rules in Large Databases," In Proceedings of VLDB '94, pp. 487{499, 1994.

R. Agrawal, H. Mannila, R. Srikant, H. Toivonenvand A. I. Verkamo, “Fast Discovery of Association Rules," In Advances in Knowledge Discovery and Data Mining, MIT Press, pp. 307{328,1996.

Takeaki Uno, Masashi Kiyomi and Hiroki Arimura, “LCM ver. 2: E_cient Mining Algorithms for Frequent/Closed/Maximal Itemsets”.

E. Boros, V. Gurvich, L. Khachiyan, and K. Makino, “On the Complexity of Generating Maximal Frequent and Minimal Infrequent Sets," STACS 2002, pp. 133-141, 2002.

D. Burdick, M. Calimlim, J. Gehrke, “MAFIA: A Maximal Frequent Itemset Algorithm for Transactional Databases," In Proc. ICDE 2001, pp. 443-452, 2001.

D. Burdick, M. Calimlim, J. Flannick, J. Gehrke, and T. Yiu, “MAFIA: A Performance Study of Mining Maximal Frequent Itemsets," In Proc. IEEE ICDM'03 Workshop FIMI'03, 2003. (Available as CEUR Workshop Proc. series, Vol. 90, http://ceur-ws.org/vol-90)

G. Grahne and J. Zhu, “Effciently Using Pre_x-trees in Mining Frequent Itemsets," In Proc. IEEE ICDM'03 Workshop FIMI'03, 2003. (Available as CEUR Workshop Proc. series, Vol. 90, http://ceur-ws.org/vol-90)

J. Han, J. Pei, Y. Yin, “Mining Frequent Patterns without Candidate Generation," SIGMOD Conference 2000, pp. 1-12, 2000

R. Kohavi, C. E. Brodley, B. Frasca, L. Mason and Z. Zheng, “KDD-Cup 2000 Organizers' Report: Peeling the Onion," SIGKDD Explorations, 2(2), pp. 86-98, 2000.

R. J. Bayardo Jr., “Efficiently Mining Long Patterns from Databases", In Proc. SIGMOD'98, pp. 85{93, 1998.

Takeaki Uno, Tatsuya Asai, Yuzo Uchida and Hiroki Arimura, “LCM: An Efficient Algorithm for Enumerating Frequent Closed Item Sets”.