International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Modeling and Control of Chemical Reactor Using Model Reference Adaptive Control

Padmayoga.R1, Shanthi.M2, Yuvapriya.T3
  1. PG student, Dept. of Electronics and Instrumentation, Valliammai Engineering College, Chennai, India
  2. Assistant Professor, Dept. of Electronics and Instrumentation, Valliammai Engineering College, Chennai, India
  3. Assistant Professor, Dept. of Electronics and Instrumentation, Valliammai Engineering College, Chennai, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Chemical processes are highly nonlinear in nature. The major drawback of non-adaptive control systems is that these control systems cannot cope with the fluctuations in the parameters of the process. The solution for such problem can be addressed by the use of high feedback gain in certain levels to decrease the sensitivity of the control system. Generally, high gain controllers come across two problems that are cited to be major. They are: large signal magnitude and closed loop instability. To overcome this issue, a control system has to be developed which adapts to the changes in a process. In this paper, the adaptive controller is modeled for a chemical reactor. The adaptive controller is modeled using MATLAB/ SMULINK and its performance is compared with other controller performances

Keywords
Process control-Chemical reactor, modelling, PID controller, adaptive controller.

INTRODUCTION
In common sense, ‘to adapt’ denotes the change in behaviour to confirm new circumstances. An adaptive controller is a controller that can modify its behaviour in response to the changing dynamics of the process and the character of the disturbances. The core element of all the approaches is that they have the ability to adapt the controller to accommodate changes in the process. This permits the controller to maintain a required level of performance in spite of any noise or fluctuation in the process. An adaptive system has maximum application when the plant undergoes transitions or exhibits non-linear behaviour and when the structure of the plant is not known. Gain scheduling is one form of adaptive control but it requires knowledge about all the process to be effective. Another alternative is to adapt the controller’s Parameters or when a model is available to use the model identification error to tune the controller’s parameters. The purpose of this paper is to design and simulate a Model Reference Adaptive control (MRAC) for a single inputs single outputs chemical reactor.

TYPES OF ADAPTIVE CONTROL
Generally there are two different mechanisms for the adaptation of the controller parameters. Programmed or scheduled adaptive control and self –adaptive control. Adaptive control systems have been applied in chemical process. There are two main reasons for adaptive controller. First, most chemical processes are non-linear. Second, most of the chemical processes are non-stationary (i.e. their characteristics changes with time).

A) Programmed or scheduled adaptive control
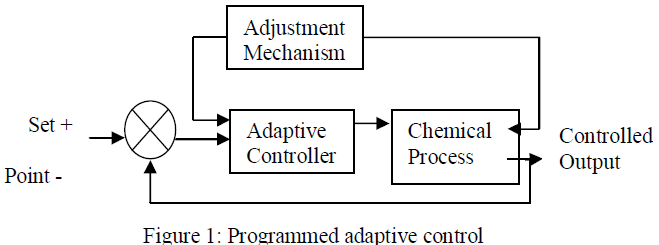
Figure 1 shows the block diagram of a programmed adaptive control system. It is composed of two loops. The inner loop is an ordinary feedback control loop. The outer loop includes the parameters adjustment (adaptation) mechanism and it is comparable to feed forward compensation.
image

MODEL REFERENCE ADAPTIVE CONTROL
Model reference adaptive controller (MRAC) is a controller used to force the actual process to behave like idealized model process. MRAC systems adapt the parameters of a normal control system to achieve this match between model and process.

A. Core elements of model reference adaptive control
The basic structure of MRAC system is shown in figure 2.
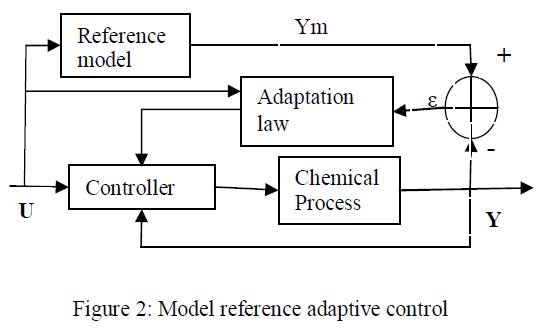image
The standard implementation of MRAC based systems contains the four key blocks shown above. The reference model defines the desired performance characteristics of the process being controlled. The adaptation law uses the error between the process and the model output, the process output and input signal to vary the parameters of the control system. These parameters are varied so as to minimize the error between the process and the reference model. The control system can be anything from a simple gain based controller to a more complicated parameter based transfer function or plant matrix. The final element of the MRAC system is the process that is being controlled.

B. Adaptation law
The adaptation law uses the input signal, the output of the plant and the error between the plant and reference model outputs. These three signals are used to adapt the parameters of the selected controller. The adaptation law attempts to find a set of parameters that minimize the error between the plant and the model outputs. To do this, the parameters of the controller are incrementally adjusted until the error has reduced to zero. A number of adaptation laws have been developed to date. The two main types are the gradient and the Lyapunov approach.
i. GRADIENT METHOD
ii. Lyapunov method
An alternative approach to the MIT rule is to use a Lyapunov based method, which avoids the stability problems present in the gradient approaches. A typical adaptation law for a Lyapunov based adaptive controller is shown in equation 3.1 below,
image
The major difference between the MIT rule and the Lyapunov method is that the sensitivity of the error to a specified parameter de/dt has been replaced by the actual value of the parameter,θ.

MATHEMATICAL MODELING
A perfectly mixed continuously stirred tank reactor (CSTR) as shown in figure 3 with first order exothermic irreversible reaction A B is considered. In this a fluid stream is continuously fed to the reactor and other fluid stream is continuously removed from the reactor. A jacket surrounding the reactor has in feed and exit streams. The jacket is assumed to be perfectly mixture and at lower temperature then reactor temperature. Energy passes through the reactor walls into jacket removing the heat generated reaction.
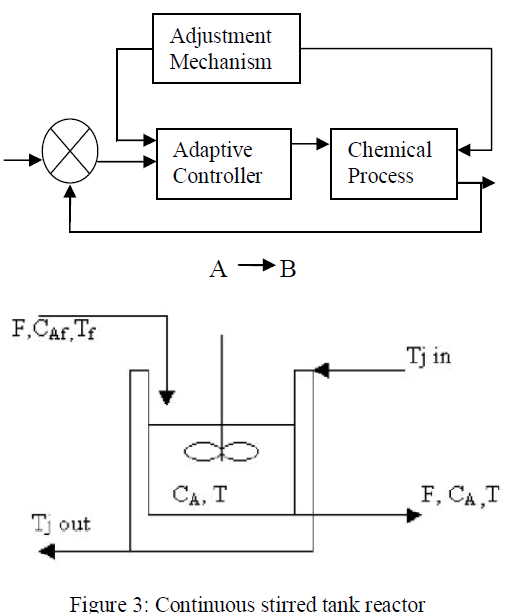image
Put together, the CSTR has three input signals:
CAf = Concentration of feed stream.
Tf = Inlet feed stream temperature.
Tj = Jacket coolant temperature.
And two output signals:
CA= Concentration of A in reactor tank.
T = Reactor temperature.

A) Over all material balance
The CSTR system is modelled using basic accounting and energy conservation principles.
Rate of material accumulation = rate of material in – rate of material out.
image
Assuming a constant amount of material in the reactor,
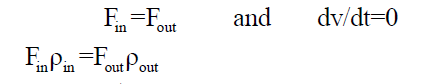image
3.1) Balance on component A
The balance on component A is,
image
Where r is the rate of reaction per unit volume.
3.2) Energy balance
The energy balance equation is,
image
Where T represents an arbitrary reference temperature for Enthalpy.

B) Steady state solution
To solve these two equations, all parameters and variables except for two (CA and T) must be specified. Given numerical values for all of the parameters and variables, we can use Newton’s method to solve for the steady state values of CA and T.
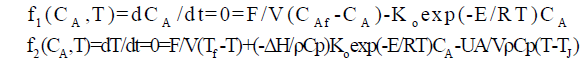image

C) Guess1
High concentration (low conversion), Low temperature. Here we consider an initial guess of CA =8 and T = 300
K.The steady state solution for guess is that is, high concentration (lowconversion) and low temperature. The parameter values are as shown in table 1.
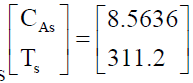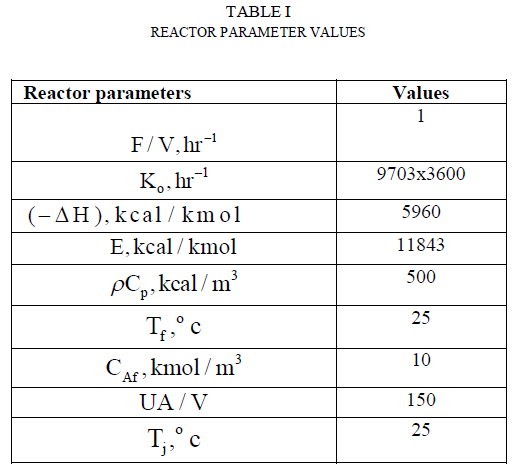image
image
Let the state, and input variables be defined in deviation variable form,
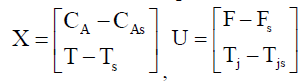image

NON ADAPTIVE CONTROL ANALYSIS
The PID controller algorithm involves three separate constant parameters and is accordingly sometimes called three term control: the proportional P depends on the present error; the integral I depends on the accumulation of past errors; the derivative D depends on the prediction of future errors based on current rate of change. The simplified transfer function model is,
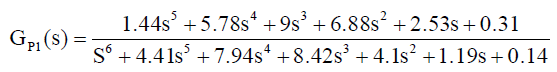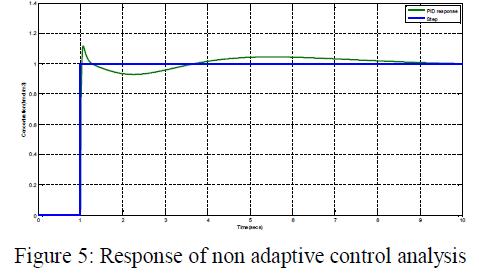
image
The response of non adaptive control is shown in figure 5,
image

INTERNAL MODEL CONTROL
The internal model control (IMC) philosophy relies on the internal model principle which states that control can be achieved only if the control system encapsulates, either to be implicitly or explicitly, some representation of the process to be controlled. In particular if the control scheme has been developed based on the exact model of the process, then the perfect control is theoretically possible. The process model is explicitly used in the control system design procedure. This IMC controller having λ is the tuning parameter.
Gc(s) =GP(s)-1
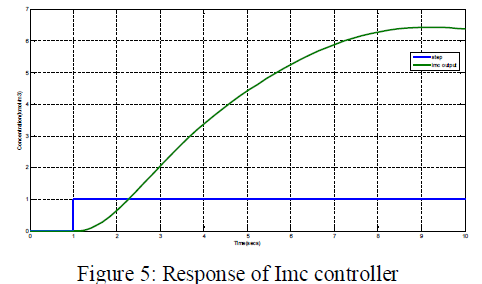
And if Gp=Gp (the model is an exact representation of the process).Then it is clear that the output will always be equal to the set point. Notice that this ideal control performance is achieved without feedback (as encapsulated in the process model) being controlled, we can achieve perfect control. It also tells us that feedback control is necessary only when knowledge about the process is inaccurate or incomplete. The response of IMC controller as shown figure 5,
image

ADAPTIVE CONTROL DESIGN AND SIMULATION
This section provide three sets: the first covers the design of model reference adaptive control and its implementation in simulink. The second and the third compare the performance of an adaptive control to a conventional controller without noise and with noise respectively. This section provide three sets: the first covers the design of model reference adaptive control and its implementation in simulink. The second and the third compare the performance of an adaptive control to a conventional controller without noise and with noise respectively.
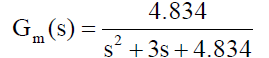image

A) Comparison without noise
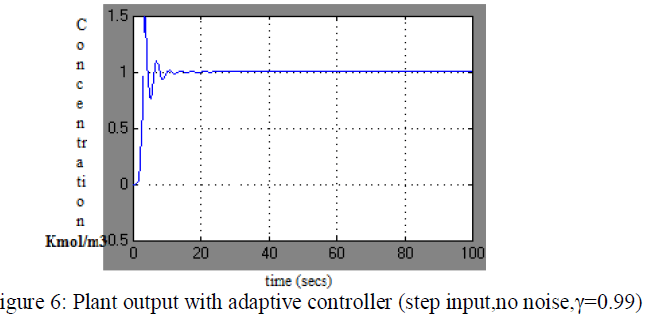
The first task we perform to compare the standard controller with adaptive controller for step input and no noise. The response is shown in fig 6,
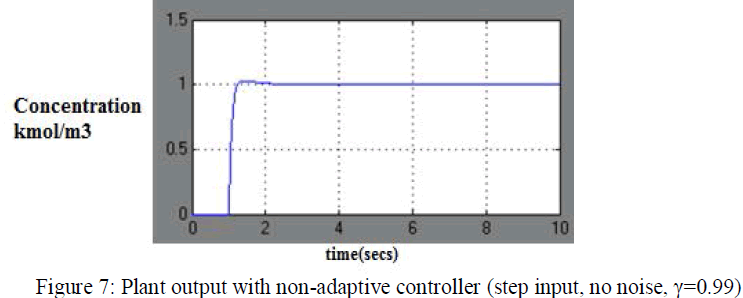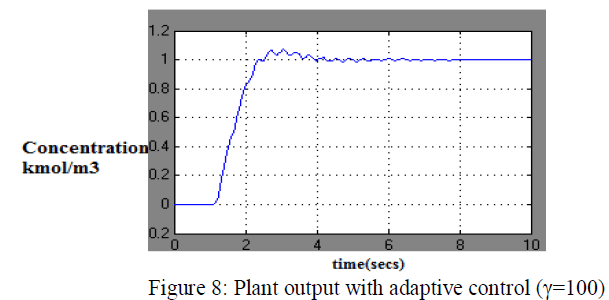
image
image
In these graphs one major disadvantage of adaptive control is immediately apparent. The adaptive controller takes 20 secs to match the output of reference model and the non adaptive controller matched with in 2 secs. The overshoot of adaptive controller is excessive (5%) and for non adaptive controller is below 3%.To overcome this problem is to increase the adaptation gain (γ).For example, increasing adaptation gain responses as shown in figure 8 and 9.
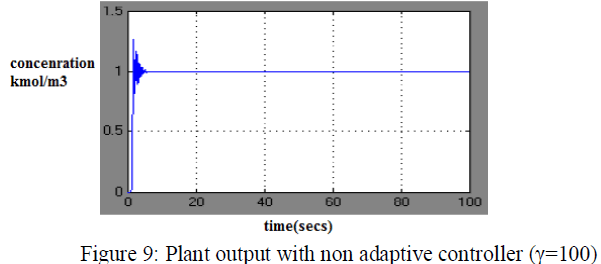image
image
This has improved the overshoot to below 10% and the settling time is less than 10 seconds. Further increase the adaptation gain does not result in an improvement of the system.
B) Comparison with noise
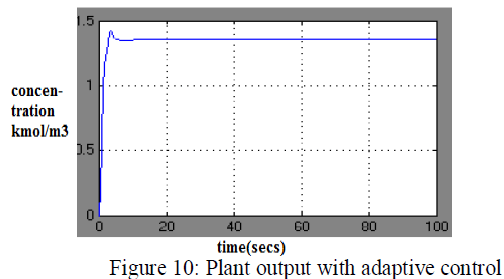
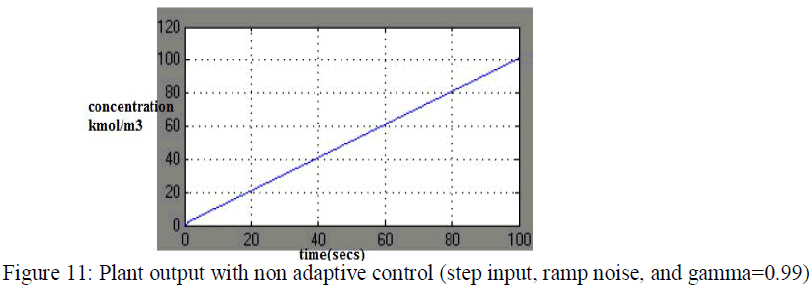
The next task to compare the performance of two controllers in the presence of ramp noise as shown in fig 10 and 11,
image
image

CONCLUSION
The non adaptive model can provide speed whenever its parameters are close to those of the process. The non adaptive controller may not provide a satisfactory closed loop control. So we go for next controller which is IMC controller. The internal model control (IMC) philosophy relies on the internal model principle which states that control can be achieved only if the control system encapsulates, either to be implicitly or explicitly, some representation of the process to be controlled. It is difficult to implement for higher order system and it does not gives the accurate response. For this reason we preferred adaptive controller. The adaptive controller exhibits superior performance in the presence of noise and convergence time is typically large and there is a large overshoot. These two problems are due to the adaptive controller failing to adapt fast enough to force the plant to match the model. Increasing the adaptation rate improves the performance of the adaptive controller at cost of increased oscillation.

References
  1. Rahul Upadhyay and Rajesh Singla,"Application of adaptive control in a process control",2nd international conference on education technology and computer(ICETE),20 10.(IEEE).
  2. R.Aruna and M.Senthil kumar,”Adaptive control for interactive thermal process”proceedings of TCTECT,2011 (IEEE).
  3. S.Jegan,K.Prabhu,"Temperature control of CSTR process using adaptive control", International Conference on Computing and Control Engineering(TCCCE),2012.
  4. B.Wayne Bequette, process dynamic modeling, analysis and simulation; Precentice Hall: NJ, 1998.
  5. George stephanopolus, chemical process control; prentice Hall of India private limited, NewDelhi, 2002.
  6. KJ. °Astrom and B. Witten mark, Adaptive control, Addison Wesley,1995.
  7. William L.Luyben; process modeling, simulation and control for chemical Engineer; MCGraw-Hill, Inc., 1990.
  8. Dwayne Tyner; Masoud Soroush; adaptive temperature control of multi product jacketed reactor.Ind.Eng.Chem.Res.1999, 38,4337-4344.
  9. Garcia,C.E. and Morari.M., “Internal Model Control - UnifyingReview and Some New Results”, Industrial Engineering Chemical Process Design and Development, vol. 21,1982.
  10. Narendra kumar and Neha kanduja,”Mathematical modellind and simulation for CSTR usin MIT rule”.IEEE trans. 978-1-4673-0934- 9/12/$3l.00 ©2012 IEEE.