Keywords
|
| PI tuning, IMC (Internal Model Control), GA (Genetic Algorithms), MATLAB Simulink |
INTRODUCTION
|
| In any of the process control and automation industries, controller designing and the automatic control is the most important part. The aim of this paper presents the analysis of temperature process control and robust controller. Control or maintaining the temperature at a desired state is an important and common task in all process industries. Traditional controllers are easy to understand and implement. PID controllers are applicable to many control problems, but they can perform poorly in some control applications. It suffers deficiencies in the face of plant non-linearities and uncertainty presents in the plant. This conventional techniques were unable to give satisfactory results for the process output. Model based control and an internal model based PID controller is developed to control the temperature of the process [1] [2]. IMC is a practical control design strategy that is employed in many advanced control system design packages. The proposed method incorporates this method in IMC and implementing the IMC within a conventional PID controller framework [1]. Among the other tuning methods, IMC PID controllers tuning methods has gained widespread acceptance in the process industries because of its easy in design and simple in understand, robustness and fast in real time applications. |
| In past few decades, intelligent techniques have been used to meet the system demands. An intelligent agent is a system that perceives its environment and takes actions which maximizes its chances of success. Neural network and fuzzy logic mimic the functioning of the human intelligence process [6]. However their real time implementation is quite difficult [7]. On the other hand optimization algorithms have also received increasing attention by the research community as well as the industry [8]. The advantage of optimization algorithms over neural controllers is that they can be incorporated in PID tuning with ease and simplicity. Control design is called “optimal control” when a predefined criterion is optimized [11].Optimality is just with respect to the criterion at hand and the real performance depends on the suitability of the chosen criterion [8]. |
| In section 2, we have discussed in detail about the development of the mathematical model for the temperature process control. The controllers tuning results of conventional techniques are discussed in section 3. Section 4 and 5 deals with the explanation of the optimization techniques Genetic Algorithm and its implementation. The controllers comparative studies and results are given in Section 6. The conclusions arrived, based on the results is given in Section 7. |
TEMPERATURE PROCESS
|
| The temperature controllers are able to control the temperature of any plant. Here the process is a liquid tank with a heater and with two temperature sensors. The temperature sensor used in this process is type RTD, Pt 100. The liquid inside the process tank is controlled by the controller. A temperature control system continuously monitor the inlet temperature and the outlet temperature of the liquid tank [3]. Typically it contains a controller unit, temperature input unit and control output unit. The Analog-to-digital (ADC) unit together with temperature sensor forms the temperature input unit and the solid state relay driver forms the control output unit. |
| The temperature process model on which the simulator is based on the first order model, based on the energy balance equation under the assumption of homogenous conditions of the liquid in the process tank. The process model taken in this paper contains a time delay. Which represents the delay exists between an excitation of the heating element and the response in the temperature sensor [3]. In addition the simulator contains a first order transfer function representing a time constant in the heating element. The FOPDT model of the temperature process is given by: |
 |
| Temperatures often have to be set on large machines or process or systems. The setting should not change the process parameters when faults occur [3]. Such tasks are undertaken by a closed-loop controllers. The controlled variable is first measured and an electrical signal is created to allow an independent closed-loop controller to control the process variable. The measured value in the controller must then be compared with the desired value of the process or the desired-value curve. The result of this comparison determines any action that needs to be taken for the process. Finally a suitable location must be found in the system where the controlled variable can be influenced by the controller. In the temperature closed-loop control system the task is to keep the outlet temperature at the desired value or to follow the desired-value curve. |
| Mathematical Modelling |
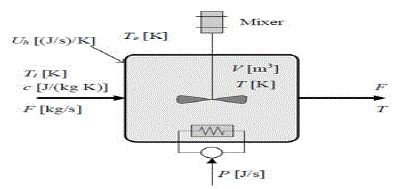
| The development of a process model is an important part in all modeling systems. It is an vital role that a framework be used the development of a process model which is adequate and accurate for the purpose. Construction of a process or system model with its physical parameters is called as a modeling. Precise temperature control is a challenge faced by all process industries. A practical temperature process system is a highly non-linear and sluggish in nature and the process modeling becomes complex for larger systems. Figure 2 shows a liquid tank with heater coil, continuous liquid flow and heat transfer to the environment through the tank walls. The liquid delivers power through a heater coil. P is a power from the heater. T is a temperature in the process tank. Tin is the temperature in the inlet flow. Tout is the temperature outlet. W is a mass flow. C is a specific heat capacity. ρ is a density and U is a total heat transfer coefficient. |
| From this inputs and outputs parameters relations, and with some assumptions, such as the inflow and the outflow of the tank are equals, and there is no storage of thermal energy in the heater coil. This means that all of the supplied power to the heating element is supplied to the liquid tank. The process model for the temperature process is based on the energy balance equation which is given by: |
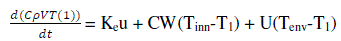 (1) (1) |
| In practice there is a time delay between an excitation in the heater and the response in the temperature sensor. By taking the Laplace transform of the process model above we can get the following transfer function from the control signal to the “Temperature (T)” is: |
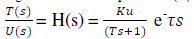 |
| We assume that this time delay is inversely proportional to the mass flow rate W. This is a process as first order model with time delay. Thus for the temperature process, the model has Gain, Time Constant and Time Delay. It is given by the following equation as: |
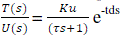 |
| For fixed input heater supply the temperature is allowed to increase to the desired level from 0°C. At each sample time the data from the thermocouple between 4-20 mA is collected. The RS-232 serial port the data are collected and fed to the process. The obtained response from the constant input heater supply is called Process Reaction Curve (PRC). From the PRC curve the process is modeled and approximated as First Order plus Delay Time (FOPDT) process which includes “Gain K”, “Time constant τ” and “Dead time td”. Then this experimental data are approximated to be a FOPDT model and the identified model of the temperature process is as follows: |
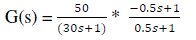 |
CONVENTIONAL DESIGN TECHNIQUES
|
| The basic PI controller parameters are given as, proportional gain, Kp and integral gain Ki. Over the last fifty years, numerous methods have been developed for setting the parameters of a PID controller. In this paper it is considered to proceed with IMC tuning technique proposed by Skogestad for PI tuning. IMC involves a different structure and controller, a single “IMC” can be used for multivariable systems and it has zero steady-state offset for “step-like” inputs. |
| Internal Model Control Tuning Technique The Internal Model Principle |
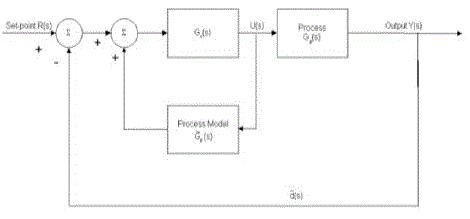
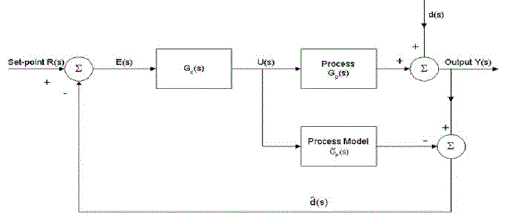
| The Internal Model Control (IMC) philosophy relies on the Internal Model Principle, which states that control can be achieved only if the control system encapsulates, either implicitly or explicitly, of the process to be controlled [1] [7]. Here the control scheme has been developed based on the exact model of the process system, and then the perfect control is theoretically possible in this advanced method. The controller has been developed based on the model, so it is named as the Internal Model Control. |
| A controller Gc(s) is used to control the process Gp(s). Suppose ÃÅÃÆp(s) is a model of Gp(s). By setting Gc(s) to be inverse of the model of the process, Gc (s) = ÃÅÃÆ (s) – 1 and if Gp (s ) = ÃÅÃÆ (s), (the model is an exact representation of the process) The process output is exactly equal to the set point. The ideal performance of the controller is achieved without any feedback requires. |
| The IMC Strategy |
| In practice, however, the process and the model mismatch is common in all real time implementation; the process model may not be invertible and the system is often affected by unknown disturbances. The open loop control arrangement will not be able to maintain output at a set point [1]. Nevertheless, it forms the basis for the development of a control strategy that has the potential to achieve perfect control for the system. This strategy is known as a IMC (Internal Model Control). |
| From this closed loop expression, Gc (s) = ÃÅÃÆ (s) – 1, and if Gp (s ) = ÃÅÃÆ (s), then perfect set point tracking and disturbance rejection is achieved. If Gp (s) ÃÅÃÆ (s), perfect disturbance rejection can still be realized provided Gc (s) = ÃÅÃÆ (s) – 1. |
| To improve robustness of the controller, the effects of process model mismatch should be minimized. This mismatch usually occur at the high frequency range and at the end of the system frequency response, Gf(s) a low-pass filter is usually added to attenuates the effects of process model mismatch. Thus the IMC is usually designed as the inverse of the process model in series with a low-pass filter, that is GIMC (s) = Gc (s) Gf (s). |
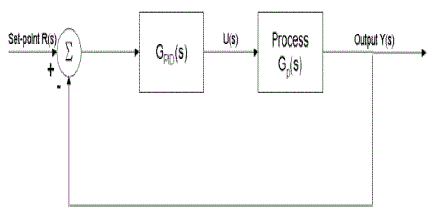
| The IMC PID Controller |
| The most common used industrial controller is still the Proportional Integral and Derivative controller. It gives a transparent framework for a control system designs and tuning [2]. Here IMC PID is implemented in this paper. It is an advanced control concept. By using this controller concept it will gives the perfect control and stable results. It is a two degree controller. Which gives both the set point tracking and disturbance rejection [2]. The purpose of the IMC PID controller is achieved by the IMC block diagram rearrangement to the form of a standard feedback closed loop control. In IMC law, for a number of common process transfer functions, it is equivalent to PID-Type feedback controllers [7]. This use an approximation for time delays in order to find a PID-Type control law. |
 |
| And then to |
 |
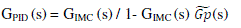 |
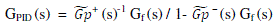 |
| For the first-order plus time-delay process it is given by |
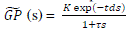 |
| This is the temperature process model with first-order plus time-delay |
| IMC- PID Control for Temperature Process Control |
The IMC PID design for the Temperature FOPDT process is:  |
 |
GA BASED PI CONTROLLER
|
GENETIC ALGORITHM
|
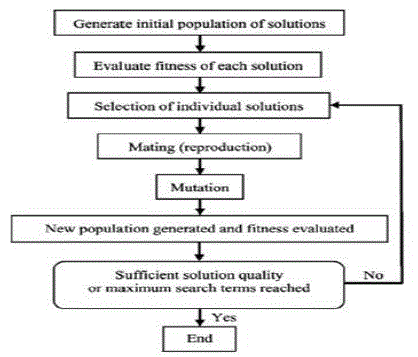
| `In Genetic algorithm is a powerful search algorithm that performs an exploration of the search space that evolves in analogy to the evolution in nature. They use probabilistic transition rules instead of deterministic rules, and handle a population of potential solutions known as individuals or chromosomes that evolves iteratively. Iteration of the algorithm is termed as generation. The evolution of solutions is simulated through a fitness function and genetic operators such as reproduction, crossover and mutation. The fittest individual will survive generation after generation, while also reproducing and generating offspring’s that might be stronger. At the same time, the weakest individuals disappear from each generation. |
| A genetic algorithm is typically initialized with a random population consisting of between 20 100 individuals. This population (mating pool) is usually represented by a real-valued number or a binary string called a chromosome. How well an individual performs a task is measured and assessed by the objective function. The objective function assigns each individual a corresponding number called its fitness. The fitness of each chromosome is assessed and a survival of the fittest strategy is applied. In this project, the magnitude of the error will be used to assess the fitness of each chromosome. There are three main operators for a genetic algorithm; these are known as reproduction, crossover and mutation. The flow chart for GA is given in Figure.5. |
IMPLEMENTATION OF GA
|
| The optimal values of the conventional PI controller parameters Kp and Ki, is found using GA. All possible sets of controller parameter values are chromosomes whose values are adjusted so as to minimize the objective function, which in this case is the error criterion, which is discussed in detail. For the PI controller design, it is ensured the controller settings estimated results in a stable closed loop system. |
| Initialization of Parameters |
| To start up with GA, certain parameters need to be defined. It includes the population size, bit length of chromosome, number of iterations, selection, crossover and mutation types etc. Selection of these parameters decides to a great extent the ability of designed controller [13-14]. The range of the tuning parameters is considered in the range of 0-10. Initializing the values of the parameters for this paper is as follows: |
| Population size – 100 |
| Bit length of the considered chromosome – 6 |
| Number of Generations – 100 |
| Selection method – ‘Maximum Geometric selection’ |
| Crossover type – ‘Single point crossover’ |
| Crossover probability – 0.8 |
| Mutation type –‘Uniform mutation’ |
| Mutation probability – 0.05 |
| Objective Function for the Genetic Algorithm |
| The objective functions considered are based on the error criterion. A number of such criteria are available and in this paper controller’s performance is evaluated in terms of Integral absolute error(IAE), Integral square error(ISE), Mean square error(MSE), Integral time absolute error (ITAE) error criteria. In this paper we consider the limits for the equation from time, t=0 to t=Ts, where Ts is the settling of the system to reach steady state condition for a unit step input. |
| In the fig 1, it shows the graph of time Vs throughput of receiving packet. Throughput is the average rate of successful message delivery over a communication channel. |
| Termination Criteria |
| Termination of optimization algorithm can take place either when the maximum number of iterations gets over or with the attainment of satisfactory fitness value. Fitness value, in this case is nothing but reciprocal of the magnitude of the objective function, since we consider for a minimization of objective function. In this paper the termination criteria is considered to be the attainment of satisfactory fitness value which occurs with the maximum number of iterations as 100.c |
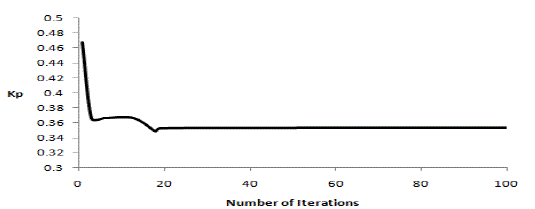
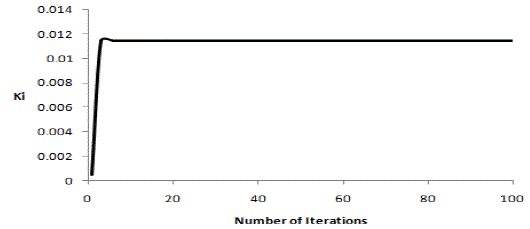
| For each iteration the best among the 100 particles considered as potential solution are chosen. Therefore the best values for 100 iterations is sketched with respect to iterations, and are as shown in Figs. 6 and 7. |
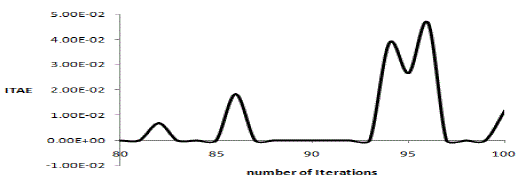
| The PI controller was formed based upon the respective parameters for 100 iterations, and the global best solution was selected for the set of parameters, which had the minimum error. A sketch of the error based on ITAE criterion for 100 iterations is as given in Fig.8. |
| It was seen that the error value tends to decrease for a larger number of iterations. As such the algorithm was restricted to 100 iterations for beyond which there was only a negligible improvement. Based on GA for the application of the PI tuning we get the PI tuning parameters for the model as Kp=0.02975, Ki = 0.000975. |
RESULTS AND COMPARISON
|
| In this section the tuned values through the traditional as well as the proposed techniques are analyzed for their responses point of 15 cm. A tabulation of the time domain specifications comparison and the performance index comparison for the obtained models with the designed controllers is presented. |
| Simulated Response of the Temperature Process |
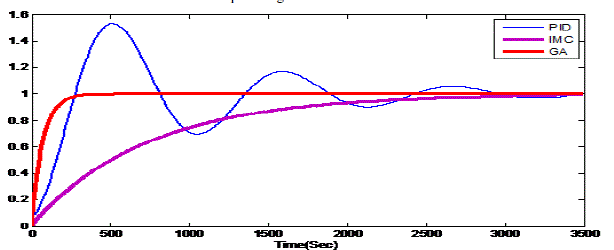
| It is clear from the responses that the GA based controller has the advantage of a better closed loop time constant, which enables the controller to act faster with a balanced overshoot and settling time. The response of IMC controller is more sluggish than the GA based controller. The time domain specification comparison is done for the IMC and GA based controllers for the responses obtained, is tabulated and given in Table 1. For the proposed model the comparison of performance index were done and are listed as per the given Table 2. |
CONCLUSION
|
| The various results presented above prove the better in their performances of the GA tuned PID settings than the PID controller Z-N II and IMC controller tuned ones. The simulation responses for the process models validated reflect the effectiveness of the GA based controller in terms of time domain specifications. The performance index under the various error criterions for the proposed controller is always less than the PID Z-N II and IMC tuned controller. Above all the simulated responses confirms the validity of the proposed GA based tuning for the temperature process. The closed-loop responses for Ziegler-Nichols II tuning for an ideal PID controller has offset and the responses are quite oscillatory[6]. This is one of the major disadvantages to the Z-N II tuning method. If the process conditions changes, then the control system may become oscillatory and unstable. In order to overcome these disadvantages advanced controllers like IMC control and GA controller are implemented. The main advantage of the IMC controller is, it provides a transparent framework for control system design and tuning [1] [7]. Thus, IMC is able to compensate for disturbances and model uncertainty. |
| The temperature control system is studied and the mathematical model of the first-order system with time delay (FOPDT) system is developed. Conventional PID and IMC controller is implemented for the system and the results are discussed [3]. The performance of GA controller is found to be good which ignores the presence of any Non linearity in the system [12] |
Tables at a glance
|
 |
 |
| Table 1 |
Table 2 |
|
Figures at a glance
|
 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
 |
 |
 |
 |
| Figure 6 |
Figure 7 |
Figure 8 |
Figure 9 |
|
References
|
- J.A.Arulandu, Braatz and Horn, I.G., C.J.Gombas, J.G.VanAntwerp and R.D.Braatz, “Improved Filter Design in Internal Model Control”Imd.Eng.Chem., 35 (10), 3437-3441.
- Chein, I.L. and P.S.Fruehauf, “IMC-Based PID controllers for “Real PID Control” Consider IMC Tuning to Improve Controller Performance”Chem.Eng.Prog.86(10), 33-41.
- European Journal of Scientific Research, Euro Journals Publishing, ISSN 1450-216X Vol.78 No.1. pp.65-73. 2012.
- DanlelE.Rlvera, Manfred Morarl, and SlgurdSkogestad Chemical Engineering, “Internal Model Control” 206-41.
- PID Controller Design” California Institute of Technology, Pasadena, California 9 1 125.
- M.Shamusuzzohal and Moonyong Lee “IMC Filter Design for PID Controller Tuning of Time Delayed Processes”.
- B.WayneBequette“Process Control Modeling, Design, and Simulation” by Prentice-Hall, Inc. 2003.
- E.Zafiriou, and Morari, M., Robust “A complete IMC design procedure Process Control, Prentice-Hall, Upper Saddle River, NJ.
- R. Oonsivilai and A. Oonsivilai ‘Gas Turbine Optimal PID Tuning by Genetic Algorithm using MSE’ World Academy of Science,Engineering and Technology.
- K.S. Tang, K.F. Man, S. Kwong and Q.HE “Genetic Algorithm and their Apllications”
- Pintu Chandra Shill, Md. Faijul Amin, M. A. H. Akhand, and Kazuyuki Murase Optimization of Interval Type-2 Fuzzy Logic ControllerUsing Quantum Genetic Algorithms WCCI 2012 IEEE World Congress on Computational Intelligence June, 10-15, 2012
- Sameh F. Desouky Howard M. Schwartz A Novel Technique to Design a Fuzzy Logic Controller Using Q learning and Genetic Algorithms inThe Pursuit-Evasion Game IEEE International Conference on Systems, Man, and Cybernetics San Antonio, TX, USA - October 2009
- S. Nithya, Abhay Singh Gour, N. Sivakumaran, T. K. Radhakrishnan and N. Anantharaman, Model Based Controller Design for Shell andTube Heat Exchanger, Sensors and Transducers Journal, Vol. 84, Issue 10, pp. 1677-1686, October 2007.
- D. Rathikarani, D. Sivakumar and S. Anita Janet Mary, Genetic algorithm based optimization of controller tuning for processes with deadtime, Proceedings of the International conference on Advances in control and optimization of dynamical systems(ACDOS), 2007.
- Gang-Wook Shin, Young-Joo Song, Tae-Bong Lee and Hong-Kyoo Choi, Genetic algorithm for identification of time delay systems from stepresponses, International Journal of Control, Automation, and Systems, Vol. 5, No. 1, Feb 2007, pp. 79-85.
- M. V. Sadasivarao and M. Chidambaram, PID controller tuning of cascade control systems using genetic algorithm, Journal of Indian Instituteof Science, 86, July-Aug 2006, pp. 343-354.
|