Keywords
|
| Conical Tank, PI Control, Level, MATLAB |
INTRODUCTION
|
| A basic problem in process industries is control of liquid level and flow in process tank. Conical tanks are extensively used in process industries, petrochemical industries, food process industries and wastewater treatment industries. Control of conical tank is a challenging problem because of its non-linearity and constantly changing in area of cross section. Hence for these reasons the conical tank process is taken here. Conventional PID controllers are simple, robust provided the system is linear. But the process considered here has nonlinear characteristics which is represented as piecewise linearized models.multiple linear models of tank with many PI controllers were implemented. Many researchers have been carried out in the level control of the conical tank process. S. M. Giri Raj kumar, K. Ramkumar, Sanjay Sharma [1] explained Ants colony optimisation in level control of conical tank. N.S. Bhuvaneswari , G. Uma , T.R. Rangaswamy[2] carried out experiments in conical tank level control using Neural Network controllers. Swati Mohanty[3 ] designed Model Predictive Controller for floatation column . Artificial Neural Network modeling and multivariable Model Predictive Controllers are designed by Rahul Shridhar, Douglas. J. Cooper [4]. Unconstrained multivariable Tuning was proposed by R. Shridhar, D. J. Cooper [5]. The detailed description of designing MPC is explained by E. F. Camacho, Carlos Bordons[6]. The softwares and technology offers the potential to implement more advanced control algorithms but in industries they prefer a robust and transparent process control structure that uses simple controllers. That is why the PID controller remains as the most widely implemented controller despite of the developments of control theory. |
| This paper endeavours to design a system using two methods process reaction curve method and skogestad method of obtaining PI values Process reaction curve method is also known as first method, we obtain experimentally the response of the plant to a unit-step input. If the plant involves neither integrator(s) nor dominant complex-conjugate poles, then such a unit step response curve may look S-shaped curve. Such step response curve may be generated experimentally or from a dynamic simulation of the plant. The S-shaped curve may be characterized by two constants, delay time L and time constant T. The PID tuner allows achieving a good balance between performance and robustness. The PID tuner considers the plant to be the combination of all blocks between the PID controller input and output. Thus, the plant includes all blocks in the control loop, other than the controller itself. |
| The method, which can be denoted skogestad method [7] after the originator, is based on the direct method. The control system tracking function T(s) is specified as a first order transfer function. The objective of this paper is to show that by employing the proposed tuning of PI controllers, an optimization can be achieved. This can be seen by comparing the result of the PI tuner by various methods. |
MODELLING AND SIMULATION
|
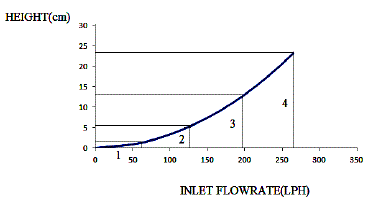
| Feedback control systems are often referred to as closed-loop control systems. In a closed-loop controlsystem the actuating error signal, which is the difference between the input signal and the feedbacksignal, is fed to the controller so as to reduce the error and bring the output of the system to a desiredvalue.The conical tank system, which exhibits the property of non-linearity, mathematical model is obtainedand simulated in SIMULINK. The process dynamics are analyzed in four segments so as toobtain effective models for the operating ranges. The operating ranges are concluded for 0-1.4 cm as model-1, 1.4-5.76 cm as model-2, 5.76-12.83 cm as model-3 and 12.83-23.04 cm as model-4. |
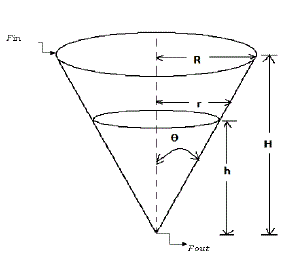
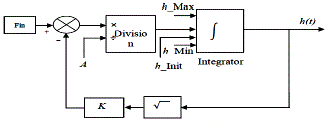
| The structure of conical tank system is illustrated in Fig 1. The tank level process to be simulated is single-input singleoutput (SISO) tank system as shown in Figure 2. The user can adjust the inlet flow by adjusting the control signal, Fin. During the simulation, the level „h’ will be calculated at any instant of time. In the SISO tank system, the liquid will flow into the tank through inlet and the liquid will come out from the tank through outlet. Here, we want to maintain the level of the liquid in the tank at desired value; so the measured output variable is the liquid level h.[8]. |
| A. Mathematical Modelling |
| The area of the conical tank is given by |
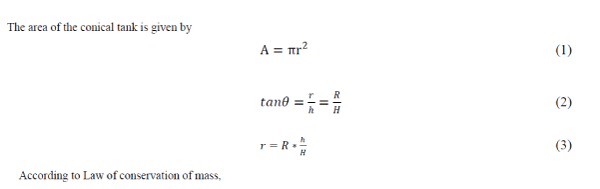 |
| Inflow rate - Outflow rate = Accumulation |
 |
PROBLEM FORMULATION
|
| A. Linearization |
| The process steady stateinput output characteristics thus obtained shows the non-linear behaviour as the area varies in a non-linear fashion with the process variable height (h).To obtain a linear model process steady state input – output characteristics curve is divided into five different linear regions as shown in the Figure 4. |
OPEN LOOP SYSTEM
|
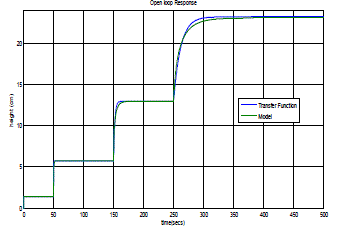
| The mathematical model is design in SIMULINK MATLAB and Open loop simulation results for step change in inlet flow rate is obtained. |
| The obtained response from open loop test which represents first order transfer function with zero dead time. |
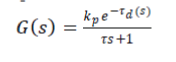 |
CONTROLLER DESIGN
|
| A. DIRECT SYNTHESIS METHOD |
| Direct Synthesis is a model based tuning technique. It uses an identified process model in conjunction with a user specified closed loop response characteristic.[9] This is a model based tuning technique. It uses an identified process model in conjunction with a user specified closed loop response characteristic. An advantage of this approach is that it provides insight into the role of the „modelâÃâ¬ÃŸ in control system design. |
| The overall transfer function for set point change assuming, |
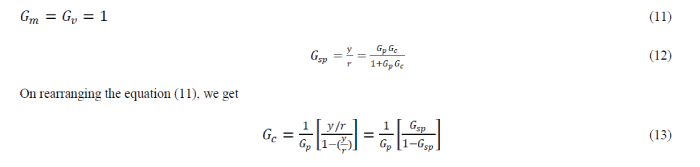 |
| Remarks on the direct synthesis method: |
| 1. It depends heavily on the model type. |
| 2. It requires model inversion, which may cause problem for non-minimum phase processes. |
| 3. PID controller may not be realized unless an appropriate model form is used to synthesis the control law. |
| B. SKOGESTAD METHOD |
| The method, which can be denoted skogestad method after the originator,is based on the direct method. The control system tracking function T(s) is specified as a first order transfer function. The objective of this paper is to show that by employing the proposed tuning of PI controllers, an optimization can be achieved. This can be seen by comparing the result of the PI tuner by various methods. |
SIMULATION RESULTS
|
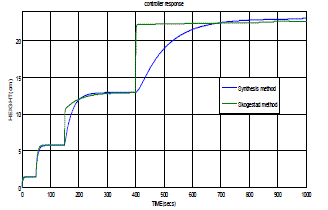
| The simulation result of Synthesis PI and skogestad with the various Operating point was obtained. The simulation was carried out in MATLAB Environment.The performance of the controller is compared [12] on the basis of Rise Time, Settling Time and Over Shoot. |
CONCLUSION
|
| An implementation of the PI controller is done bydirect synthesis method and skogestad method, the PI parameters obtained by process reaction curve method gives minimum rise time and quick settling time response. The tank level control is such a process which is perhaps more often used in all industrial processes including electrical, petroleum industry, power sectors, development sites, paper industry, beverages industry, etc. so the controlled stable operation of this drive attracts the researchers always, still keeping more and more future scope in it. |
Tables at a glance
|
 |
 |
 |
 |
| Table 1 |
Table 2 |
Table 3 |
Table 4 |
|
Figures at a glance
|
 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
|
References
|
- S. M. GiriRajkumar, Dr. K. Ramkumar, Sanjay Sarma O.V," Real time application of Ants Colony Optimization," International Journal of ComputerApplications (0975 - 8887) Vol 3 - No.8, June 2010.
- N.S. Bhuvaneswari , G. Uma , T.R. Rangaswamy," Adaptive and optimal control of a non-linear process using Intelligent controllers," Applied Soft Computing 9 , 182-190
- Swati Mohanty," Artificial neural network based system Identification and model predictive control of a flotation Column”, Journal of Process Control 19 (2009),pp 991-999
- Rahul Shridhar, Douglas J.Cooper," A Novel Tuning For Multivariable MPC",ISA Transactions,vol - 36,No.4,pp 273- 280.
- Rahul Shridhar , Douglas J.Cooper," A Tuning Strategy for Unconstrained Multivariable MPC", Ind. Eng. Chern. Res. 1998, 37, 4003-4016.
- E. F. Camacho, Carlos Bordons “Model Predictive Control”2nd edition, Springer.
- Skogested, S, “Simple analytic rules for model reduction and PID controller tuning”, Journal Process Control, 2003.
- S.Nithya, N.Sivakumaran, T.K.Radhakrishnan and N.Anantharaman” Soft Computing Based Controllers Implementation for Non-linear Process in Real Time” Proceedings of the World Congress on Engineering and Computer Science(WCECS )2010,Vol – 2.
- V.R.RaviT.Thyagarajan “Application of Adaptive Control Technique to Interacting Non Linear Systems “Electronics Computer Technology (ICECT),2011 3rd International Conference on8-10 April 20112 pp: 386 – 392.
- Sukanya R. Warier, SivanandamVenkatesh “Design of Controllers based on MPC for a Conical Tank System”IEEE-International Conference On Advances In Engineering, Science And Management (ICAESM -2012) March 30, 31, 2012.
- V.R.Ravi, T.Thyagarajan, M.MonikaDarshini“A Multiple Model Adaptive Control Strategy for Model Predictive controller for Interacting Non Linear Systems”International Conference on Process Automation, Control and Computing (PACC),July 2011.pp:1 – 8.
- R.Valarmathi, P.R.Theerthagiri, S.Rakeshkumar”Design and Analysis of Genetic Algorithm Based Controllers for Non Linear Liquid Tank System”IEEE-International Conference On Advances In Engineering, Science And Management (ICAESM -2012) March 30, 31, 2012.
|