Research & Reviews: Journal of Engineering and Technology
MenuISSN: 2319-9873
ISSN: 2319-9873
+44 7456 035580 Biya Motto Frederic*
Department of Physics, Faculty of Sciences, University of Yaoundé I, P O Box 812, Cameroon
Received: 10/07/2014; Revised: 22/07/2014; Accepted: 04/08/2014
Visit for more related articles at Research & Reviews: Journal of Engineering and Technology
The article contains the descriptions of fault-tree analysis as one of the methods of modelling the accidents and near misses in navigation. This method results in a quantitative evaluation of probability (frequency) of the potential hazardous event in fuzzy environment. Uncertainty of the initial data may be epistemic i.e. caused by expert judgement. It is proposed in the article to use the fuzzy numbers to describe the probabilities of the initial events of the accident scenario. The quantitative characteristics of the membership functions are determined by particular quantifier scale. The example of using the level sets method for evaluating the possibility of grounding the ship in the shallow waters is given
Risk, probability, grounding, fuzzy numbers, fault tree.
The security of maritime navigation is one of the most important problems of the navigation industry. International code for security management of ships exploitation and destruction of dirt and security management system, constructed on its basis regulates the activity of navigable companies in this area of activities.
According to regulations, the driving staff of the ship should be capable of evaluating the risk in various aspects of activity. Navigable companies are due to evaluate all the risks related to the ships, workers and environment and assure corresponding safety [8]. From the IMO guidelines [7], the term “risk” is defined as the combination of probability and weight for the consequences of unexpected events. For probability evaluation, the guidelines recommend the use of such logic methods as events tree and fault tree and also their combination [7].
In case of insufficient statistical data for probability evaluation of an unexpected event, it is recommended to use expert evaluation, physical analytic models and also imitation models.
Fuzzy subset A in the set U is called the couple in the form (u, μA(u)), where μA(u) is membership function (MF) of fuzzy subset. Normalized MF takes its values in the diapason [0,1]; U is called universal set and is composed of elements u, we note that uεU. MF μA(u) defines the degree of membership for any given element of subsetA to the set U.
Fuzzy numbers – they are fuzzy variables defined in real numbers axis R.
A fuzzy number is defined as a fuzzy subset A in the set R with MFμA (u)ε [1,0] and u ε R [2].
For example, a certain number u can be defined in the following form: {0/0.1;0.5/0.2; 1/0.3; 0.25/0.4; 0/0.5}
Where the denominator represents the membership degree of number u to a certain element of R axis:
Graphically, this will look as follows:
Depending on the source of non-determination of appearance, we distinguish types: random and epistemological. Random or statistical non-determination appears from real, unexpected variability in the behavior of studied system. Expert knowledge cannot reduce the given non-determination, but can serve to obtain its quantitative evaluation. For example, a boat passing through a canal will not always have the same trajectory (of movement) due to the fact that different external inputs are acting on the boat with sometimes unpredictable perturbations.
Figure 1: Graphic representation of fuzzy number u
Epistemological or systematic non-determination appears because of lack of practical knowledge from the expert about the system behavior and this is not acceptable. From psychological point of view this situation shows the possible mistakes in the expert’s knowledge. For example, an expert claims that the default probability of an electronic instrument is smaller than the one of mechanical but he is not totally sure of it.
From what is said above, sources of random non-determination can be the errors in measurements or empirical data, while epistemological non-determination is expert opinion and his estimates for future. For quantitative evaluation of an event’s frequency (probability) in a well defined time interval in case of expert evaluation, we use the quantifier scale method. An example of application is presented in table 1 [3].
Table 1: Scaling of quantifiers
For any scale order, we can introduce the following qualitative notion, related to the degree of expert certainty and determining the type of membership function (figure 2). In the horizontal axis, we represent p – probability (frequency) of not awaited event, expressed by a fuzzy number of the form {a/μ; b/μ; c/μ; d/μ}, and on vertical axis μ - degree of expert certitude in claiming the events probability.
Therefore, using a certain quantifier scale, with various forms of membership functions (MF), it is possible to create large class non-determination models of expert evaluations.
Figure 2: Types of MF depending on degree of expert certainty.
Methods of analyzing fault-tree (FT) and events-tree (ET) incorporate the methodology of operations on fuzzy numbers. Fault –tree is an organized graphic representation of conditions or other factors, provoking unexpected event, called summit of events [1]. In this paper, FT is understood as logic – probability model, whose elements are probabilities of unexpected event related to sea navigation security.
For accomplishment of the method of monotonous operations on fuzzy numbers, we form level sets. It is a further development of the principle of generalization and it consists of representing a fuzzy number as a group of convex fuzzy subsets of membership functions which either are strictly increasing, decreasing or constant.
If a continuous fuzzy number can be discretised in finite number of levels, then operations on fuzzy numbers will consist of operations on regions with equal monotony.are done on points abscises situated on the same level and in regions with the same monotony of corresponding functions.
Let us consider the method of level sets in the problem of probabilistic evaluation of multiplication of two events, of which their MF have trapezoid forms (figure 3).
Figure 3: MF of event probability
Membership function with trapezoid form can be interpreted as result of experts questionnaire, that present their discussions about probabilities as follows: probability of events 1 and 2 fall into the interval [a, d], but certain evaluation of probability belongs to the interval [b, c]. In table 2 are shown numerical parameters values a, b, c, d of membership function for each event.
Table 2: Parameters values of membership functions
For a better analysis of calculations results, we consider the number of discretisation levels k =4. Graphical explanation of membership function discretization is represented on figure 4 and table 2.
Figure 4: Discretisation of MF with levels number k =4.
In table 3 are shown examples of summit event probabilities in case when two events occur simultaneously (logic operation “AND” or multiplication) and when one of them occurs (logic operation “OR”, addition). We will use the same calculations for summit event probability in fault-tree.In the column “monotony” of table 3, we represent the character of membership of functions: “+” – increasing, “–” decreasing and “=” – constant.
Table 3: Initial data and results of logic operations “AND”, “OR” on fuzzy numbers.
Since discretisation level numbers for the values of event 1 and 2 have equal probabilities, then the results of actions on fuzzy numbers will also have the chosen discretisation level number (in our case it is 4). The levels of MF for each level is shown in column μ(pi). The argument values (probabilities) for each element is shown in columns p1 and p2.
Thus, we obtain evaluation of summit events probabilities, described by fuzzy numbers, depending on scenario “OR” (figure 5), “AND” (figure6).
Figure 5: Calculations results of evaluation of summit event probability with operation “OR” (disjunction).
Figure 6: Calculation results of evaluation of summit event probability with operation “AND”Conjunction
Let us consider the possible use of level sets method to analyse fault-tree shown on figure 7.
Figure 7: Fault-tree “probabilistic analysis of risk grounding ships in shallow water”
On figure 7 are used the following representations of initiator and summit events:
We assume that the initial information on probability of initiator events X1/X5 is gotten through analysis of experts evaluations and the possible occurrence of events is defined as a fuzzy set in the form of fuzzy number in the diapason [0,1] [5].
Table 3: Evaluations of probability initiation events X1/X5 by experts in the form of fuzzy numbers
If given probabilities Pi of events Xi, then the probability of summit event (“Grounding in shallow waters”) T is [4]:
PT (P1, P2, ---,P5) = P1P2 + (1 – P1P2)(P3+(1– P3)P4P5) eq1
The problem of evaluation summit event accomplishment is equivalent to determination of the following function.
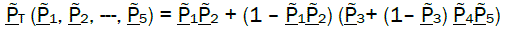
Where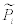 
– fuzzy number, which defines the probability of unexpected events.
We shall consider the number of discretisation levels k=10. When executing operations on fuzzy numbers similar to those done in paragraph 2 of our paper, we then obtain response in the form offuzzy number with MF that can be represented as a trapezium (figure 8).
Figure 8: Evaluation of probability of grounding the ship in shallow waters.
Membership functions for evaluation of grounding the ship in shallow water has trapezoidal form with the following parameters:
a = 11·10-3, b= 2.15·10-3, c = 2.46·10-3, d= 4.01·10-3.
Finally, the carrier of fuzzy set is the interval [a, d] = [1.1·10-3, 4.01·10-3].The nucleus of fuzzy set of obtained evaluation, i.e. a certain evaluation of probability value is the interval [b,c] = [2.15·10-3, 2.46·10-3].
Generally, we use the transformation from fuzzy form of MF to interval form by using variable values in the level μ = 0.5.
In this case the values interval of evaluation of the probability of grounding the ship in the shallow waters is [1.625·10-3, 3.231·10-3].
The choice of précised value depends on the character of problem to be solved.
The level sets method is a convenient and observable engineering instrument for evaluation and analysis of risk indicators when using fault-free method. The presentation of various forms of membership functions in expert evaluation and combination with quantifier scaling permits us to represent a large class of expert evaluations as fuzzy numbers. This gives a better risk evaluation in sea navigation.