Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Modelling, stability analysis and control of flexible single link robotic manipulator

Dinesh Singh Rana1, Deepika2
  1. Associate Professor, Department of Instrumentation, Kurukshetra University, Kurukshetra, India
  2. PG Student [Instrumentation Engineering], Dept. of Instrumentation, Kurukshetra University, Kurukshetra, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

In this paper, a mathematical model of flexible single link robotic manipulator that has a rotational base and translational motion has been developed using lagrangian method. The control strategies like PID, LQR and State feedback controller have been implemented for controlling the tip position of flexible single link robotic manipulators through MATLAB. State feedback controller uses pole placement approach, while the linear quadratic regulator (LQR) is obtained by resolving the Riccati equation. The best control strategy for controlling the tip position of flexible single link robotic manipulator is obtained by implementation of LQR controller. Finally, it is concluded from our study that LQR control method is the best method among PID and State feedback controller to control the flexible link manipulators.

Keywords
PID, LQR, MATLAB, State feedback controller.

INTRODUCTION
Robot and robot-like manipulators are now commonly employed, in hostile environment such as at various places in an atomic plant for handling radioactive materials, to construct and repair space stations and satellites [1-5]. Most of the robotic manipulators are designed and built in a manner to maximize stiffness in order to minimize the vibration of the end-effectors. Many industrial manipulators face the problem of arm vibrations during high speed motion. In order to improve industrial productivity, it is required to reduce the weight of the arms and to increase their speed of operation [5]. For these purposes, it is desirable to build flexible robotic manipulators that offer advantages of having less overall cost, larger work volume, high operational speed, smaller actuators, lower energy consumption, better transportability etc. Dynamics of flexible robotic manipulators are nonlinear. Nonlinear control is the area of control engineering specifically involved with systems that are nonlinear, time-variant, or both [4-6]. Nonlinear differential equations are used to describe the dynamic characteristics of nonlinear systems. The dynamics of nonlinear system can be linearized using classical and modern control theory and therefore able to characterize the nonlinear system [6-11].
The prime objective of this paper is to develop the mathematical model and control of flexible single link manipulators with help of control strategies such as PID, LQR and State feedback controller for controlling the tip position of flexible link manipulators through MATLAB [6]. State feedback controller uses pole placement approach, while the linear quadratic regulator is obtained by resolving the Riccati equation.

RESEARCH METHODOLOGY: MODELING OF FLEXIBLE LINK MANIPULATORS
The dynamic model of flexible manipulator involves modeling the rotational base and flexible link using Lagrange’s method. In order to determine the Lagrangian of system, we need to calculate Potential and Kinetic Energy. A lagrange function is defined as the difference between the total kinetic energy (K) and the total potential energy (P) of a mechanical system:
L = K-P
The dynamic model based on the lagrange formulation is obtained from the lagrangian, as a set of equations:
Where,
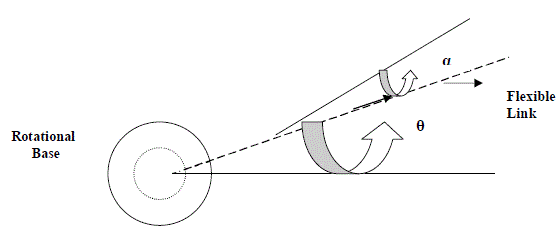
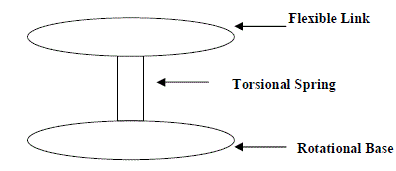
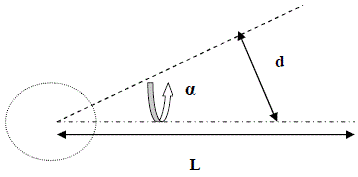
q is used as a joint variable which describes a linear displacement (d) for a prismatic joint and angular displacement (θ) for a rotary joint. The schematic of single link flexible manipulator is illustrated in figure 1 and its equivalent free body diagram has been illustrated in figure 2. The relationship between Length of flexible link(L), End point arc length deflection(d) and Arm Deflection (α ) has been illustrated in the figure 3. In present study the various parameters of single link flexible manipulator are tabulated in table 1.
Where, Ó¨ = Gear Angle (radians)
α = Arm Deflection (radians)
According to the definition of lagrange function, the lagrangian for single link flexible manipulator is given as:
The natural frequency of single link flexible manipulator is given by following equation:
α = d/L
Any frictional damping effects between the rotational base and flexible link are assumed negligible since the contact surface is fixed onto the base. We assume that θ and α are two generalized coordinates. We therefore have two equations:
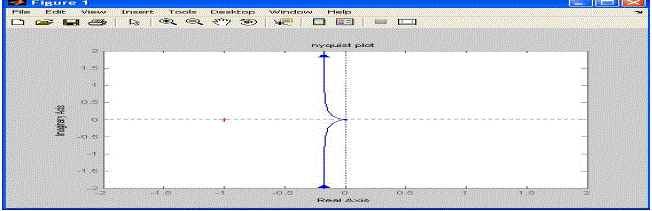
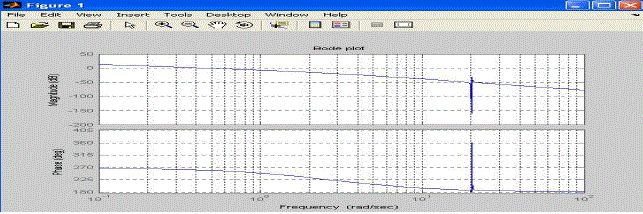
From the above analysis (figure 5) it is clear that the system is unstable, and to overcome these limitations, a controller is needed to design. The Bode plot in figure 6 shows discontinuity at frequency 20 rad/sec which represents the system is highly unstable. The magnitude as well as phase plots show monotonic decrease after 20 rad/sec frequency.
Controller Implementation of Flexible Link Manipulator: (i) PID Implementation:
The transfer function of single link flexible manipulator has been derived from its state space model i.e. using equation (16).
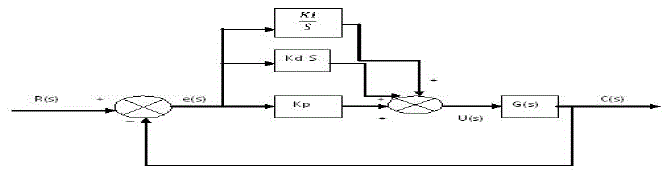
A controller compares the actual value of the plant output with the reference input, determines the deviation [13] and produces a control signal that will reduce the deviation to zero or to a small value. The PID controller implementation of flexible link manipulator has been shown in figure 7. The equation of a PID controller is given by-
Tuning of a PID involves the adjustment of Kp, Ki, and Kd to achieve some user defined "optimal" character of system response.
Where, Kp = Proportional Gain ; Kd = Derivative Gain; Ki = Integral Gain; R(s) = reference signal G(s) = Transfer Function of flexible link manipulator; e(s) = error signal; u(s) = plant input y(s) = output from the plant
Therefore, the open-loop transfer function of the diagram can be found as shown by the equation:
where G(s) is the plant transfer function.
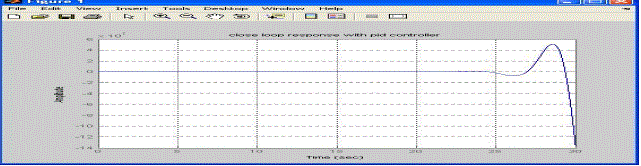
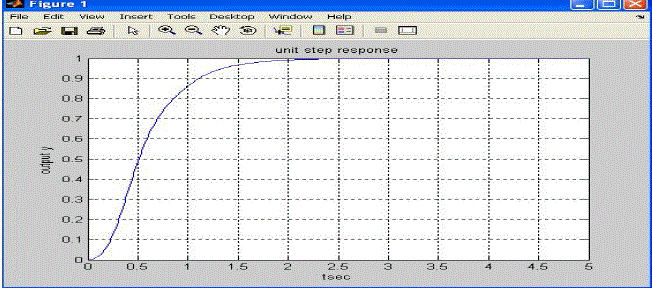
The open-loop transfer function in equation (22) can be implemented into MATLAB. The function polyadd is not originally in the Matlab toolbox [14-15]. It has to be copied to a new m-file to use it. This transfer function is assumed that both derivative and integral control will be needed along with proportional control. The actual control of this system could be stated by subjecting step input and its response which has been shown in figure 8.
(ii) State Feedback Controller design by pole placement approach
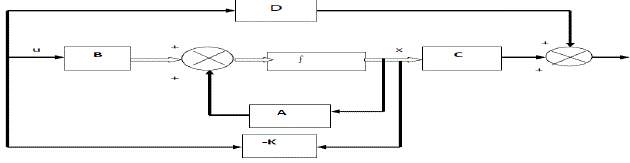
State –Feedback is the most important aspect of modern control system using an appropriate state-feedback, unstable system can be stabilized or damping oscillatory can be improved by pole placement design [13]. The performance of state feedback controller is depending upon pole positions and hence it becomes hit and trial procedure for controlling the flexible manipulators (single link). In designing a system using the pole placement approach several different sets of desired closed-loop poles need to be considered, the response characteristics compared, and the best one chosen.
Consider a control system
Where, x = state vector (n-vector), y = output signal (scalar)
u = control signal (scalar), A = n × n constant matrix
B = n × 1 constant matrix, C= 1 × n constant matrix
D = constant (scalar)
Let the control signal to be: U = -Kx (24)
This means that the control signal u is determined by an instantaneous state. Such a scheme is called state feedback. The (1 × n) matrix K is called the state feedback gain matrix. A block diagram for this system is shown in figure 9.
Substituting Equation (24) into equation (23) gives x(t) = (A-BK) x (t) . The solutions of this equation is given by
Where x(0) is the initial state caused by external disturbances. The stability and transient response characteristics are determined by the Eigen values of matrix A-BK. If matrix K is chosen properly, the matrix A-BK can be made an asymptotically stable matrix, and for x (0)≠0 , it is possible to make x (t) approach 0 as t approaches infinity. The eigen-values of matrix A-BK are called the regular poles. If these regulator poles are placed in the left-half s plane, then x (t) approaches 0 as t approaches infinity. The problem of placing the regular poles (closed-Loop poles) at the desired location is called a pole- place-placement problem.
Pole-placement problems can be solved easily with MATLAB. MATLAB has two commands- acker and place – for the computation of feedback gain matrix K. The command acker is based on Ackerman’s formula. This command applies to single-input system only [13]. The most commonly used commands are:
K= acker(A,B,J)
or, K= place(A,B,J)
where A and B are system matrices and J is a row vector containing the desired closed-loop poles. These commands returns the gain vector K.
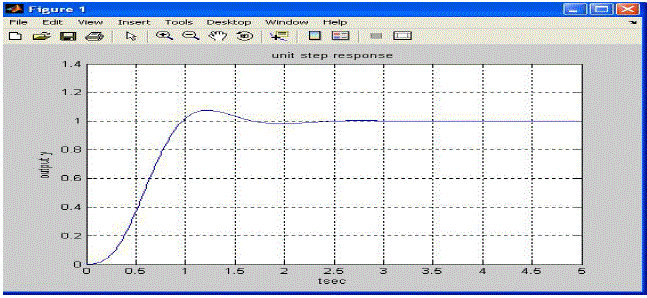
CASE 1: Choose the desired closed -loop poles at s=-2+j4, s=-2-j4, s=-10, s=-4
The feedback gain matrix K obtained [13] by these closed-loop pole is as follows:
K=[1.533 231.3162 -1.2551 -13.1102]
CASE 2
Choose the desired closed -loop poles at s=-4+j10, s=-4-j10, s=-3, s=-5
The feedback gain matrix K obtained by this closed-loop pole is as follows:
K= [3.3349 171.8775 -0.0898 -10.3945] and
CASE 3
Choose the desired closed –loop-poles at s=-3+5j, s=-3-5j,s=-2,s=-4
The feedback gain matrix K obtained by this closed-loop pole is as follows:
K=[0.5213, 259.76, -1.6155, -8.8193]
A unit step response of flexible link system using feedback gain matrix (Ko) from pole-placement method for case1, case2 and case3 are shown in figure 10, figure11 and figure12 respectively.

(iii) Linear Quadratic Regulator
The case where the system dynamics are described by a set of linear differential equations and the cost is described by a quadratic functional is called the LQ problem. One of the main results in the theory is that the solution is provided by the linear-quadratic regulator (LQR). In effect this algorithm therefore finds those controller settings that minimize the undesired deviations, like deviations from desired altitude [13]. Often the magnitude of the control action itself is included in this sum as to keep the energy expended by the control action itself limited. The LQR algorithm is, at its core, just an automated way of finding an appropriate state feedback controller.
Consider the optimal regulator given by system equation:
That determines the matrix K of optimal control vector
So as to minimize the performance index[13]
Where, Q and R is a positive definite or real symmetric matrix.
The block diagram showing the optimal configuration is shown in figure 13.Substituting equation (27) into (26), we obtain
x = Ax –BKx = (A-BK)x
Substituting equation (28) into (27), we obtain
Let us set x*(Q + K*RK)x = -d/dt (x*Px)
Where, P is positive definite Hermition-Matrix.
x*(Q + K*RK)x = -x*[(A-BK)*P + P (A-BK)]x
Comparing both sides of this equation and notice that this equation must hold true for any x, provided that
It can be proved that if A-BK is a stable matrix, there exist a [13] positive definite matrix that satisfies equation (29). The performance index J can be evaluated as
Since all eigen values of A-BK are assumed to have negative real parts, we have x(∞)---0.
Therefore, we obtain J=x*(0) Px(0) and hence, the performance index J can be obtained in terms of initial condition x(0) and P. To obtain the solution of quadratic optimal control problem, we proceed as : R = T*T , where, T is a nonsingular matrix. Then equation (29) can be written as (A*-K*B*)P + P(A-BK) + Q + K*T*TK = 0.
The minimization of J w.r.t. K requires the minimization of
x*[TK-(T*)-1 B*P]*[TK-(T*)-1B*P]x w.r.t. K
The minimum occurs when it is zero or when TK = (T*)-1B*P and
Equation (29) gives the optimal matrix K. Thus, the optimal control law to the quadratic optimal control problem, when the performance index is given by equation (28) is linear and is given by u(t) = -Kx(t) = R-1B*Px(t)
The matrix P in equation (31) must satisfy equation (29) or the following reduced equation:
Equation (32) is called the reduced matrix Riccati equation. The design steps may be stated as follows:
(i) solve equation (32), the reduced matrix Riccati equation for matrix P.
(ii) Substitute this matrix P into equation (31). The resulting matrix K is the optimal matrix.
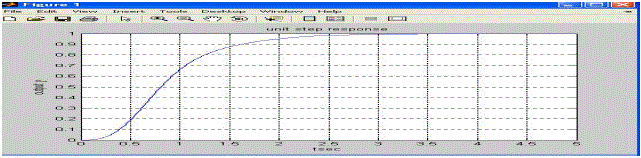
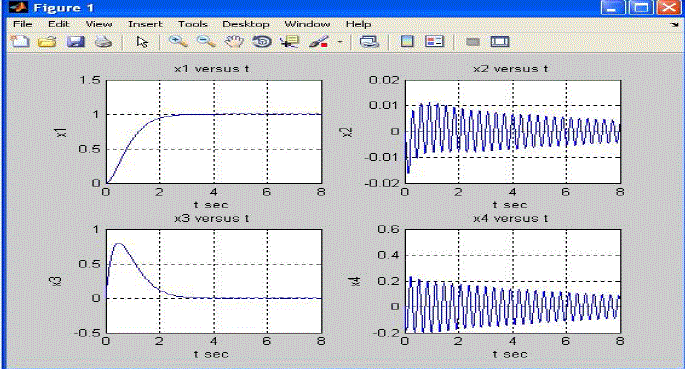
The Unit step response of double link flexible manipulator using LQR method is illustrated in figure14. Figure 14 shows that the gear angle is settle to the set point very quickly without any overshoot .
Where x1 corresponds to θ (gear angle), x2 corresponds to α(arm deflection)

CONCLUSIONS
In this paper, the various aspects on mathematical modelling and control strategies of flexible link manipulators have been investigated. A mathematical model of flexible link manipulators i.e. single link has been developed using lagrangian method. These mathematical models have been characterized using classical and modern control theories. Their time domain and frequency domain analysis has been carried out and our study show that the mathematical models of flexible manipulators are highly unstable systems. Different control strategies such as PID, LQR and State feedback controller have been implemented for controlling the tip position of flexible manipulators (single link). It was concluded from our results of implementation of various controllers for flexible link manipulators problem that the state feedback and linear quadratic regulator (LQR) controller providing the better performance than conventional PID controllers.

Tables at a glance
Table icon
Table 1
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 6 Figure 7 Figure 8 Figure 9 Figure 10
Figure 1 Figure 2 Figure 3 Figure 4
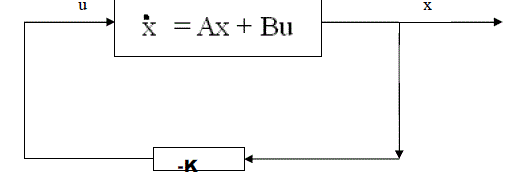Figure 11 Figure 12 Figure 13 Figure 14
 

References