Keywords
|
| Image denoising, Image classification, Adaptive multi resolution, mean square error estimation, Image restoration and decomposition. |
INTRODUCTION
|
| Research and Technology field requires the application of Image Processing Schemes. Digital images are very important in the areas of geographical information systems and astronomy. Satellite television magnetic resonance Imaging, computer tomography is some of the daily life applications wherein digital images play a vital role. All natural phenomena and transmission errors are degrading the image quality thereby noise is introduced in the image. Hence there is a need for image denoising procedure to reduce the noise level present in the image so as to produce the denoised image closer to the original image. |
EFFICIENT DENOISING PROCEDURES
|
| A system which introduces the linear minimum mean square error estimation framework proposed by Zhang L, Li X, Zhang D [1] for image denoising promises good image outputs. Image Acquisition process, Noise is introduced into the system. The denoised image is used for image interpolation. Image fine and edge structure may be spoiled due to image denoising thereby producing artifacts. A directional denoising algorithm is proposed which uses directional interpolator. The noiseless and missing samples are estimated for similar framework with optimal estimation. The estimation process is calculated by collective effort of adaptive calculation of local statistics. A more accurate output is obtained by combining various directional estimates computed in multiple directions. The missing sample interpolation uses the estimation parameters which are evaluated from the denoising process. This method reduces interpolation artifacts caused by the noise and the image edge structures are preserved well. |
| Two Complementary discontinuity measures are used in the proposed novel Bayesian image denoising algorithm [2].Due to the over-locality characteristics of spatial discontinuity, the significant discontinuities cannot be detected from noisy image. But the spatial discontinuity effectively preserves the edge image components. Hence there is an additional requirement on finding new discontinuity measure for feature preservation by detecting contextual discontinuities. The availability of degree of uniformity in small regions and the effective detection of significant discontinuities are the primary advantages of the local-in homogeneity measure proposed in this scheme. The prior probabilities of Bayesian denoising framework are created by employing the combined complementary discontinuity measures. This achieves high peak signal to noise ratio, reduction in noise effectively by edge components preservation. |
IMAGE DENOISING ALGORITHMS
|
| Three scales of dual tree complex wavelet coefficients are used for image denoising algorithm for removal of white Gaussian noise. The approximate shift invariance and the better directional selectivity are the two important features of dual tree complex wavelet transform. Chen G, Zhu W.P and Xie W [3] have proved that it is providing highly competitive outputs. |
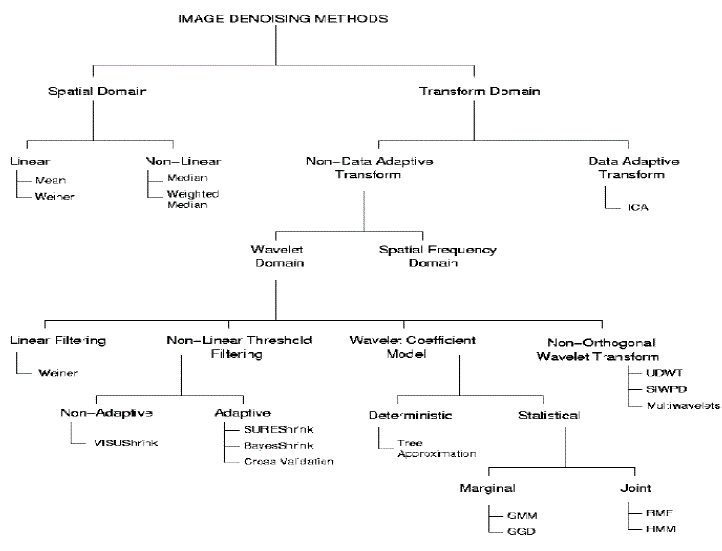
| For three Dimensional magnetic resonance images, an innovative method is proposed [4] based on block wise non-local (NL)-means with adaptive multi resolution. With respect to the spatial and frequency contents present in the image, the amount of denoising is implicitly adapted in accordance with the adaptive soft wavelet coefficient mixing. Fig.1 shows the types of various image denoising procedures |
| The filter is applicable for both Gaussian noise and Rician noise .Compared to the latest technique called Rician NL means filter, this method (multi resolution filter) achieves highly competitive measures in the quantitative validation conducted using several quality metrices on Brain web datasets. The filter removes noise efficiently by preserving fine details in noisy and classical cases by conducting qualitative experiments on various images like anatomical and diffusion weighted MR images. This is applied in the field of fibre tracking. |
| For removal of random valued impulse noise, authors [5] have proposed an improved decision based detail preserving variational method. In highly corrupted images, it is necessary to improve the ability of detection. To obtain this, variable window technique is employed by adaptive centre weighted median filter. The difference noise marks are labeled with classification of noisy parts of the image by fast iteration strategy performed by improved ACWMF. A weight adjustable detail-preserving variational method is applied for restoring all the noisy parts as one time event. The noise marks decides the weights of DPVM’s convex cost function between data fidelity term and smooth regularization term. The restored image is retrieved after minimization. The version and quantitative measurements done by the proposed filter, outperforms all other existing algorithms. It is very faster and can be ported into practical and real time applications easily. |
| The following chart describes the comparison between the noise removing technologies applied for different kind of noises like impulse noise, Gaussian noise, Rician noise and speckle noise. Several noise models are discussed corresponding to their type of images like real, Synthetic, Satellite and Ultrasound images. decomposition is presented in the form of new model. A non- convex, non-smooth regularization and Hilter Sobolev spaces of negative degree of differentiability [6] are applied in the new algorithm. This is capturing oscillatory patterns. |
| A proven pseudo solution is existing for the proposed model. Also the variable splitting and penalty techniques are used to solve the minimization problem by two different numerical algorithms. Various experiments are also conducted for image denoising, deblurring and decomposition for real and synthetic images. |
| With the statistical modeling of wavelet coefficients, the speckle noise is suppressed for ultrasound images. A two dimensional heteroscedasticity will be existing between the significant non-Gaussian statistics of log transformed ultrasound image which are categorized based on wavelet coefficients. Two dimensional GARCH [7] -2D. |
DISCUSSION
|
| All existing efficient denoising procedures are discussed and the various performance metrices are categorized. In all the types of denoising algorithms, the components used and the applications are also listed. Since every individual algorithm possesses its own merits and merits , it is suggested that two or more efficient techniques may be combined together to receive the desired results. A relevant algorithm is to be identified in such a way that it is providing the advantages of both the systems which are combined. |
Tables at a glance
|
 |
| Table 1 |
|
| |
Figures at a glance
|
 |
| Figure 1 |
|
| |
References
|
- Zhang L,Li X and Zhang D, “Image Denoising and Zooming under the linear minimum mean square error estimation framework”, ImageProcessing IET,Vol6,Issue 3, pp.273-283,April 2012.
- Jung C,Jiao L.C and Gong M.G., “Bayesian Image Denoising using two Complementary discontinuity measures”,Image Processing IET, Vol. 6, Issue 7, pp.932-942, October 2012.
- Chen G,Zhu W.P and Xie W, “Wavelet based Image Denoising using three scales of dependencies ”, Image Processing IET, Vol.6, Issue 6, pp.756-760, August 2012.
- Coupe P, Manjon J.V., Robles M and Collins D.L.,”Adaptive multi resolution non-local means filter for three dimensional magnetic resonance image denosing”, Image Processing IET, Vol.6, Issue 5, pp.558-568.
- Zhou, Y.Y, Ye.Z.F. and Huang.J.J,”Improved decision based detail preserving Variational method for removal of random valued impulse noise”, Image Processing IET, Vol.6, Issue 7, pp.976-985.
- Lu.C.W,”Image Restoration and Decomposition using non convex non-smooth regularization and negative Hilbert-Sobolev norm”, Image Processing IET,Vol.6, Issue 6, pp.706-716.
- Amirmazaghani M and Amindayar H,” Wavelet Domain Processor “Image Processing IET, Vol.6, Issue 5, pp.580-588.
|