Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Modified Differential Evolution Algorithm for Economic Load Dispatch Problem with Valve- Point Effects

Hardiansyah1
Department of Electrical Engineering, Tanjungpura University, Pontianak, Indonesia1
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

This paper presents a new approach for solving of the economic load dispatch (ELD) problem with valve-point effects using a modified differential evolution (MDE) algorithm. The practical ELD problems have nonsmooth cost function with equality and inequality constraints, which make the problem of finding the global optimum difficult when using any mathematical approaches. The modifications of improved DE by considering the following factors: (1) the scaling factor F, (2) selection scheme, (3) an auxiliary set, and (4) treatment of constraints. To demonstrate the effectiveness of the proposed approach, the numerical studies have been performed for two different test systems, i.e. six and fifteen generating unit systems, respectively. The results shows that performance of the proposed approach reveal the efficiently and robustness when compared results of other optimization algorithms reported in literature.

Keywords
Differential evolution, economic load dispatch, non-smooth cost functions, valve-point effects.

INTRODUCTION
Power utilities are expected to generate power at a minimum cost. The generated power has to meet the load demand and transmission losses. ELD problem is considered to be one of the key functions in electric power system operation. Also, for the secure operation of the power system, the generator should be dispatched, so that the transmission capacity limits are not exceeded. ELD problem is one of the fundamental issues in power system operation. In essence, it is an optimization problem and its objective is to reduce the total generation cost of units, while satisfying constraints.
Several classical optimization techniques such as lambda iteration method, gradient method, Newton’s method, linear programming, Interior point method and dynamic programming have been used to solve the basic economic dispatch problem [1]. These mathematical methods require incremental or marginal fuel cost curves which should be monotonically increasing to find global optimal solution. In reality, however, the input-output characteristics of generating units are non-convex due to valve-point loadings and multi-fuel effects, etc. Also there are various practical limitations in operation and control such as ramp rate limits and prohibited operating zones, etc. Therefore, the practical ELD problem is represented as a non-convex optimization problem with equality and inequality constraints, which cannot be solved by the traditional mathematical methods. Dynamic programming method [2] can solve such types of problems, but it suffers from so-called the curse of dimensionality. Over the past few decades, as an alternative to the conventional mathematical approaches, many salient methods have been developed for ELD problem such as genetic algorithm (GA) [3], improved tabu search (TS) [4], simulated annealing (SA) [5], neural network (NN) [6], evolutionary programming (EP) [7, 8], particle swarm optimization (PSO) [9-11], and biogeography algorithm (BGA) [12].
Differential evolution (DE) algorithm introduced by Storn and Price in 1995, belongs to the group of evolutionary algorithms which operate in continuous search spaces [13, 14]. DE has been successfully applied to many problem domains such as: economic dispatch [15, 16], short-term scheduling [17], power system planning [18, 19], etc. This algorithm has high efficiency for solving continuous nonlinear optimization problems and multimodal environments. The advantages of the DE are simple structure, a few control parameters and high reliable convergences. The DE is one type of modern optimization techniques, which based on a population searching mechanism like as GA [3], artificial bee colony (ABC) optimization [20] and PSO [9-11].
In this paper, a novel approach is proposed to solve the ELD problem with valve-point effects using a modified differential evolution (MDE) algorithm. The proposed method considers the nonlinear characteristics of a generator such as valve-point effects and transmission losses. Feasibility of the proposed MDE method has been demonstrated on two different test systems, i.e. six and fifteen generating unit systems. Results obtained show that the proposed approach can obtain more optimum solutions.

ECONOMIC LOAD DISPATCH FORMULATION

2.1. Economic load dispatch (ELD) problem
The objective of an ELD problem is to find the optimal combination of power generations that minimizes the total generation cost while satisfying equality and inequality constraints. The fuel cost curve for any unit is assumed to be approximated by segments of quadratic functions of the active power output of the generator. For a given power system network, the problem may be described as optimization (minimization) of total fuel cost as defined by (1) under a set of operating constraints.
Where T F is total fuel cost of generation in the system ($/hr), ai, bi, and ci are the cost coefficient of the i th generator, Pi is the power generated by the i th unit and n is the number of generators.
The cost is minimized subjected to the following constraints:
Power balance constraint,
Generation capacity constraint,
where Pi, min and Pi, max are the minimum and maximum power output of the i th unit, respectively. PD is the total load demand and PLoss is total transmission losses. The transmission losses PLoss can be calculated by using B matrix technique and is defined by (4) as,
where Bij is coefficient of transmission losses.

2.2. ELD problem considering valve-point effects
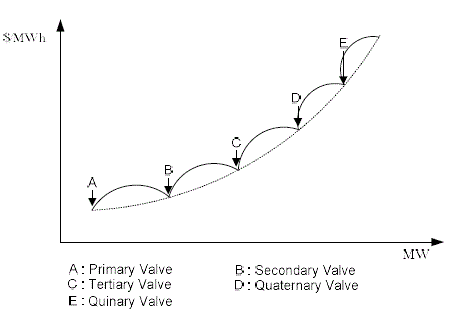
For more rational and precise modeling of fuel cost function, the above expression of cost function is to be modified suitably. The generating units with multi-valve steam turbines exhibit a greater variation in the fuel cost functions [10]. The valve opening process of multi-valve steam turbines produces a ripple-like effect in the heat rate curve of the generators. These “valve-point effects” are illustrated in Fig. 1.
The significance of this effect is that the actual cost curve function of a large steam plant is not continuous but more important it is non-linear. The valve-point effects are taken into consideration in the ELD problem by superimposing the basic quadratic fuel-cost characteristics with the rectified sinusoid component as follows:
where FT is total fuel cost of generation in ($/hr) including valve point loading, ei, fi are fuel cost coefficients of the i th generating unit reflecting valve-point effects.

DIFFERENTIAL EVOLUTION (DE) ALGORITHM
Differential evolution (DE) developed by Storn and Price [13] is a population based evolutionary computation technique, capable of handling non-differentiable, non-linear and multi-modal objective functions. Due to its simple but powerful and straightforward features, it is very attractive for resolving the non-convex global optimization problems. In DE, the fitness of an offspring competes one-to-one with that of the corresponding parent. This one-to-one competition will give rise to a faster convergence rate than other EAs. In addition, only a few control parameters are required in comparison with other computing heuristic optimization methods [14]. The basic algorithm of DE typically consists of four phases: 1) initialization, 2) mutation, 3) crossover, and 4) selection phases. The mutation and crossover are used to generate new individuals, and the selection then determines that the individuals will survive into the next generation. The performance of DE algorithm usually depends on three parameters, i.e., population size NP, mutation factor MF, and crossover rate CR [13, 14].
A brief description of different steps of DE algorithm is given below:

3.1. Initialization
The population is initialized by randomly generating individuals within the boundary constraints
where 0 ij X is the initialized jth decision variable of ith population set; ‘rand’ function generates random values uniformly in the interval [0, 1]; Np is the size of the population; D is the number of decision variables. The fitness function is evaluated for each individual. min j X and max j X are the lower and upper bound of the jth decision variable, respectively.

3.2. Mutation
As a step of generating offspring, the operations of ‘mutation’ are applied. ‘Mutation’ occupies quite an important role in the reproduction cycle. The mutation operation creates mutant vectors k i X ' by perturbing a randomly selected vector k a X with the difference of two other randomly selected vectors k b X and k c X at kth iteration as per following equation.

MODIFIED DIFFERENTIAL EVOLUTION
This section presents the modifications to the simple DE method that lead to a modified differential evolution (MDE) algorithm.

4.1. Scaling factor F
In the initial DE, the scaling factor F in (7) is constant during the optimization process and F takes values in the range [0, 2]. However, no optimal choice of F has been proposed in the bibliography for DE. All the studies used an empirically derived value, and in most cases F varies from 0.4 to 1. This means F is strongly problemdependent and the user should choose F carefully after some trial and error tests. In this section, F is varied randomly within some specified range, as follows:
where a and b are positive and real-valued constants, the sum of a and b is less than 1, randi [0, 1] denotes a uniformly distributed random value in the range [0, 1].
Consequently, F is different for each generation, and the computation of F by (10) is effective when the optimal value of F is difficult to be determined for complicated problems like ELD.

4.2. Selection scheme
In the original DE, the trial vector or offspring k i X " is compared with the target vector k i X , whose index is the same as the running index i, using (9). In the modified DE algorithm, the trial vector is compared with the nearest target vector in the sense of Euclidean distance. This comparison scheme is employed in the crowding DE algorithm for multimodal function optimization. By this scheme, as the optimization proceeds, the individuals are scattered and gathered around the local optimal points. However, in this section, only global optimization is considered, and if there is no improvement of the optimal value during a predefined number of generations, then the comparison scheme is changed to that of the original DE.
Therefore, in the initial period of optimization, the DE algorithm explores to find not only global but also local optima, and in the later stage, it searches only for the global optima with greedy selection scheme.

4.3. Auxiliary set
In the selection of the next generation individual, if the trial vector is worse than the target vector, then the trial vector is discarded. To enhance the explorative search and the diversity of the population, an auxiliary set is employed. The auxiliary set Pa has the same population size NP, and the initialization process is the same as that of the main set, using (6). At each generation, if the trial vector k i X " when compared with the corresponding target vector in the main set is found to be worse than its target vector, then the rejected trial vector is compared with the point k i Z with the same running index i in the auxiliary set Pa. If
To use the solutions in Pa, after a predefined number of generations, several of the worst solutions in the main set are periodically replaced with the best ones in the auxiliary set by comparing the objective function value.

4.4. Treatment of constraints
Most optimization problems in the real world have constraints to be satisfied. One common approach to deal with constraints is to penalize constraint violations using an appropriate penalty function. In this approach, considerable effort is required to tune the penalty coefficients. In this section, three selection criteria are used to handle the constraints of the ELD problem:
1. If two solutions are in the feasible region, then the one with the better fitness value is selected.
2. If one solution is feasible and the other is infeasible, then the feasible one is selected.
3. If both solutions are infeasible, then the one with the lowest amount of constraint violation is selected.
It should be noted that the final (best) solution provided by MDE is accepted only if it is feasible; otherwise, the execution of MDE algorithm is repeated.

4.5. Handling of integer variables
DE in its initial form is a continuous variables optimization algorithm, and was extended to mixed variables problems. During the evolution process, the integer variable is treated as a real variable, and in evaluating the objective function, the real value is transformed to the nearest integer value as follows:
where,
where INT (xj) function gives the nearest integer to xj, and the solution vector is x=[x1,x2,,,,,,,xD].

SIMULATION RESULTS
To verify the feasibility and performance efficiency of applying MDE algorithm to solve ELD with taking the effect of valve ripples into consideration, several cases were tested and investigated. Among of these, two cases will be presented. The proposed MDE algorithm is applied to solve both the six-unit and fifteen-unit system with considering valve-point effects and transmission losses.
Test Case 1: 6-unit system
The system consists of six thermal generating units with valve point effects. The total load demand on the system is 1263 MW. The parameters of all thermal units are presented in Table 1 [9].
The transmission losses are calculated by B matrix loss formula which for 6-unit system is given as:
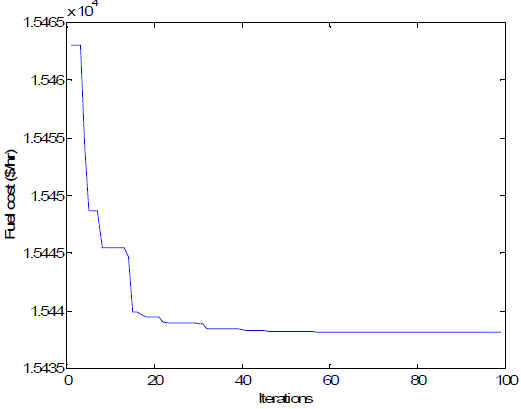
The obtained results for the 6-unit system using the MDE method are given in Table 2 and the results are compared with other methods reported in literature, including GA, PSO, PSO-LRS, NPSO, and NPSO-LRS [11]. It can be observed that MDE can get the total generation cost of 15,438 ($/hr) and power losses of 11.9069 (MW), which is the best solution among all the methods. Note that the outputs of the generators are all within the generator’s permissible output limit. A convergence characteristic of six-generator system is shown in Fig. 2.
Test Case 2: 15-unit system
This system consists of 15 generating units and the input data of 15-generator system are given in Table 3 [9]. Transmission loss B-coefficients are taken from [21]. In order to validate the proposed MDE method, it is tested with 15-unit system having non-convex solution spaces, and the load demand is 2630 MW.
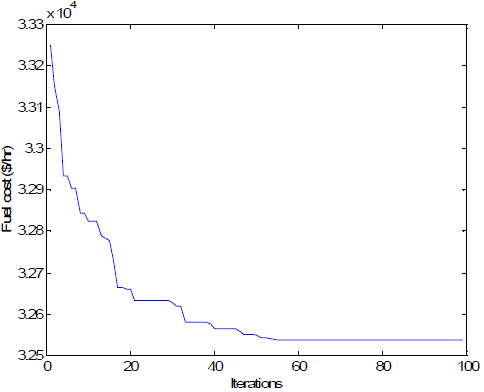
The best fuel cost result obtained from proposed MDE and other optimization algorithms are compared in Table 4 for load demands of 2630 MW. In Table 4, generation outputs and corresponding fuel cost and losses obtained by the proposed MDE are compared with those of GA, and PSO [21]. The proposed MDE provide better solution (total generation cost of 32,537 $/hr and power losses of 30.3477 MW) than other methods while satisfying the system constraints. We have also observed that the solutions by MDE always are satisfied with the equality and inequality constraints by using the proposed constraint-handling approach. A convergence characteristic of fifteen-generator system is shown in Fig. 3.

CONCLUSION
In this paper, a modified differential evolution (MDE) algorithm has been proposed, developed, and successfully applied to solve ELD problem with valve-point effects. The ELD problem has been formulated as a constrained optimization problem where an objective function has been considered to minimize the total generation cost. The proposed approach has been tested and examined on two different test systems. The simulation results demonstrate the effectiveness and robustness of the proposed algorithm to solve ELD problem. Moreover, the results of the proposed MDE algorithm have been compared to those reported in the literature. The comparison confirms the effectiveness and the superiority of the proposed MDE approach over the heuristic techniques in terms of solution quality.

Tables at a glance
Table icon Table icon Table icon Table icon
Table 1 Table 2 Table 3 Table 4
 

Figures at a glance
Figure 1 Figure 2 Figure 3
Figure 1 Figure 2 Figure 3
 

References