Keywords
|
| Clustering analysis, K-means algorithm, distance, computational complexity |
INTRODUCTION
|
| Clustering is a way that classifies the raw data reasonably and searches the hidden patterns that may exist in datasets. It is a process of grouping data objects into disjointed clusters so that the data in the same cluster are similar, yet data belonging to different cluster differ.The demand for organizing the sharp increasing data and learning valuable information from data, which makes clustering techniques are widely applied in many application areas such as artificial intelligence, biology, customer relationship management,data compression, data mining, information retrieval, image processing, machine learning, marketing, medicine, pattern recognition, psychology, statistics and so on. |
| K-means is a numerical, unsupervised, non deterministic, iterative method. It is simple and very fast, so in many practical applications, the method is proved to be a very effective way that can produce good clustering results. But it is very suitable for producing globular clusters. The k-means algorithm is effective in producing clusters for many practical applications in emerging areas like Bioinformatics . But the computational complexity of the original kmeans algorithm is very high. Moreover, this algorithm results in different types of clusters depending on the random choice of initial centroids. This paper deals with a heuristic method based on sorting and partitioning the input data for finding better initial centroids, thereby improving the accuracy of the kmeans algorithm. |
THE K-MEANS CLUSTERING ALGORITHM
|
Existing K-means algorithm
|
| In existing system,K-means algorithm proceeds it randomly select k of the objects,each of which initially represents a cluster mean or center. For each of the remaining objects, an object is assigned to the cluster to which it is the most similar,based on the distance between the object and the cluster mean. It then computes the new mean for each cluster. This process iterates the criterion function converges. |
| K-means is a typical clustering algorithm in data mining and which is widely used for clustering large set of data. In 1967, MacQueen firstly proposed the K-means algorithm; it was one of the most simple, non-supervised learning algorithms, which was applied to solve the problem of the well-known cluster. It is a partitioning clustering algorithm, this method is to classify the given date objects into k different clusters through the iterative, converging to a local minimum. So the results of generated clusters are compact and independent. The algorithm consists of two separate phases. The first phase selects k centers randomly, where the value k is fixed in advance. The next phase is to take each data object to the nearest center. Euclidean distance is generally considered to determine the distance between each data object and the cluster centers. When all the data objects are included in some clusters, the first step is completed and an early grouping is done. Recalculating the average of the early formed clusters. This iterative process continues repeatedly until the criterion function becomes the minimum. Supposing that the target object is x, xi indicates the average of cluster Ci, criterion function is defined as follows: |
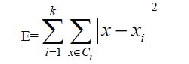 |
| E is the sum of the squared error of all objects in database.The distance of criterion function is Euclidean distance, which isused for determining the nearest distance between each data objects and cluster center. The Euclidean distance between onevector x=(x1 ,x2 ,…xn) and another vector y=(y1 ,y2 ,…yn ), The Euclidean distance can be obtained as follow: |
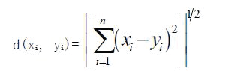 |
| The process of K-means algorithm as follow: |
| Input: |
| Number of desired clusters, k, and a database D={d1, d2,…dn} containing n data objects. |
| Output: |
| A set of k clusters |
| Steps: |
| 1. Randomly select k data objects from dataset D as initial cluster centers. |
| 2. Repeat; |
| 3. Calculate the distance between each data object di (1 <= i<=n) and all k cluster centers cj(1<=j<=k) and assign data object di to the nearest cluster. |
| 4. For each cluster j (1<=j<=k), recalculate the cluster center. |
| 5. until no changing in the center of clusters. |
| The K-means clustering algorithm always converges to local minimum. Before the K-means algorithm converges, calculations of distance and cluster centers are done while loops are executed a number of times, where the positive integer t is known as the number of K-means iterations. The precise value of t varies depending on the initial starting cluster centers . |
| The distribution of data points has a relationship with the new clustering center, so the computational time complexity of the K-means algorithm is O(nkt). n is the number of all data objects, k is the number of clusters, t is the iterations of algorithm. Usually requiring k <<n and t <<n. |
PROPOSED SYSTEM
|
| The k-means clustering algorithm consists of two separate phases: the first phase is to define k centroids, one for each cluster. The next phase is to take each point belonging to the given data set and associate it to the nearest centroid. When all the points are included in some clusters, the first phase is completed and an early grouping is done. At this point we need to recalculate the new centroids, as the inclusion of new points may lead to a change in the cluster centroids. Once we find k new centroids, a new binding is to be created between the same data points and the nearest new centroid, generating a loop. As a result of this loop, the k centroids may change their position in a step by step manner. Eventually, a situation will be reached where the centroids do not move anymore. |
Algorithm
|
Input:
|
| D = {d1, d2,......,dn} // set of n data items. |
| k // Number of desired clusters. |
Output:
|
| A set of k clusters. |
Steps:
|
| 1. For each column of the data set, determine the range as the difference between the maximum and the minimum element; |
| 2. Identify the column having the maximum range; |
| 3. Sort the entire data set in non-decreasing order based on the column having the maximum range; |
| 4. Partition the sorted data set into ‘k’ equal parts; |
| 5. Determine the arithmetic mean of each part obtained in Step 4 as c1, c2,….ck; Take these mean values as the initial centroids. |
6. Repeat
|
| 6.2 Assign each data item di to the cluster which has the closest centroid; |
| 6.3 Calculate new mean of each cluster; |
| Until convergence criterion is met. |
EXPERIMENTAL RESULTS
|
| The original k-means and the enhanced k-means algorithms require the values of the initial centroids also as input, apart from the input data values and the value of k. The experiment is conducted for different sets of values of the initial centroids, which are selected randomly. For the proposed algorithm, the data values and the value of k are the only inputs required. The accuracy of clustering is determined by comparing the clusters obtained by the experiments with the pre-determined clusters already available in the UCI data set. The percentage accuracy and the time taken for each experiment are computed and tabulated. |
 |
CONCLUSION
|
| K-means is a typical clustering algorithm and it is widely used for clustering large sets of data.Our project elaborates K-means algorithm and analyses the shortcomings of the standard K-means clustering algorithm. Because the computational complexity of the standard K-means algorithm is objectionably high owing to the need to reassign the data points a number of times during every iteration, which makes the efficiency of standard K-means clustering is not high. Our project presents a simple and efficient way for assigning data points to clusters. The proposed method in our project ensures the entire process of clustering in O(nk) time without sacrificing the accuracy of clusters. |
References
|
- Liang Wang,XinGeng,JamesBezdek,ChristopherLekie,KotagiriRamamohanarao ”Automatically Determining Number of clusters in Unlabeled Dataset” IEEE Transaction on Knowledge Engineering Vol.21 No.3 March 2009.
- Liang Wang,XinGeng,JamesBezdek,ChristopherLekie,KotagiriRamamohanarao “Enhanced Visual Analysis for Cluster Tendency Assessment and Data Partitioning” IEEE Transaction on Knowledge Engineering Vol.22 No.10 October 2010.
- Mahmuddin,Yusof “Automatic Estimation Total Number of Cluster Using A Hybrid Test-and-Generate and K-means Algorithm” ICCAIE 2010 Dec 2010.
- MadhuYedla,Srinivasa Rao Pathakoda “Enhancing K-means Clustering Algorithm with improved Initial Center” IJCSIT pp121-125,2010.
- R.C. Gonzalez and R.E. Woods, Digital Image Processing. Prentice Hall, 2002.
- R.F. Ling, “A Computer Generated Aid for Cluster Analysis,” Comm. ACM, vol. 16, pp. 355-361, 1973.
- T. Tran-Luu, “Mathematical Concepts and Novel Heuristic Methods for Data Clustering and Visualization,” PhD dissertation, Univ. of Maryland, College Park, 1996.
- J.C. Bezdek and R. Hathaway, “VAT: A Tool for Visual Assessment of (Cluster) Tendency,” Proc. Int’l Joint Conf. Neural Networks (IJCNN ’02), pp. 2225-2230, 2002.
- J. Huband, J.C. Bezdek, and R. Hathaway, “bigVAT: VisualAssessment of Cluster Tendency for Large Data Sets,” PatternRecognition, vol. 38, no. 11, pp. 1875-1886, 2005.
- M.Sakthi and Dr. Antony SelvadossThanamani “An Effective Determination of Initial Centroids in K-Means Clustering Using Kernel PCA” International Journal of edComputer Science and Information Technologies, Vol. 2 (3) , 2011, 955-959
- S. Deelers, and S. Auwatanamongkol“Enhancing K-Means Algorithm with Initial Cluster Centers Derived from Data Partitioning along the Data Axis with the Highest Variance” International Journal of Electrical and Computer Engineering 2:4 2007
- K. A. Abdul Nazeer, M. P. Sebastian “Improving the Accuracy and Efficiency of the K-means Clustering Algorithm” Proceedings of the World Congress on Engineering 2009 Vol I WCE 2009, July 1 - 3, 2009, London, U.K.
- RajashreeDash ,Debahuti Mishra , Amiya Kumar Rath , MilluAcharya “A hybridized K-means clustering approach for high dimensional dataset” International Journal of Engineering, Science and Technology” Vol. 2, No. 2, 2010, pp. 59-66.
- Pena J. M., Lozano J. A. and Larranaga P., 1999. An empirical comparison of four initialization methods for the k-meansalgorithm, Pattern Recognition Letters, Vol. 20, No. 10, pp. 1027-1040.
- Valarmathie P., Srinath M. and Dinakaran K., 2009. An increased performance of clustering high dimensional data through
- dimensionality reduction technique, Journal of Theoretical and Applied Information Technology, Vol. 13, pp. 271-273.
- Xu R. and Wunsch D., 2005. Survey of clustering algorithms, IEEE Trans. Neural Networks, Vol. 16, No. 3, pp. 645-678.
- XuJunling, XuBaowen, Zhang Weifeng, Zhang Wei and Hou Jun, 2009. Stable initialization scheme for K-means clustering,
- Wuhan University Journal of National Sciences, Vol. 14, No. 1, pp. 24-28.
|