Keywords
|
| Multilevel inverter, multilevel converter, Cascade inverter, THD, pulse width modulation (PWM) |
INTRODUCTION
|
| The idea of multilevel inverters/converter has been introduced ever since 1975. The term multilevel began with the three-level inverter. Afterward, several multilevel inverters/converter topologies have been developed. However, the concept of multilevel inverters to attain higher power is to use a series of power semiconductor switches with a number of lower voltage dc sources to carry out the power conversion by synthesizing a set of steps voltage waveform [1]. Capacitors, batteries, solar panels, wind turbine and fuel cell can be used as the multiple dc voltage sources. The commutation of the power switches combined these multiple dc sources in order to attain high voltage at the output; however, the rated voltage of the power semiconductor switches depends upon the rating of the dc sources to which they are associated. Multilevel inverters have numerous advantages over conventional 2-level inverters that use high switching frequency pulse width modulation [2]. The attractive characteristics of multilevel inverters can be described as follows. A multilevel inverter is a power electronic system that synthesizes a desired voltage output from a number of levels of dc voltages as inputs. For this reason, multilevel inverters can easily present the high power required of a large electric traction drive. For example, in a parallel-configured HEV, a cascaded H-bridges converter can be used to drive the traction motor from a set of batteries, solar panels, or fuel cells. In a distributed system consisting of fuel cells, batteries, solar cells, etc. the multilevel inverter provides a system to feed these sources into an existing 3- phase power grid. The use of a cascade inverter also allows the converter to control even with the failure of one level of the inverter structure. |
| A multilevel inverter is more proficient than a two-level pulse width modulation (PWM) inverter. This is because the individual devices in a multilevel converter have a much lower dV/dt per switching, and they switch at the much lower frequency rather than at high frequency in PWM-controlled inverters. As a result, the switching losses are very less in a multilevel inverter. Three, four, and five level rectifier inverter drive systems that have used some form of multilevel pulse width modulation (PWM) as means to control the switching of the rectifier and inverter sections have been investigated in the literature. However, a key issue in designing an efficient multilevel inverter is to ensure that the total harmonic distortion (THD) is small enough. To do so require both an (mathematical) algorithm to determine when the switching should be done so that not produces harmonics and a fast real-time computing system to realize the strategy. The present work addresses both of these issues [3]. |
| The many possible pulse width modulation strategies are review with particular regard to their comparative suitability for the modulation of a general multilevel inverter. Carrier based techniques are shown to be the clear choice for both technical and tutorial reasons. Natural and regular sampled PWM are compared with a specific focus on their relative appropriateness for multilevel modulation. The new stress placed on these PWM techniques by the new opportunities opened by multilevel inverters is examined. The mathematical expressions for these pulse width modulation techniques, extended to describe the multilevel waveforms, are examined at the very low pulse numbers which only become relevant for multilevel inverters. The need for a digital implementation of natural sampling is established. Another important modulation method for multilevel inverters is the best possible pulse width modulation (PWM), which includes step modulation, multilevel selective harmonic elimination, and optimal combination modulation. With the identical switching frequency, voltage feature generated by the optimal PWM is improved than that by the popular SPWM or the space vector PWM. The general method for implementing optimal PWM is as follows: based on Fourier series analysis, equation sets whose variables are switching angles are built to meet a precise optimization aim, for example the minimization of total harmonic distortion (THD) of the voltage or the removal of lower order harmonic components of the voltage. An equation set need to be solved with respect to a certain amplitude value of the fundamental voltage component. Usually, the equation sets are nonlinear and transcendental. Several methods, such as the Newton-Raphson iteration method with several variables, methods based on the theory of symmetric polynomials and resultants, and methods based on genetic algorithms, have been proposed to solve nonlinear transcendental equation sets. Calculations based on all the methods above are very lengthy process. Therefore, they cannot be done by a microprocessor or a DSP in real time; they can only do by a computer offline through programming [4]. Switching angles obtained offline have to be stored in a lookup table in a microprocessor or DSP. Therefore, one of the leading drawbacks of the above methods is that they cannot be implemented in real-time due to high operating of the calculations. Another disadvantage is that data of switching angles stored in the lookup table increase if the necessary resolution of the fundamental component of the voltage increases. A multilevel inverter is a power electronic system that synthesizes a preferred voltage output from several levels of dc voltages as inputs. For this reason, multilevel inverters can easily offer the high power requirement of a large electric traction drive. For example, in a parallel-configured HEV, a cascaded H-bridges inverter/converter can be used to drive the traction motor from a set of batteries, solar panels, or fuel cells. In a distributed energy system consisting of fuel cells, solar cells and batteries etc. the multilevel inverter provides a system to feed these sources into an existing 3- phase power grid. The use of a cascade inverter also allows the inverter to operate even with the failure of one level of the converter structure. A multilevel inverter is more efficient than a two-level pulse width modulation inverter [5]. |
MODULATION AND CONTROL TECHNIQUES OF MULTILEVEL INVERTERS
|
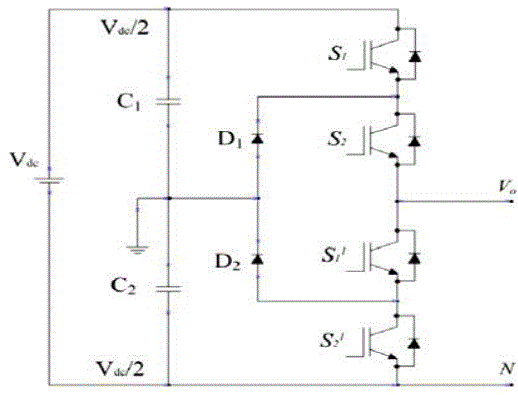
| The recent applications of Multilevel Inverters have a variety including induction machine and motor drives, active rectifiers, filters, interface of renewable energy sources, flexible AC transmission systems (FACTS), and static compensators. The diode clamped inverters, particularly the three-level structure, have a wide popularity in motor drive applications besides other multilevel inverter topologies. However, it would be a limitation of complexity and number of clamping diodes for the DC-MLIs, when the level exceeds three. The FC-MLIs are based on balancing capacitors on phase buses and generate multilevel output voltage waveform clamped by capacitors instead of diode as shown in Fig. 1 [6]. |
| A) Classification of Multilevel inverter control schemes: |
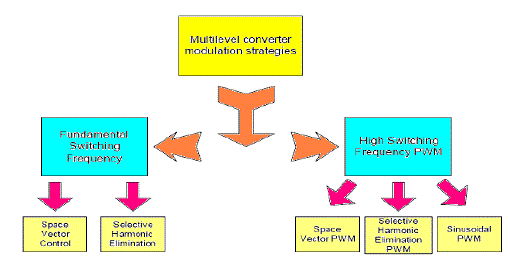
| Several modulation and control techniques have been developed for multilevel inverters including selective harmonic elimination PWM (SHE-PWM), sinusoidal PWM (SPWM), space vector PWM (SVM), and similar variations of the three main algorithms. The modulation methods used in multilevel inverters can be classified according to switching frequencies as seen in Fig. 2 [7]. |
| The SPWM control method is very popular in industrial applications owing to its harmonic reducing opportunities by using several phase shifting options on carrier signal. In the SPWM, a sinusoidal reference voltage waveform is compared with a triangular carrier waveform to generate gate signals for the switches of inverter. Several multicarrier techniques have been developed to reduce the THD ratios, based on the classical SPWM with triangular carriers. Another alternative modulation technique is space vector modulation (SVM) strategy, which has been used appropriately in three-level inverters. The SVM and selective harmonics elimination-PWM (SHE-PWM) methods are fundamental frequency switching methods and perform one or two commutations of the power semiconductors during one cycle of the output voltages to generate a staircase waveform [8]. |
| B) Control schemes of Multilevel inverter (SHE): |
| The efficiency parameters of a multilevel inverter such as switching losses and harmonic reduction are principally depended on the modulation strategies used to control the inverter. As depicted in Fig. 3, multilevel inverter control techniques are based on fundamental and high switching frequency. Three main control techniques of multilevel inverters are SHE-PWM, PWM, and optimized harmonics stepped pulse width modulation (OHS–PWM). The regular PWM modulation method can be classified as open loop and closed loop owing to its control strategy. The open loop PWM techniques are SPMW, space vector PWM, sigma–delta modulation, while closed loop current control methods are defined as hysteresis, linear, and optimized current control techniques [10]. The modulation methods developed to control the multilevel inverters are based on multi-carrier orders with PWM. Due to pre-defined calculations are required, SHE-PWM is not an appropriate solution for closed loop implementation and dynamic operation in multilevel inverters. Among various control schemes, the sinusoidal PWM (SPWM) is the most commonly used control scheme for the control of multilevel inverters. In SPWM, a sinusoidal reference waveform is compared with a triangular carrier waveform to generate switching sequences for power semiconductor in inverter module. Another fascinating control scheme is SVM as one of the most promising control methods in three-phase systems. Despite three-level SVM control is obtained by using two-level SVM, three-level mode is significantly more complex than two-level structure due to increased number of power semiconductors. As a result of this complexity, three-level SVM algorithm is almost implemented using digital signal processors (DSPs) or microcontroller units (MCUs). One of the most important methods to optimize control of the inverter is to select and design appropriate PWM modulation according to inverter topology. The control methods of hybrid multilevel inverters are based on multi-carrier SPWM. Fundamental switching frequency methods shall be selected to reduce switching losses for high voltage modules, while multi-carrier SPWM is selected to control low voltage modules [9]. |
MULTILEVEL CARRIER-BASED PWM
|
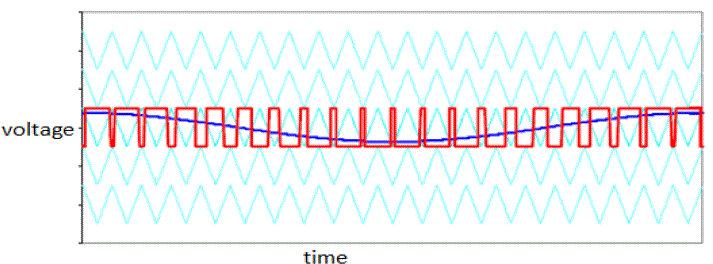
| Several different two-level multilevel carrier-based PWM techniques have been extended as a means for controlling the active devices in a multilevel converter. The most popular and easiest technique to implement uses several triangle carrier signals and one reference, or modulation, signal. Figure illustrates how pulse width of square wave varies with sine wave. It is maximum when amplitude of sine wave is maximum and minimum if amplitude of sine wave is minimum [11]. |
| To extend this technique to multiple phase shifted carriers which are used to form the multilevel waveform requires the carriers to all have equal random sub periods. Here a sub-period is defined as the period of one multilevel switch edge, a sub multiple of the two level PWM period. This ensures complete cancellation of the lowest carrier and sideband spectral terms as before. For complete AC sine wave this technique must applied in both +ve and –ve sides as shown in Fig 4 [12]. |
PULSE WIDTH MODULATION TECHNIQUES
|
| The multilevel PWM waveform, regardless of method of generation, can effectively be considered as the summation of individual two level PWM waveforms. If these two level waveforms are appropriately phased, the amplitude of the voltage steps and hence the amplitude of the harmonic switching frequency terms are reduced in proportion to the number of switch pairs per phase, that is, the number of two level waveforms. The output PWM waveform also switches at an aggregate value which is the sum of the individual two-level switch pair switch frequencies. This places the spectral terms associated with the carrier and sidebands at a multiple of the switch frequency as well. All of the well known modulation techniques for power converters such as selective harmonic elimination, hysteretic and carrier based PWM modulation have been extended to multilevel modulation. In these different modulation techniques, the focus was placed on carrier based PWM techniques and their application to multilevel converters. This is because carrier based PWM [13]. |
| A) Natural and Uniform Sampled Carrier PWM: |
| Multilevel inverters place new demands on these techniques. Since carrier and sideband groups and their multiples associated with the switch frequency can be cancelled and removed from the modulation spectrum, a low switching frequency can be chosen without compromising the output waveform quality. The multiple switch edges due to the many switch pairs still promise a potentially wide modulator bandwidth. To ensure every switching edge influences the output with a minimum delay, triangular carrier (double edge) asymmetric uniformly sampled or naturally sampled PWM are the best choices. Digital or software modulator implementations are by nature uniformly sampled. The accuracy of placement of the switch edges by a digital implementation ensures an exact phase relationship between the switch pair signals. This results in excellent carrier cancellation in the output spectrum [14]. |
| • It is easily implemented using analog or digital circuitry, or software techniques. |
| • It is easily extended to all multilevel converter topologies. |
| • It is shows the good performance at moderate switch frequencies. |
| • It has good dynamic performance, suitable for closed loop control. |
| The understanding of the application of carrier based modulation to multilevel converters leads easily to an understanding of the requirements for and problems of multilevel modulation using other techniques [15]. |
CIRCUIT DESCRIPTION AND ANALYSIS
|
| A) Basic block diagram: |
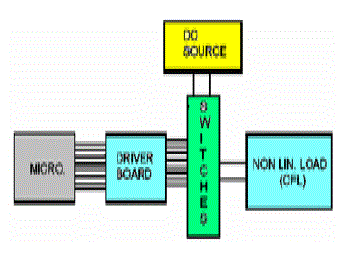
| Block Diagram: Block diagram of multilevel inverter is given in figure. 5 the working of following blocks is follows Microcontroller kit provides the desired signals for switching the MOSFETs at different sequences and different levels Driver board is for driving the MOSFET switches and also for isolation between microprocessor kit and power switches. MOSFET IRF740 is used as a power switch. DC source may be batteries, solar panels or capacitors and nonlinear load is preferred to produce harmonics |
| B) Basic working diagram of driver circuit for one switch: |
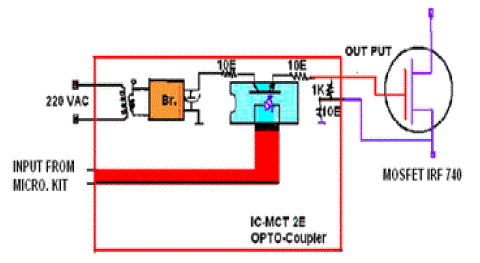
| Driver board is mainly used to isolate Microcontroller (microprocessor Kit) from Switches (Power sw.) and to providing sufficient voltage and current to the MOSFET/SCR/TRIAC. This is a Universal driver card and May be used any power Semiconductor. Input of this board is from micro. Kit and Output goes to switch (MOSFET), as shown in Fig. 6 |
| A) DC Sources and Non Linear Load: |
| DC Source: Dc Sources are here Lead acid batteries. 4-batteries are used in this project (Va, Vb, Vc, Vd) as shown in fig.7.Each of 12 volt. |
| In PWM modulation the width of the pulse is changes according to the amplitude of the sine wave as shown in fig.7 So we generates the square waves of different pulse width (duty cycle) and after filtration sine wave may achieve. |
| B) Cascaded H-Bridges: |
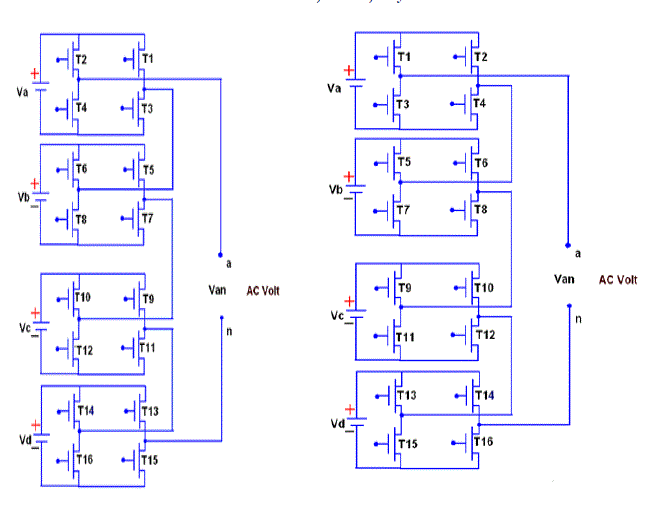
| The series H-bridge inverter appeared in 1975, but several recent patents have been obtained for this topology as well. Since this topology consist of series power conversion cells, the voltage and power level may be easily scaled. An apparent disadvantage of this topology is the large number of isolated voltages required to supply each cell. However, the cells can be supplied by phase-shifted transformers in medium-voltage systems in order to provide high power quality at the utility connection a 1-cell series H-bridge inverter for lower and upper case is shown in Fig. 8 The inverter consist of familiar H-bridge (sometimes referred to as full-bridge) cells in a cascade connection. Since each cell can provide three voltage levels (zero, positive dc voltage, and negative dc voltage), the cells are themselves multilevel inverters. |
| C) Non Linear Load: A non-Linear load that is a CFL (compact florescent Lamp) is used in this project after step-up transformer, to create harmonics Distortions which are then eliminated step by step. In some multilevel converter topologies, the individual PWM waveforms are summed with the aid of passive components, for example inter-phase reactors or flying capacitors. The difference in phase between the PWM waveforms is carried by these components. To reduce the size or ratings of these passive components, it may be better to sacrifice the perfect spectral cancellations of carriers that can be achieved with equal phase shift between triangular carriers, and instead lower the phase difference between PWM waveforms. |
RESULTS
|
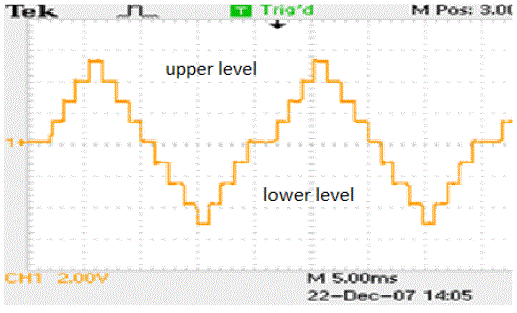
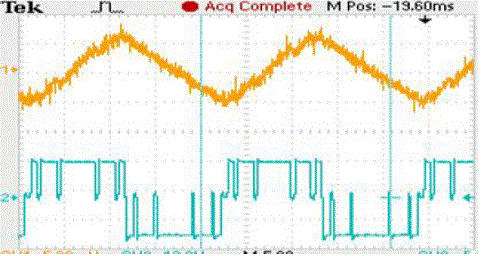
| The wave shapes of nine level inverter is shown in fig. 9 and harmonic are shown in fig. 10 |
| PWM wave is achieved with the help of microcontroller program by switching ON different switches at different time as shown in fig. 11 with blue square wave the width of the wave increases first then decreases with time. Output is also shown with yellow colour wave, this wave is near sine wave, up and steps are shown because no filters are used for removing these irregularities |
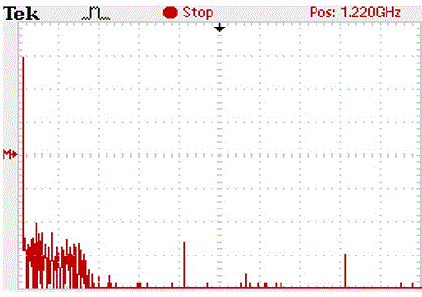
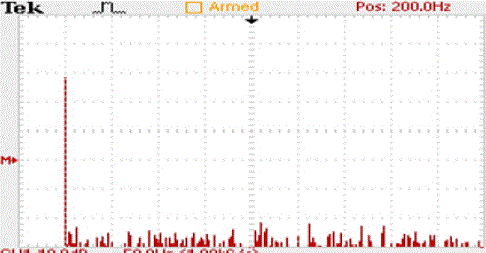
| Harmonics of such a wave is shown in fig.12.as appears with red lines the harmonics disturbances are much and may be reduced up to some extend by using appropriate filters |
| A) Waves after Filteration: |
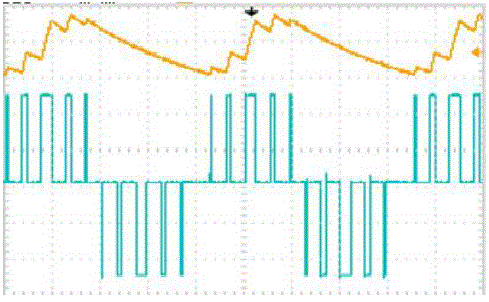
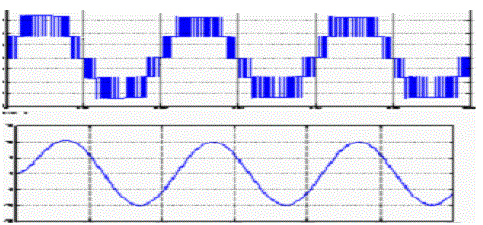
| PWM wave is achieved with the help of microcontroller program by switching ON different switches at different time as shown in fig. 13 with blue square wave the width of the wave increases first then decreases in both positive and negative domain with time, this wave is slightly different as shown in fig.10 because the duty cycle is different. Output after filtration is also shown with yellow colour wave, this wave is sine wave, and filters are used for removing these irregularities (steps). |
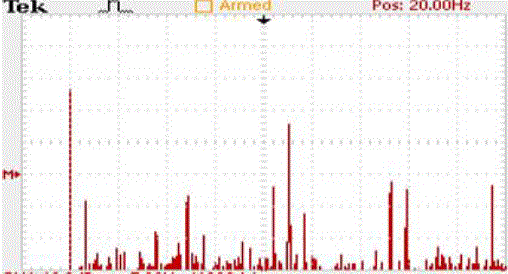
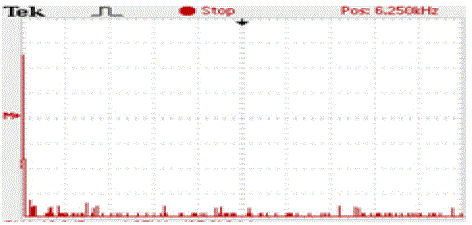
| Harmonics of such a wave is shown in fig. 14 as appears with red lines the harmonics disturbances are less and may be reduced further by using Selective Harmonics Elimination |
| B) Selective Harmonics Elimination: |
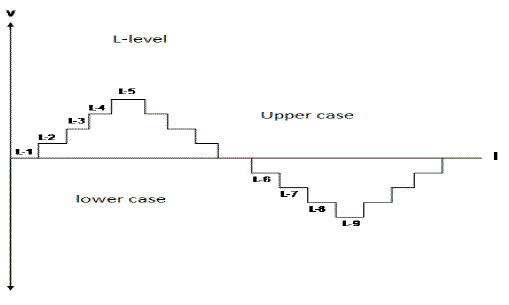
| Selective Harmonics Elimination is basically is combination of fundamental multilevel inverter and PWM switching, as both these. A combination of these two is shown in Fig. 15. The conducting angles, θ1, θ2, θs, can be chosen such that the total Harmonic distortion is a minimum. Normally, these angles are chosen So as to cancel the predominant lower frequency harmonics |
| Harmonics of such a wave is shown in fig.16 as appears with red lines the harmonics disturbances are very less and may be shown the effect of Selective Harmonics Elimination |
CONCLUSION
|
| This paper is concluding the multilevel voltage source inverters. As the ratings of various power electronic switches are limited, multilevel voltage source topologies are useful for high voltage and high power applications along with low harmonics. Among existing multilevel voltage source inverters, three topologies, namely, Diode-Clamped, Flying- Capacitor and Cascaded H Bridge that can be used for multilevel voltage source inverters. It has investigated the performance of various techniques in terms of output voltage spectrum. It is possible to obtain a satisfactory spectral performance with relatively low switching frequency and harmonics. It has been shown that 9- level inverters harmonics spectrum is better, but the programmed selective harmonics elimination method is the best one for many applications that need high dynamic performance in high power application. Moreover, comparative simulation analysis between the different multilevel cascaded inverter control techniques is provided. |
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
|
 |
 |
 |
 |
| Figure 5 |
Figure 6 |
Figure 7 |
Figure 8 |
|
 |
 |
 |
 |
| Figure 9 |
Figure 10 |
Figure 11 |
Figure 12 |
|
 |
 |
 |
 |
| Figure 13 |
Figure 14 |
Figure 15 |
Figure 16 |
|
References
|
- J. Rodriguez, J.-S. Lai, and F. Z. Peng, âÃâ¬Ãâ¢Multilevel inverters: A survey of topologies, controls, and applicationsâÃâ¬Ãâ. IEEE Trans. Ind. Electron.,vol. 49, no. 4, pp. 724-738, Aug. 2002.
- F. Z. Peng, J. W. McKeever, D. J. Adams, âÃâ¬Ãâ¢A Power Line Conditioner Using Cascade Multilevel Inverters for Distribution Systems,âÃâ¬ÃâConference Record - IEEE Industry Applications Society 32nd Annual Meeting, 1997, pp. 1316-1321.
- L. M. Tolbert, F. Z. Peng, âÃâ¬Ãâ¢Multilevel Converters as a Utility Interface for Renewable Energy Systems,âÃâ¬Ãâ in Proceedings of 2000 IEEE PowerEngineering Society Summer Meeting, pp. 1271-1274.
- G. Sinha, T. A. Lipo, âÃâ¬Ãâ¢A New Modulation Strategy for Improved DC Bus Utilization in Hard and Soft Switched Multilevel Inverters,âÃâ¬Ãâ IECON,1997, pp. 670-675.
- S. Sirisukprasert, J.-S. Lai, and T.-H. Liu, âÃâ¬Ãâ¢Optimum harmonic reduction with a wide range of modulation indexes for multilevel convertersâÃâ¬Ãâ,IEEE Trans. Ind. Electron., vol. 49, no. 4, pp. 875-881, Aug. 2002.
- Xu L, Agelidis VG. âÃâ¬Ãâ¢Active capacitor voltage control of flying capacitor multilevel convertersâÃâ¬Ãâ. IEEE Electr Power Appl 2004
- L. M. Tolbert, F. Z. Peng, âÃâ¬Ãâ¢Multilevel Converters as a Utility Interface for Renewable Energy Systems,âÃâ¬Ãâ in Proceedings of 2000 IEEE PowerEngineering Society Summer Meeting, pp. 1271-1274.
- F. Z. Peng, J. W. McKeever, D. J. Adams, âÃâ¬Ãâ¢Cascade Multilevel Inverters for Utility Applications,âÃâ¬Ãâ Proceedings of 23rd InternationalConference on Industrial Electronics, Control, and Instrumentation, 1997, pp. 437-442.
- Belbaz S, Kadjoudj M, Golea N. âÃâ¬Ãâ¢Analysis of the discontinuous PWM strategies applied to the VSIâÃâ¬Ãâ. In: Proceedings of IEEE intsymponcomputational intelligence and intelligent informatics, Agadir (Morocco); 2007.
- J. S. Lai, F. Z. Peng, âÃâ¬Ãâ¢Multilevel Converters - A New Breed of Power Converters,âÃâ¬Ãâ IEEE Transactions on Industry Applications, vol. 32, no. 3,May 1996, pp. 509-517
- Nandhakumar S, Jeevananthan S. âÃâ¬Ãâ¢Inverted sine carrier pulse width modulation for fundamental fortification in DC–AC convertersâÃâ¬Ãâ. In:Proceedings of IEEE power electronics and drive-systems; 2007. p. 1028–34.
- B. Ozpineci, L. M. Tolbert, and J. N. Chiasson, “Harmonic optimization of multilevel converters using genetic algorithms,âÃâ¬ÃâIEEE PowerElectron. Lett., vol. 3, no. 3, pp. 92-95, Sep. 2005.
- S. Sirisukprasert, J.-S. Lai, and T.-H. Liu, âÃâ¬Ãâ¢Optimum harmonic reduction with a wide range of modulation indexes for multilevel converters”,IEEE Trans. Ind. Electron., vol. 49, no. 4, pp. 875-881, Aug. 2002.
- B. M. Song and J. S. Lai, âÃâ¬Ãâ¢A multilevel soft-switching inverter with inductor coupling,” IEEE Trans. Ind. Application., vol. 37, pp. 628-636,Mar./Apr. 2001.S. M. Metev and V. P. Veiko, Laser Assisted Microtechnology, 2nd ed., R. M. Osgood, Jr., Ed. Berlin, Germany: Springer-Verlag, 1998.
- Y. Liu, Z. Du, A. Q. Huang, and S. Bhattacharya, âÃâ¬Ãâ¢An optimal combination modulation strategy for a seven-level cascade multilevel converterbased STATCOM,âÃâ¬Ãâ in Conf. Rec. IEEE IAS Annual. Meeting, Oct. 2006, —. pp. 1732-1737.
|