Keywords
|
| Sparse representation, Opening operation |
INTRODUCTION
|
| Image fusion is an image processing technique that can combine multiple images of the same scene with complementary or redundant information to generate a new composite image with better quality and more features which can provide a better interpretation of the scene than each of the single sensor image can do. In today’s world we deal everywhere with images, specially in remote sensing application. In remote sensing application there are two kinds of images available [1]. Panchromatic [2]. Monochromatic. The panchromatic image acquired by satellites is transmitted with the maximum resolution available and the multispectral data are transmitted with coarser resolution. This will usually be two or four times lower. At the receiver station, the panchromatic image is merged with the multispectral data to convey more information. |
| In remote sensing applications, the increasing availability of space borne sensors gives a motivation for different image fusion algorithms. Several situations in image processing require high spatial and high spectral resolution in a single image. Most of the available equipment is not capable of providing such data convincingly. Image fusion techniques allow the integration of different information sources. The fused image can have complementary spatial and spectral resolution characteristics. However, the standard image fusion techniques can distort the spectral information of the multispectral data while merging. In computer vision, Multi sensor Image fusion is the process of combining relevant information from two or more images into a single image the resulting image will be more informative than any of the input images .Many methods exist to perform image fusion. The very basic one is the high pass filtering technique. Later techniques are based on Discrete Wavelet Transform, uniform rational filter bank, and Laplacian pyramid. |
| Image fusion provides an effective method for comparison and analysis of such data. The ability to combine complementary information from different sources can be used to provide enhanced performance for visualization, detection or classification tasks. In recent years, multisensor image fusion has received significant attention in defense systems, geosciences, medical imaging, robotics and industry engineering, etc. |
| In this paper, inspired by distributed compressed sensing we propose a novel image fusion method based on joint sparse representation (JSR). It can extract and separate the common and innovation features of source images and fuse these features separately. Furthermore, since sparse representation has strong ability to denoise, the proposed algorithm can simultaneously carry out denoising and fusion of the images while corrupted by additive noise. |
FUSION OF NOISY IMAGES WITH JOINT SPARSE REPRESENTATION
|
| The term joint sparsity represents- the sparsity of the entire signal ensemble. The joint sparsity models (JSMs) that apply in different situations can be: JSM-1 (sparse common component innovations), JSM-2 (common sparse supports) and JSM-3 (non-sparse common sparse innovations). JSM-1 is more suitable to solve the problem of image fusion. The method starts with training the over complete dictionary from the entire signal ensemble by K-SVD Then, the common and innovation coefficients are found and denoised simultaneously by JSR, and the fused coefficients are evaluated from these denoised coefficients by using a suitable rule. Finally, the fused coefficients are inverse transformed to obtain the fused image. |
SPARSE REPRESENTATION
|
| Using an over complete dictionary matrix DεRNxM that contains M atoms, {d}M j=1, as its columns, a signal yεRN can be represented as a sparse linear combination of these atoms. The representation of y may either be exact y =Dx, or approximate, y = Dx. The vector xεRM displays the representation coefficients of the signal y. This, sparsest representation, is the solution of either |
| (P0) minx?x?0 subject to y=Dx, |
| (P0,c) minx?x?0 subject to |
| ?y − Dx?2≤ε |
| where ?. ?0 is the l0 norm, counting the non zero entries of a vector. Applications that can benefit from the sparsity and over completeness concepts (together or separately) include compression, regularization in inverse problems, feature extraction, and more. |
SPARSE REPRESENTATION VS JOINSPARSE REPRESENTATION
|
| In the joint sparse representation both the common and innovative features are considered for fusion, while in sparse representation only the innovative features are taken for fusion. |
MORPHOLOGICAL OPENING
|
| In mathematical morphology, opening is the dilation of the erosion of a set A by a where and denote erosion and dilation ,respectively. Together with closing, the opening serves in computer vision and image processing as a basic workhorse of morphological noise removal. Opening removes small objects from the foreground (usually taken as the dark pixels) of an image, placing them in the background, while closing removes small holes in the foreground, changing small islands of background into foreground. These techniques can also be used to find specific shapes in an image |
| (X ⊕ nB) = (X ⊕ B) ⊕ B ⊕…⊕B. |
| Determining distances between spatial objects based on Euclidean metric is a challenge. If all the zones in a cluster considered are identical such that the shapes and sizes of zones are similar, then the simple Euclidean distances between all the possible pairs of centroid of such zones would suffice to detect the spatially significant centroid corresponding to a zone. |
PROPOSED SYSTEM
|
| To overcome the sparse representation a joint sparse representation is used. A novel joint sparse representationbased image fusion method is proposed. Since the sensors observe related phenomena, the source images are expected to possess common and innovation features. We use sparse coefficients as image features. The source image is represented with the common and innovation sparse coefficients by joint sparse representation. The sparse coefficients are consequently weighted by the mean absolute values of the innovation coefficients. Furthermore, since sparse representation has been significantly successful in the development of image de noising algorithms. |
 |
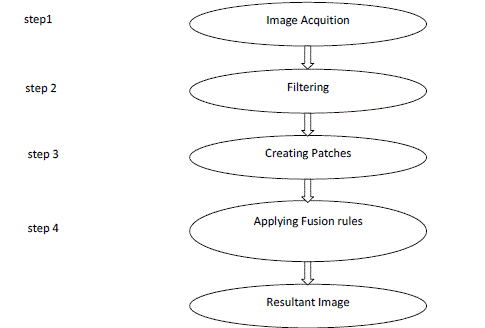
| Methods used consist of the following |
| Image Acquition |
| The remote sensing images are captured and undergone a preprocessing steps to remove the noise in the given image. For noise removing morphological filters are used called opening and closing. These are the best image filters to remove the noise. |
| Filtering |
| Image filters are the purpose of removing noise in the given image. |
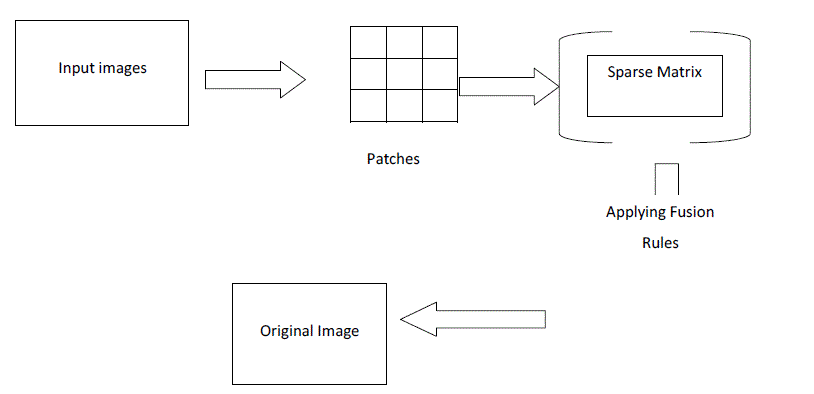
| Creating Patches |
| Patches are dictionary like format which consist of small atoms collection which is the parts of the given images. Then using the patches sparse matrix has been created, in which that sparse matrix rules are going to apply. |
 |
CONCLUSION
|
| A original model for image fusion using joint sparse representation is choosed. This would make use of the sparse representation points of all the source images by pick up the common and innovative features of the source image from the dictionary which has been trained and fused simultaneously. The image is reconstructed from the fused image. |
References
|
- Xiao Xiang Zhu, Richard Bamler ‘A Sparse Image Fusion Algorithm With Application to Pan-Sharpening’, IEEE Transactions, vol. 51, no. 5, May2013.
- Cheng, H. Zhang, H. Shen, and L. Zhang, ‘A practical Compressed sensing-based PAN- Sharpening method,’ IEEE Transaction vol. 9, no. 4, pp.629–633, Jul.2012.
- Li .S and Yang B, ‘A new pan-sharpening method using a compressed Sensing technique,’ IEEE Transactions, vol. 49, no. 2, Feb. 2011.
- Milindkumar V. Sarode, Prashant R. Deshmukh, ‘Evaluation of Fusion and Denoising Algorithm for Multi focus Images’, Proceedings, VolII,July 2011.
- Naidu V.P.S., ‘Image Fusion Technique using Multi-resolution Singular Value Decomposition’, Defence Science Journal, pp. 479-484, vol. 61, no.5,September 2011.
- PrakashNK ,‘ International Journal of Enterprise Computing and Business Systems’, ISSN, vol. 1 issue 2 July 2011.
- Shah.V. P and N. H. Younan, ‘An efficient pan-sharpening method via a combined adaptive PCA approach and contourlets,’ IEEE Transactions, vol.46, no. 5, pp,May 2008.
- Tu, S. Su, H. Shyu, and P. Huang, ‘A new look at IHS-like image fusion methods,’ IEEE Transactions , vol. 2, no. 3, pp. 177–186, Sep. 2001.
- Wang, X. ‘Compressive sensing for pan-sharpening,’ M.S. thesis, Tech. Univ. Munich, Germany, 2011.
- Zhu X and. Bamler R, ‘Tomographic SAR inversion by L1 norm Regularization The compressive sensing approach, ’ IEEE Transactions, vol. 48, no.10, pp. 3839–3846, Oct. 2010.
-
|