Multi Sensor Image Fusion using Empirical
Mode Decomposition

Sakthipriya V.S; VPS Naidu

Multi Sensor Image Fusion using Empirical Mode Decomposition

Sakthipriya V.S¹ and VPS Naidu²

Dept. Of Instrumentation Engineering, Madras Institute of Technology, Chennai, India
MSDF Lab, CSIR-National Aerospace Laboratories, Bangalore, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Image fusion is a process of combining relevant information from two or more images from different sensors based on certain algorithm. Many algorithms have been proposed for pixel level image fusion. In this paper, Empirical Mode Decomposition is the recent, powerful tool for adaptive multi scale analysis of non stationary signals that decomposes them into Intrinsic Mode Functions (IMFs). Hence an attempt is made to use EMD for multi sensor image fusion. Two types of Empirical Mode Decomposition algorithms viz. BEMD (Bi dimensional Empirical Mode Decomposition) and VEMD (Vectorized Empirical Mode Decomposition) are used to decompose the images to get Intrinsic Mode Functions (IMFs). It is concluded that both algorithms are performed similar but VEMD is computationally very simple. Fusion algorithms viz., Simple Averaging (SA), Principal Component Analysis (PCA), Stationary Wavelet Transform (SWT) and Laplacian Pyramid (LP) are applied on each IMFs to generate the fused IMFs. Fused image is reconstructed by summing all the fused IMFs. Objective and subjective fusion quality evaluation metrics are used to evaluate the performance of these fusion algorithms. It is concluded that SWT based image fusion algorithm performs better followed by LP based fusion algorithm. It is also concluded that fusion quality is degraded by using more number of decomposition levels in wavelets and pyramid based image fusion algorithms. From this study, it is concluded that both BEMD and VEMD with SWT based image fusion algorithm provides good fusion results. VEMD with SWT based image fusion algorithm is computationally simple and can be used for real time image fusion applications.

Keywords

Image Fusion, Empirical mode decomposition, Performance Metrics.

INTRODUCTION

Empirical Mode Decomposition (EMD) was first introduced by Huang et al. [1] and provides a powerful tool for adaptive multi scale analysis of non stationary signals. It is a non-parametric data-driven analysis tool that decomposes non-linear non-stationary signals into Intrinsic Mode Functions (IMFs). The final representation of signal is an energyfrequency distribution, designated as Huang spectrum [1] that gives sharp identifications of salient information. With the Hilbert transform, the IMFs allow representation of instantaneous frequencies as functions of time. The main conceptual benefits are the decomposition of parent signal into IMFs and the visualization of time-frequency characteristics.

A. BEMD

EMD has many interesting features and an important feature is, it is fully adaptive multi scale decomposition. This is because EMD operates on the local extremum sequence and the decomposition is carried out by direct extraction of the local energy associated with the intrinsic time-scales of the signal itself. This is different from the wavelet-based multi scale analysis that characterizes the scale of a signal event using pre-specified basis functions. Owing to this feature, EMD is highly promising in dealing with other problems of a multi scale nature. EMD found various advantages and it can be useful for two dimensional data analysis [1] [2].

An image is a bi dimensional IMF if it has a zero mean, if the maxima are positive and the minima are negative and if the number of maxima equals the number of minima. Bi dimensional empirical mode decomposition (BEMD) method is a relatively new, but potential image processing algorithm. BEMD decomposes an image into multiple hierarchical components known as bi dimensional intrinsic mode functions (BIMFs) and a bi dimensional residue, based on the local spatial variations or scales of the image.

In BEMD using Finite Element method, the local mean surface of a two-dimensional dataset is generated directly from the characteristic data points rather than from the upper and lower envelopes. This overcomes the problem of possible over shootings between the upper and lower envelopes. Our method avoids constructing two different two dimensional interpolating surfaces (the upper and lower envelopes), which is normally a difficult task and requires much computational cost. In addition, the characteristic data points in our method include not only the local maxima and minima, but also the saddle points, which are a distinct feature of two-dimensional data. In this paper, finite element method is used for fusing the images using EMD [3].

B. VEMD

Bi dimensional Empirical Mode decomposition (BEMD) is computationally complex and involves a series of steps. As it is two dimensional, every row and column have to be processed separately. This in turn will increase the computation of algorithm and on the other hand it is time consuming. BEMD by finite element method is not mathematically strong which further adds its disadvantage. Interpolation error will also be present and triangle mesh formation using Delaunay method will also introduce its own error, which in turn paved a way for a faster, computationally inexpensive algorithm called Vectorized Empirical Mode decomposition (VEMD) [4]. The algorithm of VEMD is simple and is explained as below. Converting a two dimensional data to one dimension and then employing the one-dimensional EMD could be an efficient approach to deal with some image processing problems. This process would be fastest as expected than the other EMD methods. An image is vectorized and one dimensional EMD is applied to two vectors and this process is called VEMD. The image I(x,y) of size MxN is divided into rows and concatenates these rows to form a 1D vector data I( x ) whose size would be MN . 1D EMD is the applied on the resultant vectorized data. The resultant fused signal is converted back into the image by reversing the procedure.

IMAGE FUSION

Various image fusion algorithms are in literature and an attempt has been made to fuse the images using empirical mode decomposition. The images to be fused are decomposed to several IMFs using the above BEMD process. Fusion is performed at the decomposition level and the fused IMFs are reconstructed to realize the fused image. The decomposed IMFs of the images are fused using four methods viz. Simple Averaging, Principle Component Analysis, Discrete Wavelet Transform and Laplacian pyramid [5][6][7]. An important point to note in image fusion using EMD is that the number of IMFs should be fixed. The number of IMFs can be different for two images and fusion of IMFs is not possible. Hence the number of IMFs should be fixed in the fusion process. One of the important prerequisites to apply fusion techniques to source images is the image registration, i.e., the information in the source images is needed to be adequately aligned and registered prior to fusion of the images. In this thesis, it is assumed that the source images are already registered.

RESULTS AND DISCUSSION

Reference image along with images to be fused are used to compare the fusion performance of BEMD and VEMD based fusion algorithms. First image set contains out of focus images and the second image set contains multi spectral images. First section explains about the image fusion of multi focus images followed by the image fusion of multi spectral images.

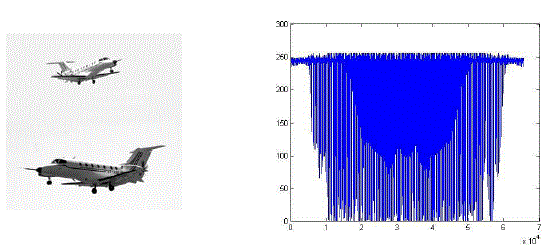
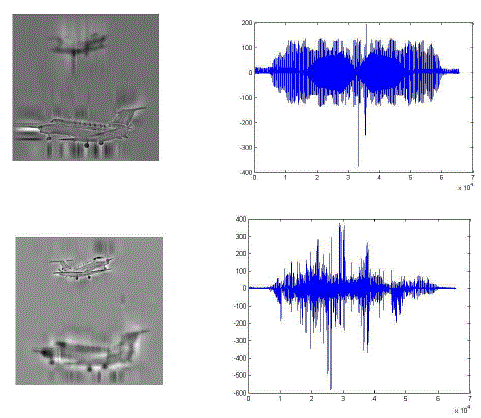
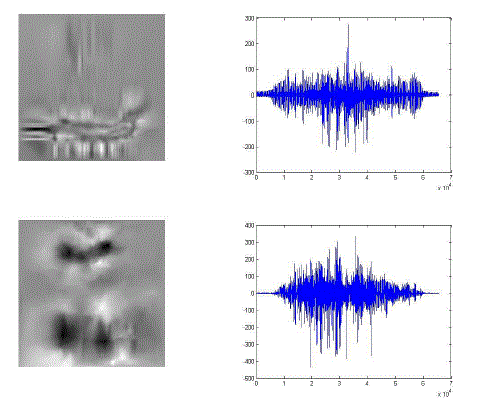
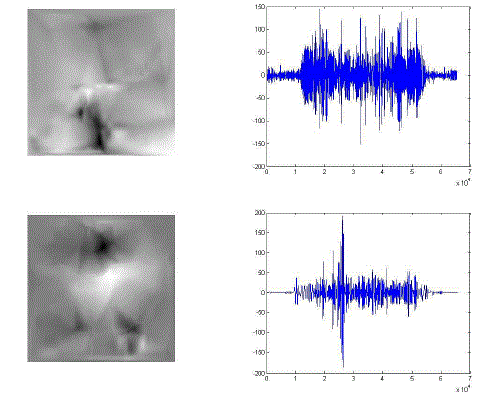
The results for fusion of multi focus images using VEMD and BEMD are discussed here. The National Aerospace Laboratories indigenous aircraft SARAS, shown in Fig. 1a is considered as a reference image (left half: true image and right half: represented in vector form) to evaluate the performance of the fusion algorithms. The complementary pair input images and are taken to evaluate the fusion algorithm and these images are shown in Fig. 1b. The complementary pair has been created by blurring the reference image with a Gaussian mask at the top and bottom half respectively. The IMFs of each image after applying VEMD and BEMD are shown in the Figure 2a – 2d (1st column: with BEMD & 1nd column: VEMD).

The IMFs of each images obtained using VEMD and BEMD are fused using four methods viz. Simple averaging (SA), Principle Component Analysis (PCA), Stationary Wavelet Transform (SWT) and Laplacian Pyramid (LP). The fused image and error image using BEMD with SWT is shown in Fig-3a and similarly, fused image and error image using VEMD with SWT is shown in Fig-3b. All the fused images look similar from visual point of view.

The fused image and error image using BEMD with LP is shown in Fig-4a and similarly, fused image and error image using VEMD with LP is shown in Fig-4b. From Fig-3 and Fig-4, it is observed that SWT based image provides better fusion results.

Most commonly used performance metric for objective evaluation are Root Mean Square Error (RMSE), Peak Signal to Noise Ratio (PSNR), standard deviation (SD), spectral angle mapper (SAM), correlation coefficient (CC), maximum difference (MD), visual information fidelity of fusion (VIFF) and execution time etc.. Various other performance metrics are available for the objective evaluation of image fusion quality [5][8][9][10]. Fusion quality evaluation metrics for both BEMD and VEMD algorithms are shown in Table 1. It is observed that RMSE is smaller when compared with the pixel level image fusion presented in Ref. [5]. It shows that the present algorithm had performed well. Table 2 shows the RMSE values for increasing number of IMFs with the increase number of wavelet decomposition levels in fusion process. It is observed from the table that three levels of wavelet decompositions gave less RMSE values for both BEMD and VEMD algorithm. The error value is less if IMF=2 and the value increases for the increasing number of IMFs for BEMD algorithm. In case of VEMD, the error value is less for IMF=1 and the error increases with the increasing IMF number. VEMD decomposes image up to 11 IMFs and BEMD decomposes the image up to 24 IMFs. Hence for VEMD, we cannot increase the IMFs beyond 11. Table 3 shows the RMSE values for increasing the number of IMFs with the increasing the number of LP decomposition levels in fusion process. It is observed from the table that 2 levels of pyramid decompositions gave less RMSE values for both BEMD and VEMD algorithm. The error value is less if IMF=2 and the value increases for the increasing number of IMFs for BEMD and VEMD algorithm. In this case also, BEMD performs better than VEMD with the expense of computational complexity.

CONCLUSION

Two types of Empirical Mode Decomposition algorithms viz. BEMD (Bi dimensional Empirical Mode Decomposition) and VEMD (Vectorized Empirical Mode Decomposition) are used to decompose the images to get Intrinsic Mode Functions (IMFs). Performances of these algorithms are evaluated. By performance evaluation metrics, it is concluded that both algorithms are performed similar but VEMD is computationally very simple. Hence VEMD can be adopted for real time applications. Fusion algorithms viz., simple averaging (SA), principal component analysis (PCA), Stationary wavelet transform (SWT) and Laplacian pyramid (LP) are applied on each IMFs to generate the fused IMFs. Fused image is generated by summing all the fused IMFs. Fusion quality evaluation metrics are used to evaluate the fusion algorithms. It is concluded that SWT based image fusion algorithm performs better followed by LP based fusion algorithm. It is also concluded that fusion quality is degraded by using more number of decomposition levels in wavelets and pyramid based image fusion algorithms.

ACKNOWLEDGMENT

We would like to thank Mr. N Santhakumar, MSDF group Head, FMCD Department, CSIR-NAL and Prof. J. Prakash, Head, Dep. of Instrumentation Engg., Madras Institute of technology, Madras, for their constant encouragement and support to carry out this work.

Tables at a glance


Table 1	Table 2	Table 3	Table 4	Table 5

Figures at a glance


Figure 1	Figure 2a	Figure 2b	Figure 2c


Figure 2d	Figure 3	Figure 4

References

N. Huang, Z. Shen, S. Long, M. Wu, H. Shih, Q. Zheng, N. Yen, C. Tung, and H. Liu, “The empirical mode decomposition and Hilbertspectrum for non-linear and non-stationary time series analysis,” Proceedings of the Royal Society A, vol. 454, pp. 903–995, 1998.

G. Rilling, P. Flandrin and P. Goncalves, “On empirical Mode Decomposition and Its Algorithm”, IEEE-EURASIP Worshop on NonLinear Signal and Image Processing NSIP-03.

Ciarlet, P. G, “Numerical analysis of the finite element method”, Seminaire de Mathematiques Superieures, No. 59, 1976.

Vaidehi.V et. al, “Fusion of Multi-Scale Visible and Thermal Images using EMD for Improved Face Recognition”, IMECS , Vol I, 2011.

VPS. Naidu and J.R. Roal, “Pixel-level Image Fusion using Wavelets and Principal Component Analysis”, Defence Science Journal, Vol.58, No. 3, pp. 338-352, May 2008.

H. Li, B.S. Manjunath, and S.K. Mitra, “Multi-sensor image fusion using the wavelet transform”, Proceedings of the conference on‘Graphical Models and Image Processing’, pp. 235–245, 1995.

Burt, P.J. Kolczynski, R.J., “Enhanced image capture through fusion”, Fourth International Conference on Computer Vision, Berlin,Germany, 173-182, 1993.

Wang, Z. & Bovik, A.C. “A universal image quality index”, IEEE Signal Processing Letters, Vol. 9(9), 81-84, March 2002.

Yu Han, Yunze Cai, Yin Cao, Xiaoming Xu, “A new image fusion performance metric based on visual information fidelity”, Informationfusion, Vol. 14, Issue 2, pp.no 127-135, April 2013.

Xuande Zhang, Xiangchu Feng, Weiwei Wang, and Wufeng Xue, “Edge Strength Similarity for Image Quality Assessment”, IEEESignal Processing letters, Vol. 20, No.4, 2013.