Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Multiband Fractal Antenna for wireless communication

Ancy P V1, Satya Bhushan Sukla2,A K Prakash3, K K Mukundan4
  1. M Tech Electronics, TocH Institute of Science and Technology, Kerala , India
  2. Sci /Engr ‘SD', ADRFD/RFSG/AVN, VSSC, Thiruvananthapuram, India
  3. Professor, TocH Institute of science and technology, Kerala, India
  4. Sci /Engr ‘SG', ADRFD/RFSG/AVN, VSSC, Thiruvananthapuram, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Wider bandwidth is required in modern wireless communication. Traditionally each antenna operates at a single frequency band, where a different antenna is needed for different application. This will take more space for occupation. This paper presents a novel multiband fractal antenna for wireless communication. Fractals have self similar shapes and space filling properties. This property makes the fractal antenna compact and operating in multiband frequencies. The fractal antenna is formed by applying a generator shape repetitively at a constant scale factor and results in an antenna with log-periodic characteristics which is a multiband antenna and a miniaturization characteristic. ISM band (Industrial, Scientific and Medical bands) and GSM band are mostly used wireless bands. The operating frequencies of proposed fractal structure cover two GSM bands and one ISM band. Sierpinski and Minkowski fractal structures are simulated. Fractal with PIFA structure compromise size reduction. PIFA is one of the most promising antenna types because it is small and has a low profile, making it suitable for mounting on portable equipment. Sierpinski-PIFA gives 35% size reduction and 60% size reduction is possible using Minkowski- PIFA structure. The radiating element is etched on Nalco substrate with dielectric constant of 4.2. The Antenna was simulated using CST Microwave Studio based on FDTD method. Antenna design is discussed in detail and results obtained are presented here.



 

Keywords
GSM band, ISM band, Fractal, PIFA structure and CST Microwave studio

INTRODUCTION
Constrains on wireless antenna design include requirement for multi-band resonance. Dual band, tri band, quad band, and dual mode cellular phone is an example of a multiple frequency wireless devices. Dual band operation involves transmitting and receiving in both 850 MHz and 1900 MHz frequencies in GSM mode where as dual mode involves operating in both CDMA and GSM modes. Traditional antennas are unable to meet these requirements and hence alternative approaches are needed. Reconfigurable antennae using it multiband antennae can be obtained. Generally reconfigurability can be obtained using following techniques: Tunable elements in feeding networks, adaptive matching networks, phase shifters and tunable filters, tunable elements embedded such as PIN diode, MEMS and optimal switching in the radiating elements. But it is bulky and we get one band at a time. So recent antenna developments have applied fractal mathematics to antenna design, resulting in new fractal antennas with multi-band behavior.

FRACTAL CONCEPT
Fractal antennas are reliable and cost-effective. Fractal antennas allow for multiband capabilities, decreased size, and optimum smart antenna technology. Fractals have self similar shapes and space filling properties that can be subdivided into parts. This property makes the fractal antenna compact and operating in wideband frequencies. The different fractal elements of the antenna allow it to have different resonances. The presence of discontinuities in the geometry increases the bandwidth and radiation properties of antenna. It also has long electrical lengths that fit into a compact size[5]. There are many mathematical structures that are fractals; e.g. Sierpinski’s gasket, Minkowski ,Cantor’s comb, von Koch’s snowflake, the Mandelbrot set, the Lorenz. attractor, etc
Fractal characteristics
1) Multiple electrical dimension, multiband or wideband, and ratio between adjacent resonant frequencies is proportional to the fractal dimension.
2) Miniaturized and compact, filling space effectively. (It also has long electrical lengths that fit into a compact size)
3) Self-loaded to 50, auxiliary reactance and capacitance not needed.
4) Mutual coupling between array elements can be reduced substantially.
5) For multiband only single feed is required.
6) The presence of discontinuities in the geometry increases the bandwidth and radiation properties of antenna

COMPARISON BETWEEN DIFFERENT FRACTAL STRUCTURES
Sierpinski is designed by dividing normal square patch into nine equal parts and removing centre portion. Normal patch is responsible for lower frequency and slot is responsible for higher frequency. Width and length of simulated sierpinski antenna is 39 and 30 respectively.
The Minkowski fractal antenna is designed based on a square generator structure.
W1(n+1) = a1xLn
W2(n+1) = a2xLn
W1 is the middle segment width and W2 the indentation width. a1 is the W1/L0 ratio and a2 is the W2/L0 ratio. n is the iteration number. The initial value of the square length L0=30 mm is found from a typical microstrip patch calculation formula. [7]
Figure 4 shows the simulated Sierpinski and minkowski fractal structures. Substrate used for antenna is FR-4 with dielectric constant of 4.2.
Frequency, Return loss, Bandwidth and Size of both structures are compared in table 1.
Table 1 shows that Simulated sierpinski structure tuned to 2.08GHz and 6.7GHz frequencies .Minkowski structure gave 410MHz and 2.24GHz. For the same dimension (~30mm) minkowski could tuned to 410MHz,but sierpinski tuned only to 2.08GHz. That means for low frequency minkowski is more suited since its dimension is less compared to sierpinski for same frequency.So minkowski fractal structure is selected for proposed antenna.

SIZE REDUCTION USING FRACTAL STRUCTURE
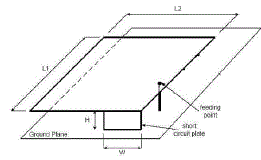
From different fractal analysis minkowski structure is most suited one when we consider size reduction. By introducing PIFA(Planar Inverted F Antenna) with fractal structure miniaturization is again possible .PIFA can reduce the possible electromagnetic energy absorption by the mobile handset since it have relatively smaller backward radiation toward the user. However, PIFA have some drawbacks such as low efficiency, narrow bandwidth and not multiband. To enhance these drawbacks, especially narrow bandwidth, and to meet the miniaturization requirements of mobile units, Fractal PIFA has been designed[9]. Figure 5 shows PIFA structure.
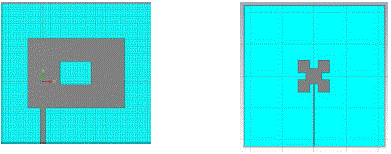
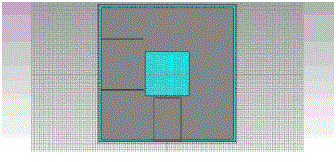
Sierpinski with PIFA structure is simulated using CST Microwave Studio. Simulated structure is given in Figure 6.
Size of a patch antenna is always comparable to quarter wavelength. Maximum size of a patch antenna corresponds to the lowest frequency of multiband antenna. In this case, first GSM Band(800MHz), is the lowest frequency For first GSM Band(800MHz) , dimension is 94mm.That is without PIFA structure, sierpinski fractal have dimension of (~100x100)mm .Using PIFA structure along with sierpinski fractal , the size of the antenna is reduced to (65x65)mm. That means 35% size reduction is possible using PIFA structure.
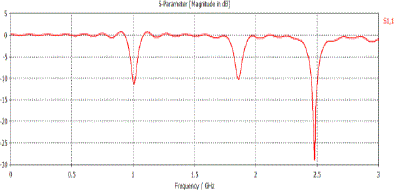
Return loss of Sierpinski PIFA structure is given in figure 7.
From the return loss curve it is clear that required three bands are obtained. The three frequency bands with corresponding bandwidth are given in table 2.
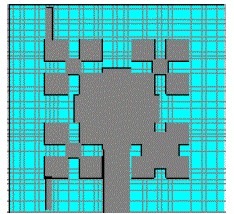
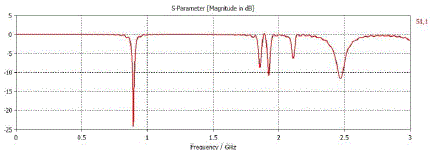
For Minkowski-PIFA structure ,initial length L0 is 40mm . That is the size of the structure is 40mm and two iterations are done. From this 60% size reduction is possible. Return loss is given in Figure 9.
Table 3 shows frequency bands and corresponding bandwidths.
All these bands are useful in various wireless applications specifically, Band 1, Band 2,Band 3 for GSM ,Band 4 for 3G services and Band 5 for ISM band.

CONCLUSION
In this paper analysis different classical fractal structures separately and select minkowski structure which met required frequency bands. Combing fractal structure with PIFA miniaturization is possible. From simulation result it is shown that minkowski second iteration gave more reduced antenna. By combining minkowski with PIFA structure antenna size is again reduced (60% reduction)and which meet required size for wireless communication.

Tables at a glance
Table icon Table icon Table icon
Table 1 Table 2 Table 3

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 3
Figure 5 Figure 6 Figure 7 Figure 9

References