Keywords
|
| Multi-Sensor Image, Improved Harris Corner Detector (HCD), Discrete Particle Swarm Optimization, and Multi-Objective Optimization. |
INTRODUCTION
|
| Image Registration [1] is a process of aligning the image obtained from either different sensor, at different times, different View point with the reference image. The image on which the registration process is done is called as base or reference image and the image which is registered is known as the sensed image. |
| Basically, process of Image Registration involves two types such as area based registration [1] and feature based registration [2]. Area based method is based on detecting the overlapping region in the reference(base) image and sensed image using correlation mutual information and standard deviation and other probabilistic or statistical tool applied on an area or a region of interest. Feature based Technique search for common features (edges, junctions, points, boundaries, etc of an object) between the reference image and the sensed image (floating) and provide a mathematical transformation which map the sensed image to the reference image. |
| Hence there doesn't exist any robust method for registering multi-temporal and multi-sensor image in the literature. Earlier Feature mapping was done manually which was intensive and was subjected to human error and bias. Additionally, some semi-automatic method based on a angle had been used for matching points. To overcome these Random Sample Consensus (RANSAC) was used as a matching technique, RANSAC was used to match point automatically by classifying the points detected into inliers and outliers. However in several instances it was observed that the RANSAC picks point from the outliers. Followed by RANSAC, the various variants of RANSAC have been proposed named Maximum Likelihood Estimation Sample Consensus for estimating the image geometry by sampling points. The same techniques has extend to Maximum A Posteriori Sample Consensus [7] which takes posteriori Probability into Account. Therefore a more efficient method was then proposed by incorporating population based method such as Genetic Algorithm (GA) [9] and Particle Swarm Optimization (PSO) along with RANSAC to find the best match. |
| In earlier study, RANSAC [5] and Particle Swarm Optimization have been successfully applied for matching correspondence between same sensor images. In this paper, distance condition was sole fitness function for matching correspondences, but this fail in case images are of different resolutions, in this new approach is proposed based on improved Harris Corner Detector (HCD) for detecting the feature points and optimizes the match using DPSO based on multi-objective functions (distance and angle). The fitness functions are evaluated using objective switching method. The performance of image registration is evaluated using quality measures. |
PROBLEM FORMULATION
|
| For registration of multi-sensor images, only distance condition [12] as the fitness functions is not sufficient as the images are of different scales. For accurate registration of such images, better matching is obtained by include angle [13] as fitness criterion beside distance. The combination of two fitness function will give better matching of the corner points in the reference and the sensed image. |
| Let U and V represents the set of corner points detected in base (reference) image and input image. |
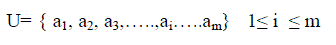 |
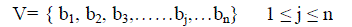 |
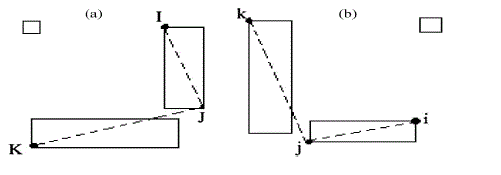
| Where the co-ordinated of points ai and bj is given by (xai, yai)and (xbj,ybj) in their respective co-ordinated system. Multisensor satellite images can be registered using the affine transformation which takes into account scaling, rotating and translation. A set of three matched points is necessary to obtain the registered image. Hence the points considered for features matching in base image (I, J, K} and input image {i, j, k} . |
| A. Distance condition |
| In general, a distance between two points p and q is given in Eqn.2 |
| D = || p-q || (3) |
| Similarly considering these distance condition for our reference and sensed image namely (I, J, K} and {i, j, k}. respectively. The distance between the corner points I, J and K in fig. 1(a) is given by the forms of difference between the two points as show in |
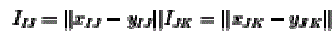 (4) (4) |
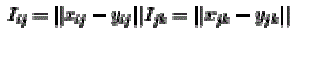 (5) (5) |
| Similarly the distance evaluated between the distance of the corresponding corner points in the reference and sensed image are obtained using |
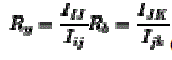 (6) (6) |
| The absolute difference of ratio R y and R b is within the threshold’s’ set. The distance condition aim to minimize the difference of the norm of the ratio of the corresponding distance in the reference and sensed image. For a good match R y must be equal to Rb. |
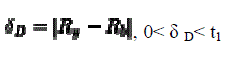 (7) (7) |
| The deviation in the distance ratio δDas represented in (6) lies within the threshold t1 , then the distance condition is satisfied. The constraints involved in this case are as follows only three points are considered while evaluation the fitness function and here threshold t1 is user defined. |
| B. Angle condition |
| Angle condition represents the minimization of the difference in the corresponding angles measured in the reference point and sensed point chosen from the reference and sensed image respectively from fig. 1(a) , let the slope between points I, J and K is given by |
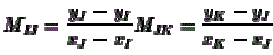 (8) (8) |
| Similarly from Fig .1(b) the slope of the line segment between points I , j and k are shown in |
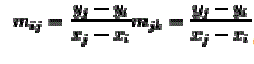 (9) (9) |
| From the co-ordinated geometry , the angle enclosed between slope m IJ and m JK in the reference image is given by |
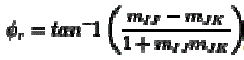 (10) (10) |
| Similarly, the angle between slope m ijand m jk in the sensed image is given by |
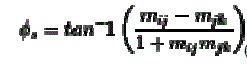 (11) (11) |
| If the points are correctly picked then |
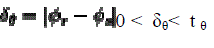 (12) (12) |
| The difference between the angles should be less than the threshold t θ .The constraints involved in the angle conditions are first, the differences in the corresponding angles should be less than the threshold t θ which is referred in Eqn. (11) then the angle of three corresponding points, should be considered here. |
| Let us consider f1(x) corresponds to the distance condition and f2(x) corresponds to the angle condition. |
| Mathematically, this optimization procedure can be formulated as |
| Minimize distance : Min { d=f1 (x) } |
| Subject to the constraints involved in (6). |
| Minimize angle : min { a=f2 (x) } |
| Subject to the constraints involved in (11). |
| The objective function f1 (x) may be conflicting with other objective function (i.e) f2(x) , thus most of time it is impossible to obtain for all objective the global minimum at same point. |
| C. Multi-objective optimization |
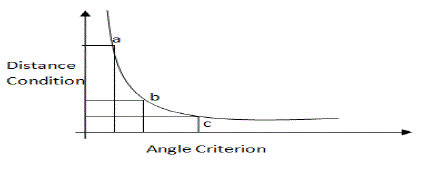
| In many situations, objective functions are taken into account which conflict with each other. For instance optimizing x with respect to one objective function may not optimize some other objective function. In reality as it is impossible to minimize each objective function, hence it is easier to find x such that it satisfies the entire objective function at an acceptable limit without any domination of any objective function over the other. |
| The above graph explains the nature of conflicts in any optimization process. In this study, distance represents one objective function and angle represents another objective function. Both of them are subject to minimization. In Fig. 2 point ‘a’ is a point where distance condition is violated while angle condition is satisfied. ‘C’ is where angle condition is violated where distance condition is satisfied and point ‘b’ represents a location where both the objective functions are minimum. This leads to find the best pare to optimal solution. A set of optimal trade off which forms the solution is said to be Pareto Set. |
METHODOLOGY
|
| This Section describes the methodology involves in feature based image registration using DPSO (Discrete Particle Swarm Optimization). |
| A. Point detection by harris corner detector |
| Due to invariance to noise, illumination and affine parameters, Harris Corner Detector (HCD) [14] is considered superior to precedent method proposed by Moravec. Here an improved Version of Harris Corner Detector (HCD) is used in extracting the corner points in the reference and sensed images. |
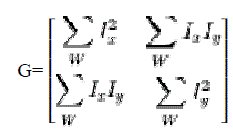 (13) (13) |
| Where Ix andIyare gradients of the intensities along X and Y direction. |
| Now we considering (1), (2) which involves U and V, U represents the set of m points detected for the reference image and V represents the set of n points for the sensed image. |
| B. DPSO (Discrete Particle Swarm Optimization) |
| The corner points of the sensed image are matched with the corner points of the reference image using DPSO. Instead of using brute force method of finding the corresponding corner points in the sensed and the reference images. DPSO Optimizes the search for the set of global best matched points based on the distance and angle condition utilizing the objective switching technique. Here it treats every points in a vector as discrete entities. A typical vector is shown in |
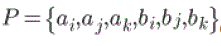 (14) (14) |
| RANSAC uses a single point for point correspondence while DPSO treats the cluster base points and its corresponding input as discrete entities of non-repeating whole number stored in position Vector (X i) as said earlier. This is an associated fitness value to indicate its correspondence. |
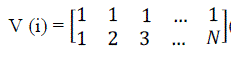 (15) (15) |
| In (14) first row represents proportional likelihood associated with the corresponding attribute or it is a weight associated with a particle attributes in the same column, second row indicated the attributes which contain indices of the cornet points, initially all the weights are defined as one, then the total number of point is N. |
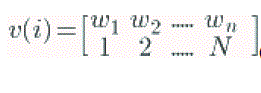 (16) (16) |
| wj = 1+ α * δ (α) + β * δ (β) + γ * δ (γ) |
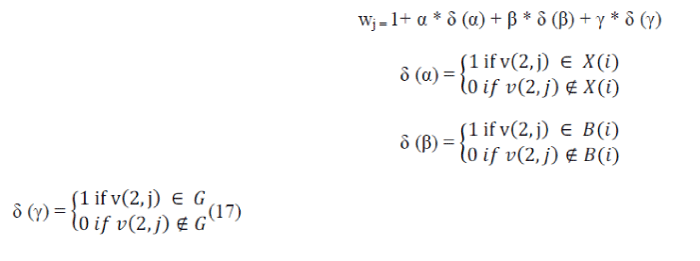 |
PERFORMANCE MEASURE
|
| A. Feature correspondence measure |
| The feature matching accuracy is measured by checking how many times the DPSO matches the features correctly in the reference and sensed image out of the total number of matched point satisfying the multi-objective function to test the novelty of the algorithm, it is run for several times. The accuracy of the matching is shown in |
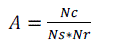 (18) (18) |
| Where Ncis the total number of correct feature matches in all runs, N s is the number of matches satisfying the multiobjective fitness function condition in each run and Nr is the number of runs. |
| B. RMSE |
| RMSE will be closer to zero when the ground truth and automatic aligned images are similar and will increase when the dissimilarity increases. RMSE is defines as |
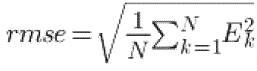 (19) (19) |
| Where E k is the difference between the pixel values for the ground image and automatic aligned image. N signifies the total number of pixels in the image. |
RESULTS AND DISCUSSION
|
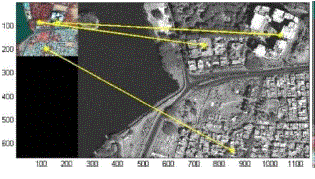
| Image set 1: The location is Ulsoor lake, Bangalore, India .The reference image is Quick Bird multispectral with a resolution of 2.4 m, and the sensed image is a OuickBird panchromatic resolution of 0.61 m. |
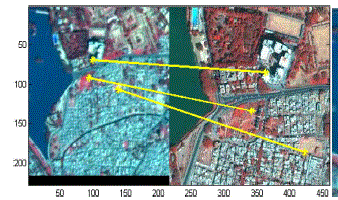
| Image set 2: The reference image is the same as that considered in Image set 1, while the sensed image is Linear Imaging Self-Scanning Sensor 4 with a resolution of 5.8 m. |
| A. Image set 1 |
| The corner points are extracted using modified using modified HCD. The corner points detected in the reference and sensed images were to be 40 and 62 respectively. The population size for the DPSO was fixed to ten particles, each containing a cluster of three points from the reference and sensed images as shown in (14) . Table 1 illustrates the number of matched points obtained by the selection of the different DPSO parameter values. In this table, we can observe that the number of matched points varies for different parameter values. The best number of matched points is obtained by setting the parameter values of α, β and γ to 0.6, 0.8 and 1 respectively . |
| between objective functions, and this leads to Pareto-optimal solution. The global set of matched points is three; hence, the threshold value (t1, t9) is set to (0.8, 5) or (1, 5) or (1, 4). This is where the threshold value is optimum and the number of matched points is assured. The global best vector which gives the best affine match points must contain three points that matches in the reference and sensed images (i.e., N = 3). The process is repeated for ten times (Nr. = 10). |
| Hence the feature correspondence was found to be 0.5 , whereas RANSAC fails to pick three matched points. The rmse value for the registered image using RANSAC was found to be 0.81 , while the value obtained using DPSO was found to be 0.81 , while the value obtained using DPSO was found to be equal to 0.29. |
CONCLUSION
|
| In this Paper, a new multi-objective optimization of the angle and distance conditions using DPSO based on switching technique has been proposed for feature matching. It is found that the proposed technique is able to register the sensed image with the reference image by matching the corner points obtained from the modified HCD. There are few restrictions in DPSO. The initial population is random, and the parameters are set empirically for better match. From the result obtained using both the case studies, DPSO is found to be better than RANSAC. |
| In the past, RANSAC and its variants were applied to match the points. Based on the result obtained, it clearly indicated that the proposed method is more efficient than RANSAC for multisensory image registration as it incorporates angle conditions besides the distance condition for feature matching. |
Tables at a glance
|
 |
 |
| Table 1 |
Table 2 |
|
| |
Figures at a glance
|
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 2a |
 |
 |
 |
| Figure 3 |
Figure 4 |
Figure 5 |
|
| |
References
|
- Z.BarbaraandF.Jan,“Imageregistrationmethods:Asurvey,”ImageVis.Comput.,vol.21,pp.977–1000,2003.
- V.W.Medha,M.P.Pradeep,andK.A.Hemant,“Imageregistrationtechniques:Anoverview,”Int.
J.SignalProcess.,ImageProcess PatternRecognition.,vol.2,no.3,pp.1–5,2009.
- B.Peter,L.Richard,andL.Frederic,“Anareabasedtechniqueforimage-to-imageregistration
ofmultimodalremotesensingdata,” inProc.IEEEInt.Geoscience.RemoteSens.Symp.,2008,pp.V-212–V-215.
- X.ZhangandC.Zhang,“Satellite cloud imageregistrationbycombiningcurvatureshape
representationwithparticleswarmoptimization,”J.Softw.,vol.6,no.3,pp.483–489,2011.
- M.A.FischlerandR.C.Bolles,“Randomsampleconsensus:Aparadigmformodelfittingwith
applicationstoimageanalysisandautomatedcartography,”Communication.ACM,vol.24,no.6,pp.381–395,Jun.1981.
- P.H.S.TorrandA.Zisserman,“MLESACAnewrobustestimatorwithapplicationtoestimatingimagegeometry,”
Comput.Vis.ImageUnderst.,vol.78,no.1,pp.138–156,Apr.2000.
- P.H.S.Torr,“AstructureandmotiontoolkitinMatlab—InteractiveadventuresinSandM,”MicrosoftResearch,MountainView CA,Tech.Rep.MSRTR-2002-56,2002.
- .V.RodehorstandO.Hellwich,“Geneticalgorithmsampleconsensus(GASAC)—Aparallelstrategyforrobust parameterestimation”inProc.Comput.Vis.PatternRecognition.Workshop,2006,p.103.
- G.Troglio,J.A.Benediktsson,S.B.Serpico,G.Moser,R.A.Karlsson,G.H.Halldorsson,andE.Stefansson,
“Automaticregistrationof retinaimagesbasedongenetictechniques,”inProc.30thAnnu.Int.IEEEEMBSConf.,2008,pp.5419–5424.
- M.K.KhanandI.Nyström,“Amodifiedparticleswarmoptimizationappliedinimageregistration,”in
Proc.20thInt.Conf.PatternRecog.,2010,pp.2302–2305.
- Y.Bentatau,N.Taleb,A.Bounama,K.Kpalma,andJ.Ronsin,“Featurebasedregistrationof
satelliteimages,”inProc.15thInt.Conf.Digit.SignalProcess,2007,pp.419 – 422.
- J.Senthilnath,S.N.Omkar,V.Mani,andT.Karthikeyan ,“Multi-objectiveoptimizationof
satelliteimageregistrationusingdiscreteparticleswarm optimization,”inProc.IEEEINDICON,2011,pp.1–5.
|