Multidimentional Motion Control of Robotic
Arm

Vansjaliya Kinjal; Prof. Tarun R. Dholariya; Dr. Charmy Patel

Multidimentional Motion Control of Robotic Arm

Vansjaliya Kinjal¹, Prof. Tarun R. Dholariya² and Dr. Charmy Patel³

Master Student, Dept.of E.C., GTU University, Rajkot, India
Assistant, Dept.of E.C., GTU University, Rajkot, India
Associate Prof, Dept.of E.C., GTU University, Rajkot, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Multidimensional motion control of robotic arm mainly use in industry and non-industry purpose. It helps to reduce the human work and increase the precision in work. Robotic arm provide similar function as human arm depending upon the degree of freedom it can offer. Motion control system of robotic arm needs several functions in order to perform the complex tasks required for industrial robots. These function include inverse kinematics, control signal generation and speed control. Degree of freedom get using inverse kinematics method, using this method complex computation of angle calculate. Most important part is controlling of robotic arm. Spartan-III FPGA is used for control the motion of robotic arm with the help of PWM signal. For different type of movement at different angle FPGA will control the motor through driver circuit, FPGA will generate PWM signals to guide the motor and accordingly different movements can be set.

Keywords

Spartan-III FPGA chip, servo motor, Inverse Kinematics, PWM signal, Xilinx VHDL.

INTRODUCTION

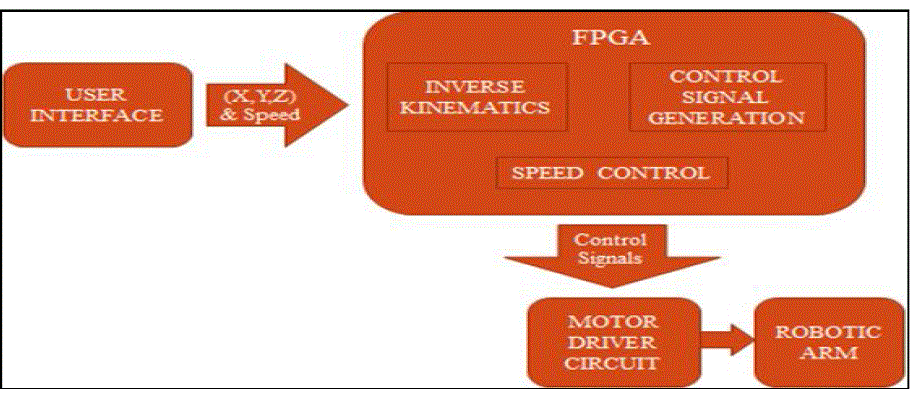
Robotic arm provides similar functions like a human arm depending upon the degree of freedom it can offer. Motion control system plays a major role in the control of different types of industrial automation devices such as robotic arm manipulator [1]. A multiple axis motion control system needs many functions in order to perform the complex tasks required for industrial robots very quickly and accurately. Arm controller is the challenging field in industrial applications. Robotic control is an exciting, complex and high challenge research work in recent year [2]. We are going to design the robotic arm controller using Spartan-III FPGA chip. Instead of DSP controller FPGA chip is widely used because of its simplicity, flexibility, low power consumption and high density. FPGA generate the motion control signals i.e. PWM motion control signal for controlling the robotic arm. In this paper use servo motor for drive the robotic arm. We are going to use the Spartan-III FPGA to control the servo motor. As a motor requires high voltage to operate so a PWM signal will not be able to drive it. Hence a driver circuitry is used to drive the motor [3]. This position information is send back to the FPGA controller so it knows how much farther the motor needs to be turned. In this paper robot consists of an arm with four degree of freedom (DOF). Entire system bounded by hardware and software design.

This paper represents several functions in order to accurately perform the complex tasks required for industrial robots. These include inverse kinematics, control signal generation and speed control. Conventional numerical approaches for these functions have complicated floating point computations. Complicated multiplication, addition, and trigonometric functions are needed to perform to calculate inverse kinematics. For the complex computation of inverse kinematics, IP core (intellectual property core) provided by Xilinx company is very useful which provides trigonometric functions and all floating point operations.

RELATED WORK

In paper [1], a multiple axis motion control chip was developed to control a multiple-axis motion system such as a robotic arm manipulator. This chip was designed using VHDL and implemented on an FPGA, thus allowing for a highly sampled, accurate, flexible, compact, low-power, and low-cost motion control system. In this paper it is given that velocity profile generation module, Interpolation calculation module and Inverse kinematics calculation module. Proposed multiple-axis motion control chip consists of an external interface, an interpolation calculator, an inverse kinematics calculator, a clock generator, a velocity profile generator, a pulse integrator, a feedback counter, a PID controller, and a data converter. The experimental results of this multiple-axis motion control system demonstrate that the proposed multiple-axis motion control chip has the performance that is required to efficiently perform the given task.

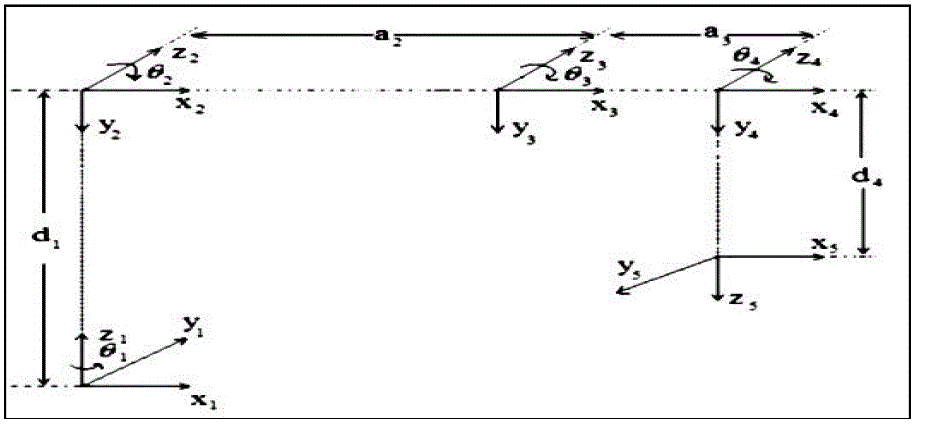
FPGA-based motion control IC allows a fully digital motion control for a five-axis articulated robot arm, such as inverse kinematic computation, point-to-point motion controller, position and velocity controller, PWM generation circuits are all integrated and realized in a single FPGA chip. the link coordinate system of a five-axis articulated robot using Denavit-Hartenberg convention. The kinematic parameters of Mitsubishi RV-M1 micro robot arm used in paper [2].

SYSTEM DESCRIPTION

A. FPGA controller

We are usingSpartan-III FPGA Chip as controller in our project. It is the main part of the system, through it all the motion of robotic system has to be control. A programmed FPGA will contain the VHDL code, which will correlate the inputs to the robotic arm movement. The FPGA system is flexible because it can be easily reconfigured and reused for many different applications of robotics. We are going to use the FPGAs to control the motor with driver circuit. FPGA controller is used to generate direction and the number of pulses required to rotate a robotic arm at given angle. The proposed control scheme has been realized using XILINX FPGA.

B. Signal generator

In our project we use PWM signal pulses for controlling purpose of the motor at require angle. Pulse width modulation also known as pulse duration modulation, where samples of the message signal are used to vary the duration of the individual pulses in carrier. But in our case message signal will be the position required for the motor shaft. The term duty cycle describes the proportion of on time to the period of time. Each motor have different PWM signal as per the motor requirement. PWM signal control the system movements and angles of the robotic arm.

C. Servo motor

Servo motors are very useful in the world of robotics because of its high torque and precise movements [4]. Servo motors work in a closed loop. The closed loop of a servo motor greatly increases the precision of the control system. In a servo motor the angles to which the shaft can turn to is limited only by the number of different PWM pulse widths that the FPGA system can supply.

A servo motor is an automatic device that provides motion control with the help of error-correction. The term ‘servo’ is used for the systems. It means a closed loop feedback mechanism means servo motor used for the position control. It combines AC/ DC motor and position sensor such as digital encoder.

In servo motor the potentiometer is used for position monitoring. Potentiometer is connected to gear of the servo motor, and is monitored by control circuitry. Control circuit monitors the potentiometer and determines the current motor angle and then it will compare with the required angle and will generate appropriate control signal to achieve the desired angular position. Generally servo motors provide angular motion between 0° and 1800°.

INVERSE KINEMATICS CALCULATION

A. Inverse Kinematics

The transformation of the position and orientation of a manipulator end-effector from Cartesian coordinates to joint coordinates is known as the inverse kinematics problem [5]. Robotic arm control actions are described in the form of end effector Cartesian coordinates, but here use motor, motion of the arm has to be done in angular form. So conversion of Cartesian coordinates into joint angles is needed, and it can be done by inverse kinematics. To solve the inverse kinematics problem number of methods and there combinations used. Each method has its own advantages and disadvantages, so, as per the requirement combine them together. Main methods of inverse kinematics problem solution are Algebraic methods and Iterative methods. In this paper use Algebraic method to calculate the angles of joints corresponding to a given coordinates of the tip of the robotic arm.

B. Angle equations

The inverse kinematics of the articulated robot manipulator will transform the coordinates of robot manipulator from Cartesian space R³ (x,y,z) to the joint space R4 (θ1, θ2, θ3, θ4).

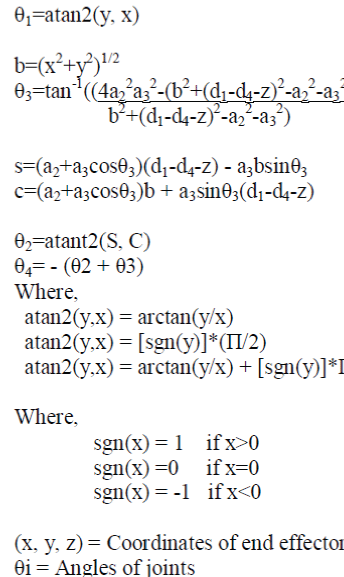FLOATING POINT

Floating point representation has several advantages over fix point representation. Floating point number supports wide range of values because of that we get accurate and precise result.

Floating point represent with various numbers of bits. Floating-point representation - the most common solution - basically represents real number in scientific notation. Floating point number is expressed in the scientific notation, with a fraction, and exponent of a certain radix [6]. Set the sign bit, 1 for negative, 0 for positive, according to the sign of original number.

A. Single precision floating point

Single precision floating point numbers are represented by 32 bits per number. Floating point numbers supports wide range of values.

Exponent range is: [-128 , 127]

Approximate range is: 10^-38 to 10³⁸

B. Example of single precision floating point

Let us try and represent the decimal number (9.5)10 in IEEE floating-point format. Steps:

• Binary representation of the operand: 1001.1

• Normalized representation of the operand: 1.0011× 2³

• Sign bit = 0

• Biased exponent: 127+3 = 13010 = 100000102

• Mantissa = 00110000000000000000000

• IEEE representation of the operands:

• A = 0 10000010 00110000000000000000000

INTELLECTUAL PROPERTY (IP) CORE

For the complex computation of Inverse Kinematics and Interpolation, IP core provided by Xilinx Company is very useful which provides trigonometric functions and all floating point operations. These are the functions already created by Xilinx to provide their users ease of programming, coding of which cannot be edited. IP core is a reusable unit of logic and can be used as building blocks in chip or logic design.

There are some mathematical operations which are required to perform complex mathematical equations, for example, trigonometric functions and square root of the number etc. There are mathematical functions and logical functions available as IP cores.

SIMULATION RESULTS

Trigonometric function and multiplication, addition, subtraction etc. are use in angle simulation result. Here use Xilinx IP core and VHDL programming language for simulation.

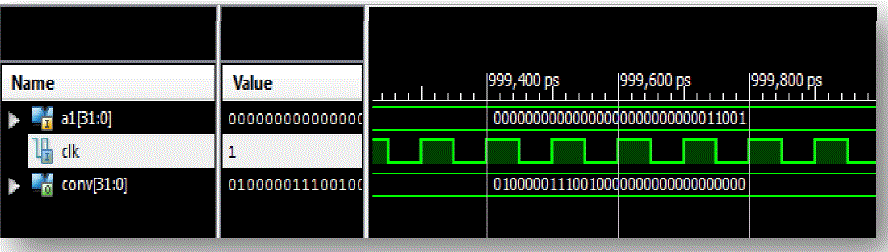
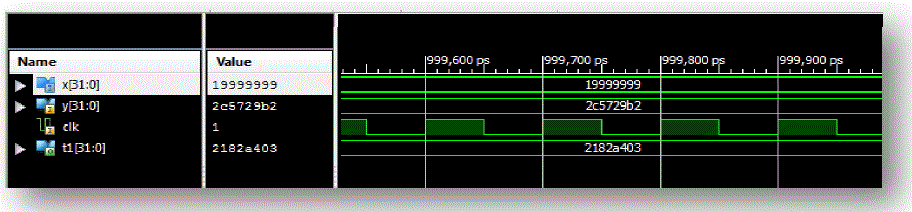
Figure 4 shows the simulation result of conversion from fix point to floating point. Here real number is 25.

Figure 5 shows the floating point multiplication here the number which multiplies are 12 and 3, and get the multiplication result 36 in floating point format.

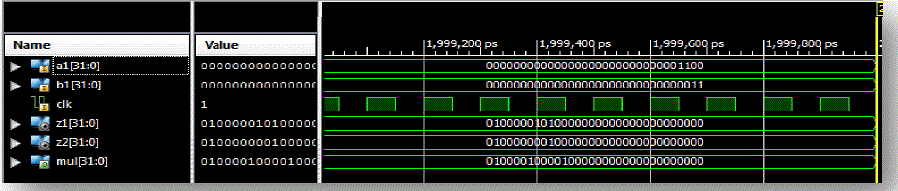
Figure 6 and 7 represent the trigonometric function in floating point format.

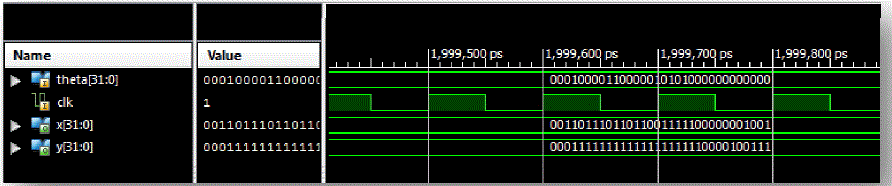
Figure 8 shows the atan2 function which is useful for angle equation simulation.

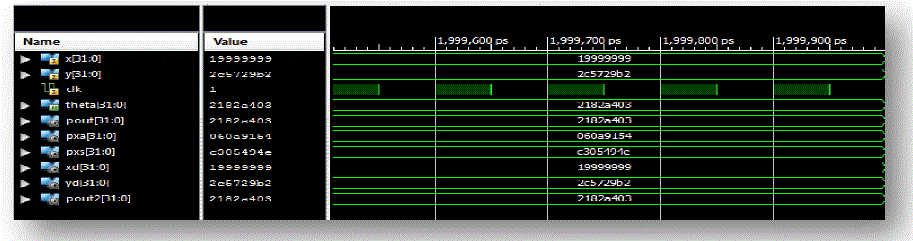
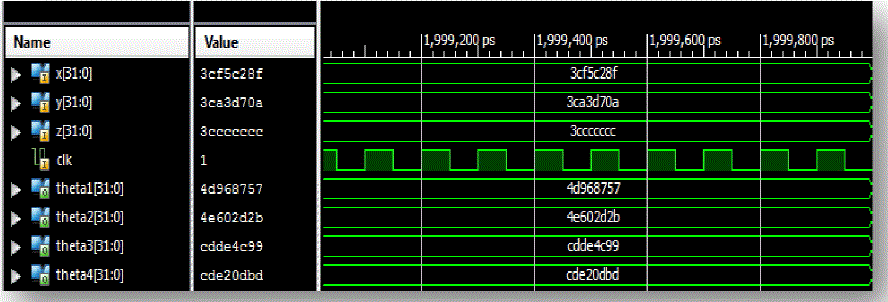
Figure 9 shows the simulation result of robotic arm angle equations in single precision floating point format. Here single precision floating point format use for the angle calculation because using this format we get accurate and precise angle equation.

CONCLUSION

With the help of simulation for all the angles, it is concluded that for the input width of 32 bits of coordinates, precision of 32 bits is achieved. Speed control of the robotic arm can be achieved by changing the frequency of PWM signal for every motor on every joint.

Figures at a glance


Figure 1	Figure 2	Figure 3	Figure 4	Figure 5

Figure 6	Figure 7	Figure 8	Figure 9

References

Jung Uk Cho, Quy Ngoc Le, and Jae WookJeon “An FPGA-Based Multiple-Axis Motion Control Chip” IEEE Trans. Ind. Electron., Vol. 56, NO.3, March 2009.

Ying-Shieh Kung, Gua-ShiehShu, “Development of a FPGA-based Motion Control IC for Robot Arm”, pg.no. 1397 to1402, IEEE 2005.

Mrs. UrmilaMeshram (Thulkar), Mr. pankajBande, Mr. P.A. Dwaramwar, and Mrs. R. R. Harkare, “Robot Arm Controller Using FPGA”, IEEEimpact2009.

VivekRamakrishnan, NalamwarSanchitGopal, Rahul Ashok and S. Moorthi, “FPGA based DC Servo motor Control for Remote Replication ofMovements of a Surgical Arm”, IEEE 2011, pg.no.671-675.

AddankiPurna Ramesh, Rajesh Pattimi, “High Speed Double Precision Floating Point Multiplier”, International Journal of Advanced Research inComputer and Communication Engineering, Vol.1,Issue 9, November 2012.

P. Gayatri, P. Krishna Kumari, V. Vamsi Krishna, “Design of Floating Point Multiplier Using Vhdl”, International Journal of Engineering Research and Development, Vol. 10, Issue 3, March 2014.