Keywords
|
| Systematic Code; Coding Efficiency; Parity Bit; Weight of a code word; Random Error; Burst Error; Component Code; Error Vector;MATLAB. |
INTRODUCTION
|
| Error Control Coding or Channel Coding Technique provides various ways of implementing Shanon?s Channel Coding Theorem. Channel coding is used to facilitate the reliable transmission over the communication channel. Error Correcting Codes are classified into Block Codes and Convolutional Codes. In Block Codes, the Channel encoder encodes a block of “k” message bits, into a block of “n” coded bits by appending redundancy of “r = n-k” parity bits, to each “k” bit message word, resulting an (n, k) Block Coded word. Thus, in an (n, k) block code, each “k” bit data/message word is mapped to an “n” bit code word, with a unique mapping. In a Binary Code, each data word and Code word are constituted by the alphabets 0 and 1. The code word length “n” is given as where “t” is the number of errors that are corrected by the respective (n, k) Block Code. The “r” number of parity bits are obtained as the linear combination of Message bits. In a Linear (n, k) Block Code, any two code words of the code are Modulo-2 added to produce the third code word of the code. In a Systematic code, the message bits are transmitted in unaltered form. The code efficiency or code rate of an (n, k) Block Code is given by which is always, less than 100%. |
| Due to the noise in the communication channel, the transmitted bit may be wrongly decided at the receiver and all such wrong decisions are referred to as errors. These may occur randomly i.e. random errors or in the form of Bursts, i.e. Burst errors, or a combination of the two. Hence, it is desirable to have codes that are capable of correcting random errors as well as Burst errors. This paper proposes a Multiple error correcting coding scheme, capable of correcting random errors as well as Burst errors. |
II.WEIGHT BASED CODES
|
| The encoding of a Message Word depends on the weight of the message word and hence, these codes are referred to as “Weight Based Codes”. These are 1-Dimensional Codes (n, k) codes, and are of 50% coding efficiency. Unlike the linear Systematic Block Codes, the parity bits in each code word of the proposed codes are not the linear combination of message bits. The parity bits of the code word are selected depending on the weight (No. of 1?s) of the message word. Thus, unlike (n, k) Systematic Linear Block Codes, the parity bit structure of all the code words of the proposed coding scheme is not the same. Hence, these codes are also referred to as ”Codes with Unequal Parity Bit Structure”. These are single error correcting codes. |
A.Encoding:
|
| The general form of an (n, k)Weight Based code word is given by [ M1M2M3……..MK P1P2P3…..PK], where M1,M2,M3 …..,Mk are 'k' message bits and P1,P2,P3, …..,PK are the (n-k) number of parity bits where n=2k. The un-coded message word is [ M1M2M3……..MK ]. |
The encoding rule is
|
| For the message word with Zero weight /Even weight, the parity bits of the corresponding code word are same as the message bits. |
| For the message words with odd weight, the parity bits of the corresponding code word are the complements of the message bits. |
B.Error Detection and Correction:
|
| Let the received Code word be |
 |
| where 1,2,3… indicate the bit positions in the received code word. All Mi 's and Pi &s, =1,2,- -,k represent the „k no. of data bits and k no. of parity bits respectively. The length of the code word is n=2k bits. |
| Under error free reception, each received code word R satisfies the following conditions: |
Condition1:
|
For the received code word, whose parity bits are same as the message bits , there will be k no. of conditions given as  |
| For the received code word, whose parity bits are the complements of message bits, there will be k no. of conditions given as |
 |
Condition2:
|
| For the received code word, whose parity bits are same as the message bits, there will be 2k conditions given as: |
 |
| For the received code word, whose parity bits are complements of the message bits, there will be 2k conditions given as: |
 |
| Any deviation from the above error free conditions indicates the reception with error/errors. |
| Due to the additive noise, in general , the received code-word R differs from the transmitted code-word C, by the error pattern E i.e. R=C+E. The error pattern or the error Vector E is a [1xn] row vector for an (n, k) Component code. Under Error free reception, it is an all zero vector. |
| The error vector is computed from the decoding process which involves the following steps: |
1)Verifying the structure of the Parity Bits:
|
| The Parity bits of the received code word are Modulo-2 added with the Message bits, i.e. |
 |
| The structure of the Parity bits can be decided based on the above Modulo-2 added sum. |
| If the parity bits of the code word are same as message bits, the above Modulo-2 sum consists of (i) all zeros, under error free reception. (ii) (k-1) number of 0?s and a single 1, under reception with error |
| If the parity bits of the code word are the complements of message bits, the above Modulo-2 sum consists of (i) all ones, under error free reception(ii) (k-1) number of 1?s and a single zero, under reception with error. |
| 2)Checking the Position of the Error: |
| After deciding about the structure of the Parity bits,the „k? number of summations in Condition-1 are applied to the received code word. |
| If any of these „ k? number of summations applied for the received code word is differing from the error free condition, it can be concluded that the corresponding Mi or Pi of that sum will be in error. |
| 3) Identifying the Error Location: |
| The error location can be identified by using the?2k? number of summations in Condition-2. |
| After estimating the error position in the received code word i.e. after identifying the bit pair (Mi, Pi) in which, any one can be in error, the above?2k? summations are made into two groups such that GROUP-1 contains „k? summations that do not involve Pi and GROUP-2 contains „k? summations that do not involve Mi. One of the above two groups that is differing from the error free conditions is considered as the group containing the bit which is in error. |
| The bit ( eitherMior Pi) which is commonly present in all the summations in the above selected group will be the bit in error in the received code word. |
| The corresponding Error Vector E will be an [1xn] row vector, consisting of a “1” in the bit Mior Pi, depending on the bit which is found to be in error. The corrected Code word is C=R+E .In other words, the error in the received code word is corrected by complementing the respective error bit. |
III. MULTIPLE ERROR CORRECTING CODES
|
| These codes are capable of correcting Burst errors and multiple number random errors.These proposed codesare(3k, k) two-dimensional codes, used for the message words of even length, and each code array is constructed using a (6,3)Weight Based Code, as the component code. Each code word is a [6, 2 ] rectangular array consisting of 3k elements. These codes are having a coding efficiency of 33.33%. |
| A.Encoding |
| 1) Method-1: |
| Let M1 M2 M3 − − M be the k(even) bit data word. The proposed Multiple Error correction code is a two dimensional code array, whose first two rows consists of first k/2 and second k/2 bits of the data word, respectively. The third row of the array is thebit by bit |
| Modulo-2 sum of the first two rows. Thus, the first three rows of the code word are |
 |
| Each column of the above array is encoded using (6,3) weight based code as a component code. The First two rows of the array represent the actual data word. |
| 2)Method-2: |
| Let M1 M2 M3 − − M be the k(even) bit data word. The proposed Multiple Error correction code is a two dimensional code array, whose first two rows consists of first k/2 and second k/2 bits of the data word, respectively. The third row of the array is thebit by bit |
| Multiplication of the first two rows. Thus, the first three rows of the code word are |
 |
| Each column of the above array is encoded using (6,3) weight based code as a component code. The First two rows of the array represent the actual data word. |
| 3) Multiple Error detection and Correction:The code word is transmitted row by row, with the 6th row being the first and 1st row in the last, i.e. the last row will be |
 |
| The received code word is arranged back into an array on a row by row basis. The random errors can be detected and corrected using column correction. The received code word with any error burst of length “k/2” or less, in any row , or “k/2” number of random errors, one error in each column will be corrected by column decoding. |
IV. ILLUSTRATION
|
| 1. Let the data word be 1011, which is of length 4 bits. |
Encoding:
|
The first two rows of the code array will be 1 0 1 1 .the first three rows of the code array will be 1 0 1 0 1 1 . Then each column of the array is encoded using (6,3) Weight Based Code. Hence, the code array for the Data Word 1011 will be 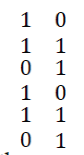 |
If the encoding is using Method-2, the third row of the array will be the bit by bit multiplication of the first two rows. Thus, the first three rows of the code array will be 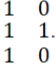 Then each column of the array is encoded using (6,3) Weight Based Code. Hence, the code array for the Data Word 1011 will be Then each column of the array is encoded using (6,3) Weight Based Code. Hence, the code array for the Data Word 1011 will be 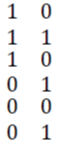 |
Decoding:
|
| Let the code array be generated using Method-1 and the received code array be |
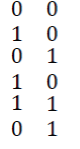 |
| Error Detection and Correction is done column wise. |
| Consider the first column of the received code array, written as |
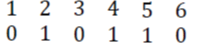 |
Where, 1,2,3,---etc, represent the bit positions.
|
|
The bits in the positions 4,5, and 6 are Modulo-2 added with the Bits in the positions 1,2 and 3 i.e.
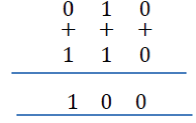
|
| The above Modulo-2 added sum of length 3 is consisting of a single „1? and 2 number of 0?s.This indicates that the bits in positions 4,5 and 6 are same as the bits in the positions 1,2 and 3.Under the reception without error, the above Modulo-2 added sum should contain all Zeros. Since the bits in the positions 1 and 4 are modulo-2 added to give a 1, and that sum is differing from the error Free condition, it can be concluded that either the bit in position 1 or 4 of the 1st column of the received code array is in error. |
| Among 6 number of conditions under error free reception(Condtion-2), the conditions that do not involve the bit in position 1 and the conditions that do not involve the bit in position 4 are made into two groups. |
| Under Error Free reception, these summations will be as follows: |
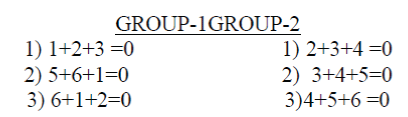 |
| Where, the above Modulo-2 operations are applied for the bits available in the positions as indicated. |
| The above summations applied for the 1st column of the received code array are |
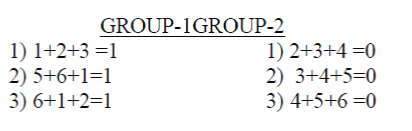 |
| Since the Summations in Group-1 obtained are differing from error free conditions, this group is considered as the group consisting of the bit which is in error. Since, the bit position 1 is commonly present in all the summations in Group-1, it can be concluded that the bit in position 1 of the 1st column of the received code array is in Error. The corresponding Error Vector is E= 1 0 0 0 0 0 0. Hence the corrected column is 1 1 0 1 1 0. |
| Consider the secod column of the received code array, written as |
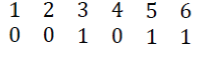 |
Where, 1,2,3,---etc, represent the bit positions.
|
| The bits in the positions 4,5, and 6 are Modulo-2 added with the Bits in the positions 1,2 and 3 i.e. |
 |
| The above Modulo-2 added sum of length 3 is consisting of a single „1? and 2 number of 0?s.This indicates that the bits in positions 4,5 and 6 are same as the bits in the positions 1,2 and 3.Under the reception without error, the above Modulo-2 added sum should contain all Zeros. Since the bits in the positions 2 and 5 are modulo-2 added to give a 1, and that sum is differing from the error Free condition, it can be concluded that either the bit in position 2 or 5 of the 2nd column of the received code array is in error. |
| `Among 6 number of conditions under error free reception(Condtion-2), the conditions that do not involve the bit in position 2 and the conditions that do not involve the bit in position 5 are made into two groups. |
| Under Error Free reception, these summations will be as follows: |
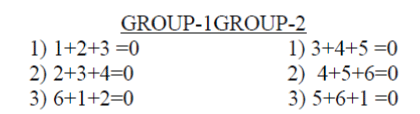 |
| Where, the above Modulo-2 operations are applied for the bits available in the positions as indicated. |
| The above summations applied for the 2nd column of the received code array are |
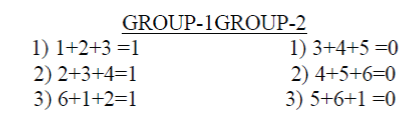 |
| Since the Summations in Group-1 obtained are differing from error free conditions, this group is considered as the group consisting of the bit which is in error. Since, the bit position 2 is commonly present in all the summations in Group-1, it can be concluded that the bit in position 2 of the 2nd column of the received code array is in Error. The corresponding Error Vector is E= 0 1 0 0 0 0 0. Hence the corrected column is 0 1 1 0 1 1. |
| Thus, the corrected code array is |
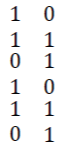 |
| Thus, two errors present in the received code array are corrected, and the data word is 1011, available in the first two rows of the code array. |
V.WEIGHT ENUMERATORS AND PROBABILITY OF UNDETECTED ERROR
|
| Weight of a code word is the number of 1?s available in it. Undetected errors occur only when the decoder fails to detect the presence of errors. If the coding scheme is used only for error detection on a Binary Symmetric Channel, the probability of an undetected error Pud (E) can be computed from the weight distribution {Ai} of the Code. |
If the code “C” contains Ai number of code words of weight “i”, the weight Enumerator A(z) of the code “C” is defined as 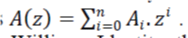 |
Using MacWilliams Identity, the probability of undetected error can be computed from the Weight Enumerators A(z) of the code “C”. It is given as 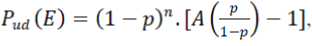 for the Weight Enumerator of the code for the Weight Enumerator of the code 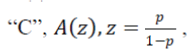 where “p” is the transition Probability (probability that a transmitted “0” is received as “1” and vice versa) and “n” is the number of code bits in the code word. Consider a (12,4)Multiple Error Correction Code, generated using Method-1. where “p” is the transition Probability (probability that a transmitted “0” is received as “1” and vice versa) and “n” is the number of code bits in the code word. Consider a (12,4)Multiple Error Correction Code, generated using Method-1. |
The set of weight distributions of the code is {A0, A4, A8} = 1,6,9 , i,e. number of code words with zero weight=1; number of code words with weight Four=6; number of code words with weight Eight=9. The Weight Enumerator of the code is 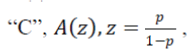 |
| The Probability of undetected error is given as |
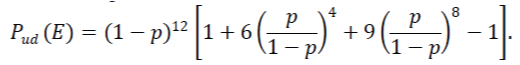 |
| Consider a(12,4) Multiple Error Correction code,generated using Method-2 .The set of weight distributions of the code is{A0, A3, A6} = 1,6,9 , i,e. number of code words with zero weight=1; number of code words with weight Three=6; number of code words with weight Six=9. |
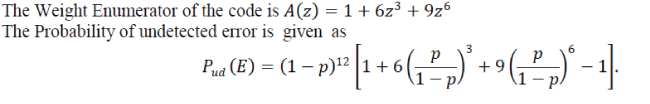 |
| The computations for different transition probabilities (p?s) are tabulated in Table1. |
| i.e. for example, for a transition Probability of 10-3, over a Binary Symmetric Channel, above pud(E) tells that, for the Multiple Error Correcting Code generated using Method-1 , out of 1012 code digits, there are on average 6 erroneous digits that pass through the decoder undetected and for a the Multiple Error Correcting Code generated using Method-2, out of 108 code digits, there are on average 6 erroneous digits that pass through the decoder undetected . |
VI.PROBABILITY OF ERROR CALCULATIONS FOR THE PROPOSED CODES
|
With no coding applied, the Probability of bit Error in the un-coded bit stream is 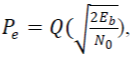 where Eb = where Eb = is the average bit energy and N0 is the Noise Power Spectral density. is the average bit energy and N0 is the Noise Power Spectral density. |
| The Message Error Probability is given as 1 − (1 − pb)k where k is the length of the message word. Consider a binary source with a bit rate of 104 bits/sec and the channel be an additive White Gaussian Noise Channel. Let the received power is 1μw and the Noise Power Spectral Density N0 2 = 10−11w/Hz. Assume Antipodal Signaling. |
| The respective bit error probability values,Pb = 7.827 * 10−4. Considering that the Message Word is consisting of 4 bits, the message Error Probability is given as Pe = 1 − 1 − Pb 4 = 0.0031. |
| For the Coded bit stream, under „Antipodal? signaling, assuming equi-probable messages ,the Message Error |
 |
VII. CONCLUSION
|
| The proposed Weight Based Codes are Single Error Correcting Codes and the proposed Multiple error Correcting codes are capable of handling the random errors and Burst Errors also and they are with a coding efficiency of 33.33%. |
| The Multiple Error Correcting Coding Scheme using Method-1 is found to have better error performance than that using Mehod-2 . From Fig.8.1., it can be found that for an Eb/N0 of 7.16dB, the BER for the proposed code using Method-1 is 0.0981*10−3 and for the proposed code using method-2, it is 0.6301*10−3 .Hence, it can be concluded that, for a given BER, code suing Method-1 provides a better coding gain, relative to the Code using Method-2 and the Overall BER is better in the code using Method-1 relative to the other. |
| The existing (10,4) Linear Binary Block Code with 40% coding efficiency is also a double error correcting code, and corrects only random errors. Even though the prosed (12,4)code is of less efficiency(33.33%), it can correct random as well as Burst errors also. |
| Similar conclusion can be made while comparing (15,8) Double error correcting Linear Block Code. The proposed code for a message word of length 8 bits is (24,8), can correct 4 random errors or an error burst of length less than or equal to 4. |
| Thus, the error correcting capability of the proposed codes are comparably better when compared to the existing Linear Binary Block Codes. |
Tables at a glance
|
 |
| Table 1 |
|
| |
Figures at a glance
|
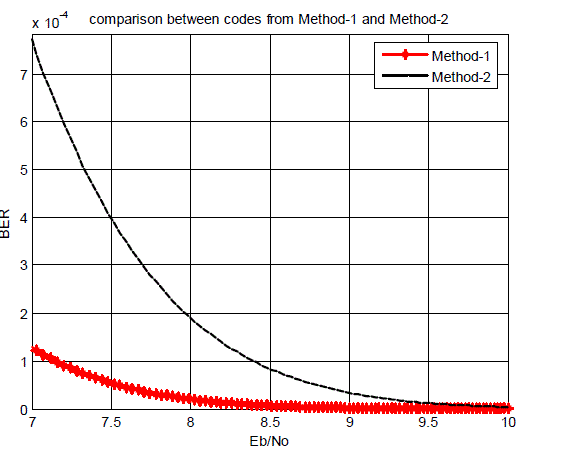 |
| Figure 1 |
|
| |
References
|
- Abraham Lempel,&ShmuelWinograd (July 1977).-“A New Approach to Error Correcting Codes”- IEEE Trans. Inform. Theory, vol. IT- 23,No.4, pp.505-508.
- Andrew j.Viterbi,&JimK.Omura(1979)-“Principles of Digital Communication andCoding”- McGraw-Hill International Edition
- BernardSklar(2001)-“Digital Communications-Fundamentals &Applications”-Pearson Education Asia
- F.J.MacWilliams&N.J.A.Sloane(1977)-“The Theory of Error-Correcting Codes”- North Holland Publishing Company
- Graham Wade(1994)-“Signal coding and Processing”, Cambridge University Press
- HaroldP.E.Stern, &Samy A. Mahmoud(2004)- “Communication Systems-Analysis and Design”, Pearson Education.
- John G.Proakis, MasoudSalehi(2002)- “Communication Systems Engineering” , 2nd Edition, Pearson Education Asia
- Man Young Rhee(1989)- “Error Correcting Coding Theory”-McGraw- Hill publishing Company
- Richard.E.Blahut(Nov.1977)-“Composition Bounds for Channel Block Codes”, IEEE Trans. Inform.Theory Vol.IT-23,No.6,pp.656-674.
- ShuLin,Daniel&J.Costello,JR(1983)-“Error Control Coding-Fundamentals and Applications” Prentice –Hall,Inc.Englewood Cliffs, New Jersy 07632
- P.SriHari&Dr.B.C.Jinaga(2007)-“DATA INVERTING CODES”-Ph.D Thesis, Jawaharlal Nehru Technological University, Hyderabad, India.
|