Nijenhius Tensoron Hyperbolic Hsu-Structure
Manifold

Lata Bisht; S; hana Shanker

Nijenhius Tensoron Hyperbolic Hsu-Structure Manifold

Lata Bisht¹, Sandhana Shanker²

HOD, Department of Applied Science, BTKIT, Dwarahat, Almora, Uttarakhand, India
Assist.Professor, Department of Applied Science, BTKIT, Dwarahat, Almora, Uttarakhand,India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Scope of this paper is to express the Nijenhius Tensor in various forms in Hyperbolic Hsu-Structure manifold. Firstly Hyperbolic Hsu-Structure manifold has been studied and discussed by Dr. R.S. Mishra [3], [4] and some of the great geometricians have also done work in Nijenhius Tensor in different differentiable manifold structures [5], [6], [7], [9]. In this paper, we have taken even dimensional differentiable manifold Vn(n = 2m) of differentiability class C ∞, where we have definedthe Nijenhius Tensor in Hyperbolic Hsu-Structure manifold and the decomposition of the Nijenhius Tensor in Hyperbolic Hsu-Structure has been done. And some of its properties have also been discussed. Similarly the decomposition of the associate Nijenhius Tensor and its properties in Hyperbolic Hsu-structure manifold has been discussed.

Keywords

Hyperbolic- Hsu structure manifold, Nijenhius Tensor, HGF-structure

I. INTRODUCTION

Proof: Interchanging X and Y in equation (2.1b), we get (2.2a), which shows that N is Skew-Symmetric in X and Y. Barring equation (2.1b) and applying structure we get equation (2.2c). Barring X and Y separately in equation (2.1b) and using structure in the two equations and then comparing the resulting equation we get (2.2b). Barring equation (2.2b) throughout and using structure in the resulting equation, we get the equation (2.2d). Barring X and Y in equation (2.1b), using structure and comparing the resulting equation with the equation obtained by multiplying equation (2.1b) by we get the equation (2.2e), which shows that N is pure in X and Y. Barring equation (2.2e)and using structure, we get the equation (2.2f). The equation (1.3a) is obtained from the equations (2.2d) and (2.2e). The equation (2.2c) and (2.2f) yield the equation (2.3b).

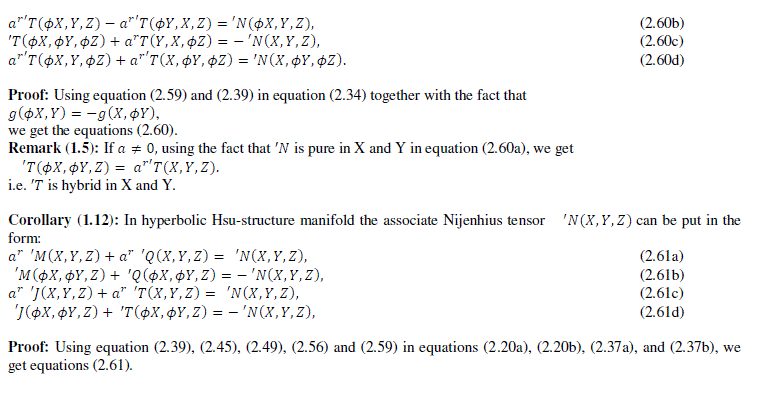References

Duggal,K.L "On Differentiable structure defined by Algebraic Equation, Nijenhius tensor", Tensor, N.S., Vol. 22, pp. 238-42, 1971.
Yano, K. "Differential Geometry on Complex and almost complex spaces", New York, 1965.
Mishra, R.S. "On almost Hermite spaces II, Nijenhius tensor", Indian J. Math. 9, pp. 161- 68, 1967.
Mishra,R.S. "Structures on a Differentiable manifold and their applications", Chandrama Prakhashan Allahabad, 1984.
S.B. Pandey and B.C. Joshi, "Hyperbolic General Differentiable manifold", Jour. Sci. Res., 9(1), pp. 43-44, 1987.
S.B. Pandey and Lata Bisht, "On Hyperbolic Differentiable Structure, Nijenhius Tensor", J. Nat. Acad. Math.Vol. 23, pp. 35 - 40, 2009.
Dr. Lata Bisht, "On Hsu-Structure Manifold, Nijenhius Tensor", International Journal of Advancements in Research and Technology, Volume 2, Issue 8, pp. 87 - 96,2013.
S. Kobayashi and K. Nomizu, "Foundation of Differential Geometry", Vol.I and II, Interscience Publisher, London.
R.D.S. Kushwaha and D.K. Yadav "On almost paracontact metric manifold:Nijenhius Tensor", Indian J of pure Appl. Maths, 13(6), pp. 633-636, 1982.