Node Localization in Wireless Sensor Network
Under Non-Line-Of-Sight Scenario

R.Divya; R.Gunasundari

Node Localization in Wireless Sensor Network Under Non-Line-Of-Sight Scenario

R.Divya, R.Gunasundari

PG Scholar, Dept. of ECE, Pondicherry Engineering College, Pondicherry, India
Associate Professor, Dept. of ECE, Pondicherry Engineering College, Pondicherry, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Localization is the process through which each of the sensor nodes determines its own position by itself. Obstacles blocking between the nodes is Non Line Of Sight (NLOS). Localization algorithms are used to estimate the node positions in wireless sensor networks (WSNs). It is an important research topic because position information is a major requirement in many WSN applications. In the latest literature, localization of NLOS error is carried out using Semi-Definite Programming (SDP). In the proposed work, Range Map Stitching (RMS) algorithm is used which overcomes the disadvantages of SDP. This method can provide good localization accuracy by mitigating the effects of NLOS measurements.

Keywords

non-line-of-sight; received signal strength; range map stitching; wireless sensor networks

INTRODUCTION

At present, wireless sensor networks (WSNs) have widely been applied in many fields, such as military needs, industry applications and environmental monitoring. One of the main challenges for accurate node localization in range-based localization algorithms is NLOS propagation due to obstacles blocking the direct paths of anchor signals.

Node localization in WSN has been literature surveyed under various paradigms. GPS information is exploited for few nodes and hence, the sensor nodes which know its position are called anchor nodes/reference nodes/beacon nodes/seed nodes/locationaware nodes. The sensor nodes which are not aware of their position are called sensor nodes/blind nodes/location-unaware nodes.

Consider both the sensor and the anchor nodes are static. The location estimates can be determined by Range-based (ToA, TDoA, RSS or AoA) or Range-Free (connectivity or hop count) techniques. The absolute coordinates of sensor nodes can be obtained by combining the location estimates by Anchor-based or Anchor-free algorithmic approaches. Hence, algorithmic approach is the best way for node localization. .Many algorithms are proposed, but it is still difficult to node location estimation accurately and efficiently in WSN since the proposed algorithm should be low complexity and to reduce the communication cost for WSN.

PROPOSED METHOD

`A. Distance Estimation

The RSS based localization techniques eliminate the need for additional hardware, and exhibit favorable properties with respect to power consumption, size and cost. In general, the RSS based localization techniques can be divided into two categories: the distance estimation and the RSS profiling based techniques.

In free space, the received signal strength at a receiver is given by the Friis equation:

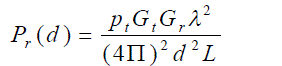Where Pt is the transmitted power, Pr(d ) is the received power at a distance d from the transmitter, Gt is the transmitter antenna gain, Gris the receiver antenna gain, L is a system loss factor not related to propagation and λ is the wavelength of the transmitter signal.

The gain of an antenna is related to its effective aperture, Ae, by

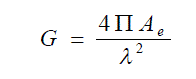(2) The effective aperture Ae is determined by the physical size and the aperture efficiency of the antenna. In a real environment, the propagation of an electromagnetic signal is affected by reflection, diffraction and scattering. Moreover, the environment will change depending on the particular application (e.g., indoor versus outdoor). However measurements have shown that at any value of d, the received signal strength Pr (d) at a particular location is random and distributed log-normally about the mean distance-dependent value.

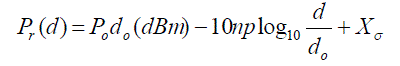(3) where Po (do) [dBm] is a reference power in dB milliwatts at a close-in reference distance do from the transmitter, np is the path loss exponent which indicates the rate at which the received signal strength decreases with distance and the value of np depends on the specific propagation environment, Xσ is a zero mean Gaussian distributed random variable with standard deviation σ and it accounts for the random effect of shadowing. The notation [dBm] denotes that power is measured in dB milliwatts units. If not, it is measured in watts.

The log-normal model has been extensively used to obtain the received signal strength. The reference power Po (do) [dBm] is calculated using the free space Friis equation or obtained through field measurements at distance do.

Based on above equation, it is trivial to show that given the received signal strength measurement, Pij, between a transmitter i and a receiver j , a maximum likelihood estimate of the distance, dij, between the transmitter and the receiver is:

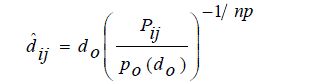(4) It should be noted that Pij and Po (do) are measured in watts instead of dB milliwatts.

B. Position Estimation

Range Map Stitching is used to estimate the coordinates of the blind sensor nodes. One method of fusing the precision of centralized schemes with the computational advantages of distributed schemes. Range Map Stitching (RMS) is a different way of approaching the same problem.

The RMS algorithm works as follows:

Step 1: Split the network into small overlapping maps. Very often each map is simply a single node and its onehop neighbors.

Step 3: Finally, merge the sub regions using a coordinate system registration procedure.

Let the node responsible for each local map chooses an integer coordinate system ID at random.

Each node communicates with its neighbors; each pair performs the following process.

Nothing should be done if both the ID same. If they have different IDs, then register the map of the node with the lower ID with the map of the node with the higher ID. Afterwards, both nodes keep the higher ID as their own. Repeat step 2 until all nodes have the same ID; now all nodes have a coordinate assignment in a global coordinate system.

C. NLOS Mitigation using RMS Algorithm

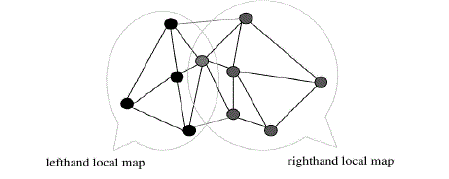
In the proposed work process of ML and MR be two local maps are to be stitched. ML and MR are the left-hand and the right-hand maps, respectively.Let li, i= 1,… nL , rj, j=1,…. nR denote the coordinates assigned to the nodes of the left hand and the right-hand maps, respectively.

Coordinates represents as 2D column vectors. Sometimes apply set operations to the maps. The purpose of the map-to-map stitching procedure is to find a transformation that translates, rotates, and/or reflects the right-hand map as a whole so that the resulting coordinates best meet the distance constraints.

Two types of distance constraints exist: 1) if a node is common to both maps, the left-hand coordinate and the transformed right-hand coordinate of the node must be as close as possible, and 2) if distance estimate d(u,v) is available for a member of ML and a member v of MR, their coordinates must match this distance as closely as possible after the transformation.

Suppose that there are m ≥ 3 common nodes between two maps. May assume without loss of generality that each pair (li,ri), i= 1,…m refers to two coordinates of the same node. The goal of the absolute orientation method is to find a translation vector t ε IR2 and a rotation/reflection matrix Q ε IR2X2 that minimize the sum of the squared error.

The stitching phase (step 3 above), uses coordinate system registration in a peer-to-peer fashion to shift all the local maps into a single coordinate system. One way of performing this stitching is described below:

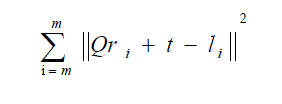(5) The error is minimized when the centroids of the common nodes in both maps coincide after the transformation.

RESULTS

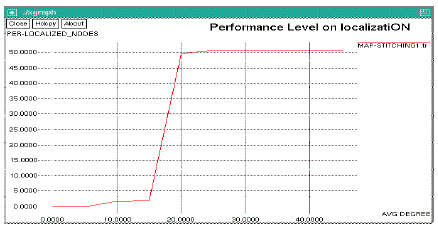
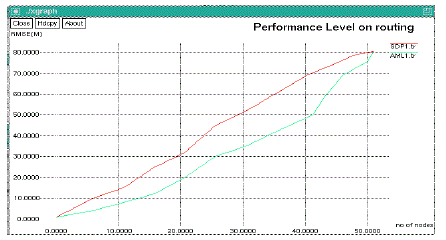
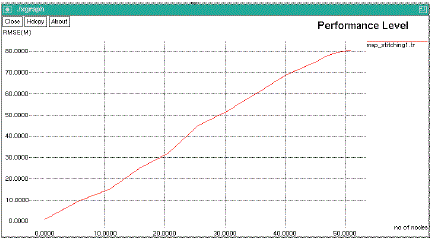
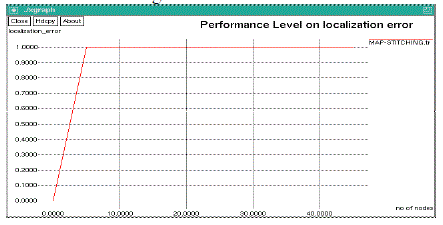
The map stitching is a type of localization algorithm in which the network is divided into small overlapping sub regions, each of which creates a local map, and then the local maps are stitched together to form a single global map. The proposed method achieves a better localization accuracy of static anchor nodes and static blind nodes under NLOS conditions.

CONCLUSION

Node localization based Range Map Stitching algorithm has been proposed. Simulation results demonstrate the effectiveness of our method. With the great success of the GPS, position-based applications have attracted more and more attention, not only in outdoor open areas, but also in indoor environments. Many localization algorithms are proposed, it is still difficult to node location estimation accurately and efficiently in WSN since the proposed algorithm should be low complexity and to reduce the communication cost for WSN. It has been shown in the simulation results that the proposed localization scheme can achieve the good localization accuracy in NLOS environments.

Future scope will address the Range map stitching algorithm which is used to provide better localization accuracy in the case of mobile anchor nodes and static blind nodes under the NLOS conditions.

Figures at a glance


Figure 1	Figure 2	Figure 3

Figure 4	Figure 5	Figure 6

References

H. Chen, G. Wang, Z. Wang, H. So, and H. Poor, “Non-line-ofsight node localization based on semi-definite programming in wireless sensor networks,” IEEE Transactions on Wireless Communications, vol. 11, no. 1, pp. 108–116, January 2012.

Oh-Heum Kwon, and Ha-Joo Song, “Localization through map stitching in wireless sensor network,” IEEE Transactions on Parallel and distributed systems, vol. 19, no. 1, January 2008.

SwaroopVenkatesh, and R. Michael Buehrer, “NLOS Mitigation Using Linear Programming in Ultra wide band Location-Aware Networks,” IEEE Transactions vehicular technology, vol. 56, no. 5, September 2007.

Oh-Heum Kwon, Ha-Joo Song and Sangjoon Park, “Anchor-Free Localization through Flip-Error-Resistant Map Stitching in Wireless Sensor Network,” IEEE Transactions on Parallel and distributed systems., vol. 21, no. 11, November 2010.

Stefano Marono, Wesley M. Gifford, and HenkWymeersch, “NLOS Identification and Mitigation for Localization Based on UWB Experimental Data,” IEEE Journal on Selected Areas in Communications, vol. 28, no. 7, September 2010.

HuiSuo, Jiafu Wan, Lian Huang and CaifengZou, “Issues and challenges of wireless sensor network localization in emerging applications,” International Conference on Computer Science and Electronics Engineering, 2012.

Paolo Pivato, Luigi Palopoli, and Dario Petri, “Accuracy of RSSBased Centroid Localization Algorithms in an Indoor Environment,” IEEE Transactions on Instrumentation and Measurement, vol. 60, no. 10, October 2011.

Gang Wang and Kehu Yang, “A New Approach to Sensor Node Localization using RSS Measurements in Wireless Sensor Networks,” IEEE Transactions on Wireless Communications, vol. 10, no. 5, May 2011.