Electrical power industry restricting has created highly vibrant and competitive market that altered many aspects of the power industry. In this changed scenario, scarcity of energy resources, increasing power generation cost, environment concern, ever growing demand of electrical energy necessitate optimal economic dispatch. Practical economic dispatch (ED) problems have nonlinear, non-convex type objective function with intense equality and inequality constraints. The conventional optimization methods are not able to solve such problems as due to local optimum solution convergence. This work proposes a novel metaheuristic optimization methodology aimed at solving economic dispatch problem considering valve point loading effects. The differential evolution (DE) may occasionally stop proceeding toward the global optimum even though the population has not converged to a local optimum. This situation is usually referred to as stagnation. DE also suffers from the problem of premature convergence, where the population converges to some local optima of a multimodal objective function, losing its diversity. Shuffled frog leaping algorithm (SFLA) is a newly developed memetic metaheuristic algorithm for combinatorial optimization, which has simple concept, few parameters, high performance, and easy programming. SFLA and its variants have been successfully applied to various fields of power system optimization. The proposed approach is based on a hybrid shuffled differential evolution (SDE) algorithm which combines the benefits of SFLA and DE.
Keywords |
| Economic Dispatch, Differential Evolution, Shuffled frog leaping algorithm, shuffled differential evolution. |
INTRODUCTION |
| Economic load dispatch (ELD) problem is a classical form of optimization problems and has been one of the most
important decision-making processes in the operation of electrical power systems. The total system-wide generation
cost is generally defined as the objective function of ELD problem. The equality and inequality power system
constraints are embedded in ELD formulation, such as power balance and generation limits of each generating unit’s
output capacity. ELD problem has been thought of as a mathematically complex and highly nonlinear optimization
problem, especially in larger systems. For many decades, many algorithms have been presented to solve the
optimization problem of ELD. First, conventional deterministic approaches which resort to mathematical gradient
information have been developed to obtain the minimum cost of ELD problem. To overcome the limitations of those
deterministic algorithms in real-system applications which are basically associated with the simplification of
mathematical formulation, a variety of evolutionary frameworks that employ metaheuristic computational intelligence
have explored their capabilities to search optimal solution of ELD problem with little abbreviation of original
formulation. |
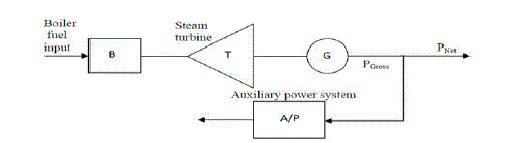
| Steam (Thermal) Units Characteristic The thermal unit system generally consists of the boiler, the steam turbine
and the generator. Fig. showed a typical boiler-turbine-generator unit. The input of the boiler is fuel, and the output is
the volume of steam. |
| The electrical output of this set is connected not only to the electric power system, but also to the auxiliary power
system in the power plant. For thermal units, we call the input-output characteristic the generating unit fuel
consumption function or operating cost function. The unit of the generator fuel consumption function is Btu (British
thermal unit) per hour heat input to the unit (or MBtu/hr or Rs/hr or $/hr). The fuel cost rate times Btu/hr is the $ per
hour ($/hr) input to the unit for fuel. The output of the generating unit will be designated by Pg the megawatt net power
output of the unit. |
SMOOTH OPERATING COST CURVE OF A THERMAL UNIT |
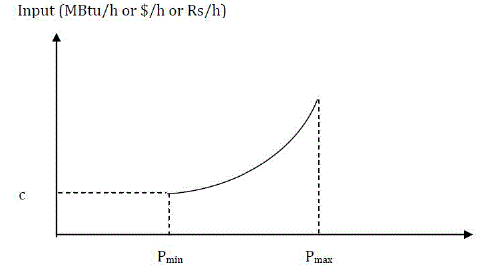
| The input-output characteristic of the whole generating unit system can be obtained by combining directly the inputoutput
characteristic of the boiler and the input-output characteristic of the turbine-generator unit. It is a smooth convex
curve, which is shown in Fig. 2.2. |
| Generally, the input-output characteristic of generating unit is non-linear. In thermal power plants, fuel cost is an
important criterion for economic feasibility. The economic dispatch problem can be formulated by using quadratic or
cubic functions of generated power. The Let FG mean the cost, expressed for example in dollars per hour, of producing
energy in the generator unit i. The total controllable system production cost such an approach will not be workable for
nonlinear functions in practical systems. Therefore will be |
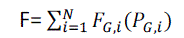 |
| The widely used input-output characteristic of the generating unit is a quadratic function i.e. |
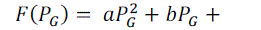 |
| Wherea, b, and c are the cost coefficients of the input-output characteristic. The constant c is equivalent to the fuel
consumption of the generating unit operation without power output, which is shown in Fig.2.2. |
ECONOMIC DISPATCH PROBLEM CONSIDERING VALVE-POINT LOADING EFFECT |
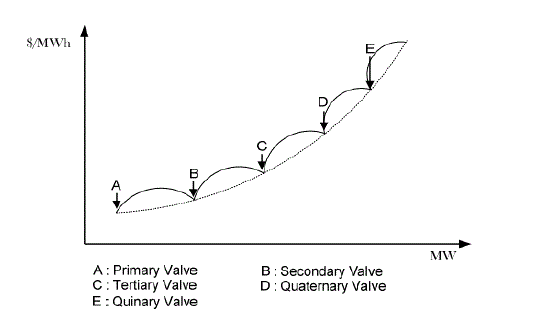
| The generating units with multiple valves in steam turbines are available. The opening and closing of these valves are
helpful to maintain the active power balance. However it adds the ripples in the cost function as shown in Fig. which
makes the objective function highly nonlinear. |
| For more rational and precise modelling of fuel cost function, the above expression of cost function is to be modified
suitably. The generating units with multi-valve steam turbines exhibit a greater variation in the fuel-cost functions [3].
The valve opening process of multi-valve steam turbines produces a ripple-like effect in the heat rate curve of the
generators. These “valve-point effect” are illustrated in Fig. |
| The significance of this effect is that the actual cost curve function of a large steam plant is not continuous but more
important it is non-linear. The valve-point effects are taken into consideration in the ED problem by superimposing the
basic quadratic fuel-cost characteristics with the rectified sinusoidal component as follows: |
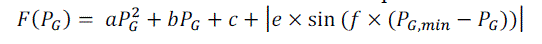 |
| where |
| F is total fuel cost of generation in ($/hr) including valve point loading. |
| e, f are fuel cost coefficients of the generating unit reflecting valve-point effects. |
PROBLEM DESCRIPTION |
| The ELD problem can be stated as to determine the optimal set of individual generating units’ generation outputs
minimizing the objective function(s) as well as satisfying both the equality and inequality constrains. The ELD can,
therefore, be mathematically formulated as a continuous variable optimization problem. The objective function to be
minimized can be defined as the system-wide generation cost across all the generators. Equality constraint of ELD is a
power balancing equation where total power supply of all the generators is equal to the total system demand plus
system loss. In addition, individual generators’ generation output should be in-between its minimum and maximum
generation capacity, and this condition is imposed as the inequality constraint for each generator’s output in ELD
problem. The mathematical formulation of the generic ELD problem can, therefore, be described as follows: |
Minimize 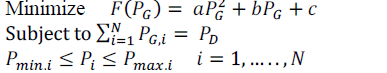 |
| Moreover, more practical consideration of ELD problem requires an inclusion of valve-point loading effects in ELD
problem, and the mathematical formulation of ELD with valve-point loading can be rephrased as follows:
Minimize |
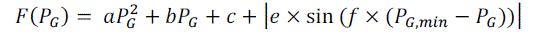 |
SOLUTION METHODS FOR ECONOMIC LOAD DISPATCH |
| A wide variety of technique has been reported to obtain solution Economic dispatch problem. As it is an optimal
problem, broadly optimization techniques are clamped as |
| 1. Conventional method |
| 2. Artificial neural method |
1. Conventional method |
| When making a decision in order to achieve a certain goal, a optimization techniques such as
mathematical programming have been utilized in cases where the largest problem can be expressed as a power
economical dispatch (PED). On the other hand, if the target problem cannot be expressed in a mathematical
equation, neural network, fuzzy logic, expert systems and other decision- making techniques have been utilized.
The problem with conventional technique is the difficulty in guaranteeing the generation of good quality solutions for cases that have not been verified. It has also a slow convergence of optimization procedure. Some conventional
methods are: |
| i. Lagrangian method The method of Lagrange multipliers can also accommodate multiple constraints.To see
how this is done, we need to reexamine the problem in a slightly different manner because the concept of “crossing”
discussed above becomes rapidly unclear when we consider the types of constraints that are created when we have
more than one constraint acting together. |
ii. Gauss seidal method |
| The Gauss–Seidel method, also known as the Liebmann method or the method of displacement, is an iterative
method used to solve a linear system of equations. It is named after the Ger man mathematicians Car l
Friedrich Gauss and Philipp Ludwig von Seidel, and is similar to the Jacobi method. Though it can be applied
to any matrix with non- zero elements on the diagonals, convergence is only guar anteed if the matrix is either
diagonally dominant, or symmetric and positive definite. |
iii. Gradient method |
| The gradient method is an algorithm for the numerical solution of particular systems of linear equations,
namely those whose matrix is symmetric and positive- definite. The conjugate gradient method is an iterative
method, so it can be applied to sparse systems that are too large to be handled by direct methods such as the
cholesky decomposition. Such systems often arise when numerically solving partial differential equations. |
iv. Newton raphson method |
| Newton method is a method for finding successively better approximations to the roots (or zeroes) of a real- valued
function. The idea of the method is as follows: one starts with an initial guess which is reasonably close to the true
root, then the function is approximated by its tangent line (which can be computed using the tools of calculus), and one
computes the x-intercept of this tangent line (which is easily done with elementary algebra). This x-intercept will
typically be a better approximation to the function's root than the original guess, and the method can be iterated. |
1 Artificial neural method |
| Artificial method has an advantage in that a good quality solution can be obtained even in cases when
the target problem cannot be expressed as an equation. Rather than optimization within a small range, as is often said,
end users require “total optimization” over a broad range. In comparing with convergence time, it is able to do it in
lesser time than conventional methods. Some artificial neural methods are: |
i. Genetic Algorithm (GA): |
| A global optimization technique known as genetic algorithm (GA) has emerged as a candidate due to its
flexibility and efficiency for many optimization applications. Genetic algorithm is a stochastic searching algorithm. It
combines an artificial, i.e. the darwinian survival of the fittest, principle with genetic operation, abstracted from
nature to for m a robust mechanism that is very effective at finding |
ii. Evolutionary programming (EP) |
| Evolutionary computing is an adaptive search technique based on the principles of genetics and natural selection.
Evolutionary programming is a probabilistic, global technique. It starts with a population of randomly generated
candidate solutions and evolves towards better solutions over a number of generations or iterations. The main stages of
this technique include initialization, mutation, competition and selection. |
iv. Adaptive neural network (ANN) |
| Adaptive control theory has evolved as a powerful methodology for designing nonlinear feedback
controllers for systems with parametric uncertainty. The fundamental issues of adaptive control for linear systemsselection
of controller structures, assumptions of a priori system knowledge, parameterization of adaptive
systems, establishment of error models, development of adaptive laws, persistency of excitation, and analysis of
closed- loop stability have been extensively addressed. |
DIFFERENTIAL EVOLUTION (DE) |
| Differential evolutionary Programming is a population-based stochastic function minimizes (or maximize)
relating to evolutionary computation, whose simple yet powerful and straightforward features make it very
attractive for numerical optimization. Differential evolution uses a rather greedy and less stochastic approach to
problem solving than do evolutionary algorithms. Differential evolution combines simple arithmetic operators with
the classical operators of recombination, mutation and selection to evolve from a randomly generated starting
population to a final solution. |
Equality Constraints for Active Power Balance |
| The total power generated should be the same as the total load demand plus the total transmission losses. In this work,
transmission power losses have not been considered and the active power balance can be expressed as: |
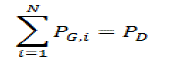 |
| Where, PD is the total power demand in MW. |
Inequality Constraints for Generation Capacity |
| It is not always necessary that all the units of a plant are available to share a load. Some of the units may be taken off
due to scheduled maintenance. Also it is not necessary that the less efficient units are switched off during off peak
hours. There is a certain amount of shut down and start up costs associated with shutting down a unit during the off
peak hours and servicing it back on-line during the peak hours. To complicate the problem further, it may take about
eight hours or more to restore the boiler of a unit and synchronizing the unit with the bus. To meet the sudden change in
the power demand, it may therefore be necessary to keep more units than it necessary to meet the load demand during
that time. This safety margin in generation is called spinning reserve. The optimal load dispatch problem must then
incorporate this startup and shut down cost for without endangering the system security. |
| The power generation limit of each unit is then given by the inequality constraints |
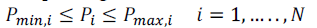 |
| The maximum limit Pmax is the upper limit of power generation capacity of each unit. On the other hand, the lower limit
Pmin pertains to the thermal consideration of operating a boiler in a thermal or nuclear generating station. An operational
unit must produce a minimum amount of power such that the boiler thermal components are stabilized at the minimum
design operating temperature. |
CASE STUDIES AND ANALYSIS |
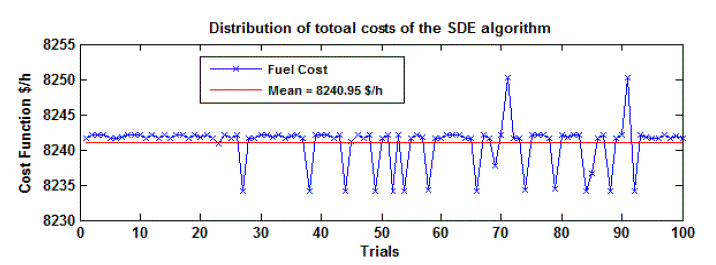
| In the Table 1, SDE method is also compared with the GA [3] and MPSO [12] methods. The minimum cost for GA [3]
and MPSO [12] is 8234.60 $/h and 8234.07 $/h respectively Fig. 5.2 shows the distribution of total costs of the SDE
algorithm for a load demand of 850 MW for 100 different trials for 3-unit case study and observed that the maximum,
minimum and average values are 8250.2047 $/h, 8234.0717 $/h and 8240.9518 $/h respectively. The mean values also
highlighted with red line in the fig. 4. |
Thirteen unit case study system |
| The proposed hybrid algorithm is applied on 13-unit system with the effects of valve-point loading. |
| The problem is solved for two different power demands in order to show the effectiveness of the proposed method in
producing quality solutions. In the first case, the expected load demand to be met by all the thirteen generating units is
1800 MW. The load demand is set at 2520 MW in second case. The data of the test system have been obtained. |
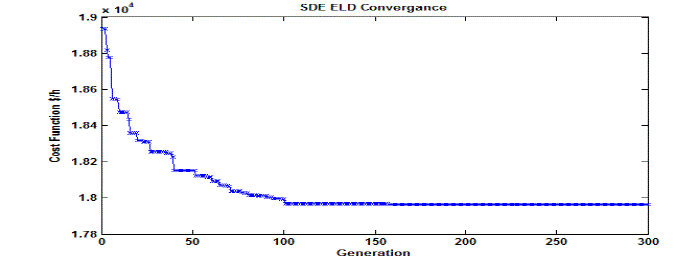
| Table 2 shows the best dispatch solutions obtained by the proposed method for the load demand of 1800 MW. The
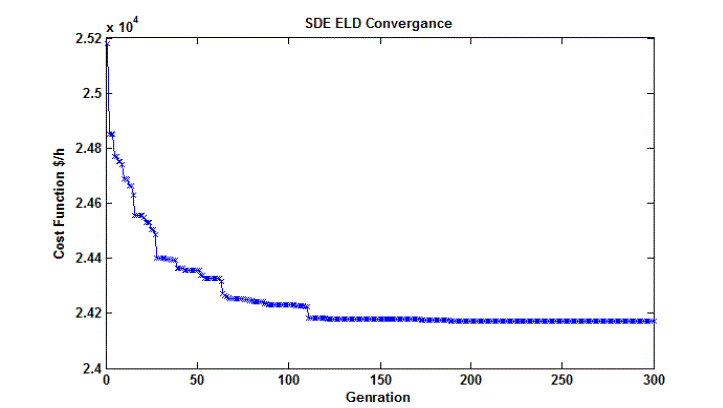
convergence profile for SDE method is presented in Fig. 5. The results obtained by the proposed methods are compared
with those available in the literature as given in Table 5.2. Though the obtained best solution is not guaranteed to be the global solution, the SDE has shown the superiority to the existing methods. The minimum cost obtained by SDE
method is 17963.8293 $/h, which is the best cost found so far and also compared the SDE method with the IGA_MU
[41] and HQPSO [42] methods. The minimum cost for IGA_MU [41] and HQPSO [42] is 17963.9848 $/h and
17963.9571 $/h respectively. The results demonstrate that the proposed algorithm outperforms the other methods in
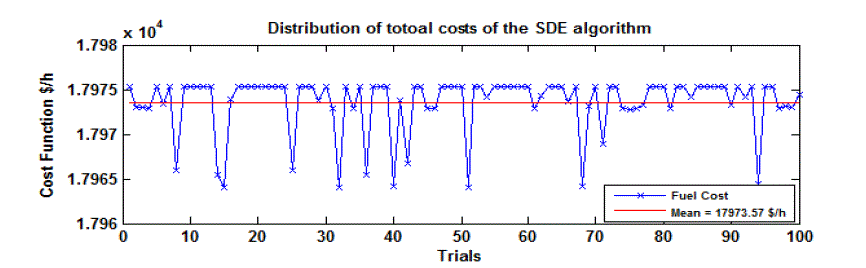
terms of better optimal solution. Fig. 6 shows the variations of the fuel cost obtained by SDE for 100 different runs and
convergence results for the algorithms are presented in Table 5.3 for 1800MW load. |
| Fig. 7 shows the variations of the fuel cost obtained by SDE for 100 different runs and convergence results for the
algorithms are presented in Table 5.3 for 1800MW load. |
| Table 3 shows the convergence results for 100 trials for 13-unit test system with load 1800 MW and compared the
minimum, average and maximum cost for IGA_MU [41] and HQPSO [42] methods. It has been observed that
minimum, average and maximum costs for SDE proposed method is 17963.8293 $/h, 17972.8774 $/h and 17975.3434
$/h respectively and also observed that the proposed method minimum, average and maximum cost values are low
compared with the IGA_MU [41] and HQPSO [42] methods. |
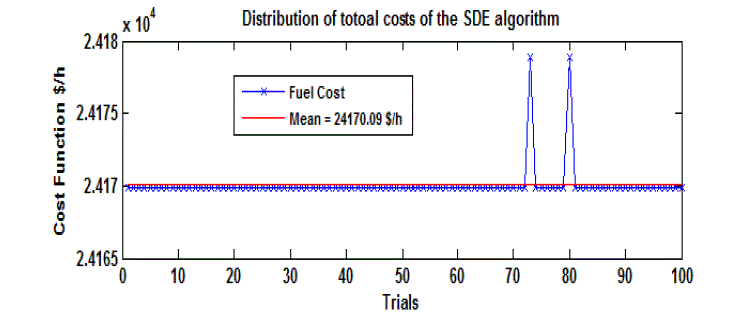
| Table 4 shows the best dispatch solutions obtained by the proposed method for the load demand of 2520 MW. The
convergence profile for SDE method is presented in Fig. 7. The results obtained by the proposed methods are compared
with those available in the literature as given in Table 4. Though the obtained best solution is not guaranteed to be the
global solution, the SDE has shown the superiority to the existing methods. The minimum cost obtained by SDE
method is 24169.9177$/h, which is the best cost found so far and also compared the SDE method with the GA_MU [48]
and FAPSO-NM [20] methods. The minimum cost for GA_MU [48] and FAPSO-NM [20] is 24170.7550 $/h and
24169.92 $/h respectively. |
| The results demonstrate that the proposed algorithm outperforms the other methods in terms of better optimal solution.
Fig. 8 shows the variations of the fuel cost obtained by SDE for 100 different runs and convergence results for the
algorithms are presented in Table 5 for 2520 MW load. |
Forty unit case study system |
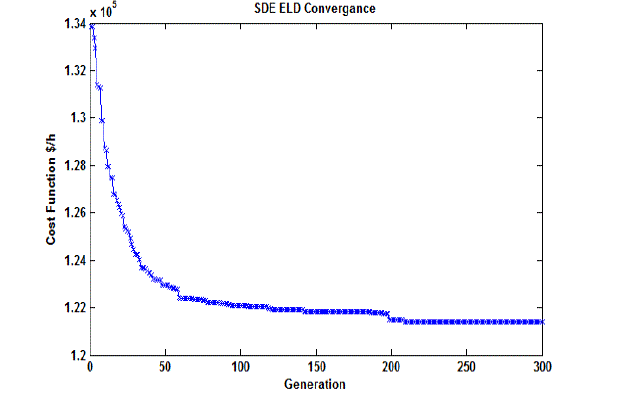
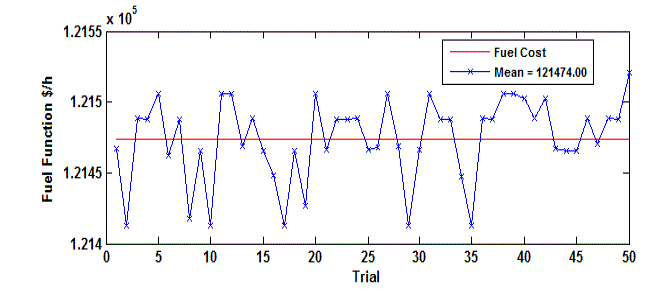
| The ED problem has been solved for a 40 thermal unit’s power system considering the effects of valve-point loading
effects. The load demand is 10500 MW. The system data can be found in [7] and given in Table A3. |
| Table 6 shows the convergence results for 100 trials for 13-unit test system with load 1800 MW and compared the
minimum, average and maximum cost for BBO [16] and ACO methods. It has been observed that minimum, average
and maximum costs for SDE proposed method is 121412.5355$/h, 121474.0032$/h and 121521.0211$/h respectively. |
CONCLUSION |
| Economic Load Dispatch is one of the fundamental issues in power system operation. The problem of economic load
dispatch with equality and inequality constraints has been investigated in this thesis. A novel hybrid heuristic method
has been considered with simple active power balance, generation unit limits and valve point loading and successfully
applied for non-convex economic dispatch problems solution. The proposed approach is based on a hybrid shuffled
differential evolution (SDE) algorithm which combines the benefits of shuffled frog leaping algorithm and differential
evolution. The SDE algorithm integrates a novel differential mutation operator specifically designed for effectively
addressed the problem. In order to validate the proposed methodology, detailed simulation results obtained on three
standard test systems having 3, 13, and 40-units have been presented and discussed. The simulation results showed as
the proposed method succeeded in achieving the goal of reduction generation costs. A comparative analysis with other
settled nature-inspired solution algorithms demonstrated the superior performance of the proposed methodology in
terms of both solution accuracy and convergence performances. Also it has better results compared to the other existing
optimization techniques in terms of generation cost and constraints satisfactions and computation time. Therefore, the
proposed method can greatly enhance the searching ability; ensure quality of average solutions, and also efficiently
manages the system constraints. |
Tables at a glance |
 |
 |
 |
 |
| Table 1 |
Table 2 |
Table 3 |
Table 4 |
|
|
Figures at a glance |
 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
 |
 |
 |
 |
 |
| Figure 6 |
Figure 7 |
Figure 8 |
Figure 9 |
Figure 10 |
|
References |
- Mahor A, Prasad V, Rangnekar S. Economic dispatch using particle swarm optimization: a review. Renew Sust Energy 2009;13(8):2134–41.
- Wood AJ, Wollenberg BF. Power generation operation and control.John Wiley & Sons; 1984.
- Walters DC, Sheble GB. Genetic algorithm solution of economic dispatch with valve point loading. IEEE Trans Power Syst 1993;8(3):1325–32.
- Neto JXV, Bernert DLA, Coelho LS. Improved quantum-inspired evolutionary algorithm with diversity information applied to economic dispatch problem with prohibited operating zones. Energy Convers Manage 2011;52(1):8–14.
- Liang ZX, Glover JD. A zoom feature for a dynamic programming solution to economic dispatch including transmission losses. IEEE Trans Power Syst1992;7(2):544–50.
- Yang HT, Yang PC, Huang CL. Evolutionary programming based economic dispatch for units with nonsmooth fuel cost functions. IEEE Trans Power Syst1996;11(1):112–8.
- Sinha N, Chakrabarti R, Chattopadhyay PK. Evolutionary programming techniques for economic load dispatch. IEEE Trans EvolComput 2003;7(1):83–94.
- Victoire TAA, Jeyakumar AE. Hybrid PSO–SQP for economic dispatch with valve-point effect.Electr Power Syst Res 2004;71(1):51–9.
- Vlachogiannis JG, Lee KY. Economic load dispatch – a comparative study on heuristic optimization techniques with an improved coordinated aggregation basedPSO. IEEE Trans Power Syst 2009;24(2):991–1001.
- Selvakumar AI, Thanushkodi K. Optimization using civilized swarm: solution to economic dispatch with multiple minima. Electr Power Syst Res 2009;79(1):8–16.
- Meng K, Wang HG, Dong ZY, Wong KP. Quantum-inspired particle swarm optimization for valve-point economic load dispatch. IEEE Trans Power Syst2010;25(1):215–22.’
- Park J-B, Lee K-S, Shin J-R, Lee KY. A particle swarm optimisation for economicdispatch with nonsmooth cost function. IEEE Trans Power Syst 2005;20(1):34–42.
|