International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Obstacle-Avoiding Rectilinear Steiner Minimum Tree: A Survey

Arpana Bhagwat1
 PG Student, Department of CSE, BMS College of Engineering, Bangalore, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Rectilinear Steiner Minimum Tree (RSMT) is one of the global routing techniques in VLSI design, where the tree spans a given set of pins by reaching each of them either vertically or horizontally.While constructing such RSMTs, there can be many obstacles.There are many research works done in order to construct RSMTs which aredevoid of obstacles. Some of the recent research works are considered in this paper to understand the problem and to learn the available solutions.It covers and compares different approaches and methodologies which are used to find OARSMT. Some of the different approaches discussed here are Geo-Steiner approach, Maze routing method, Top-down partitioning approach and Greedy heuristic method.Comparison of these algorithms in accordance with their speed, efficiency, resources used and other pros and cons are also listed as a part of this work. A table listing the experimental results ismadeto realize the actual performance of different algorithms.

Keywords
Rectilinear Steiner Minimum Tree, Obstacles, Slew Constraint.

INTRODUCTION
Steiner tree problem can be defined as “Given a set „P‟ of n number of input points, a new set of points S called a set of Steiner points need to be found such that the length of the path spanning the points „P U S‟ is minimum”. In case of Rectilinear Steiner Minimum Tree (RSMT), the edge connecting any two points must be either horizontal or vertical. Obstacles are rectangular blockages over which connecting edges/wires are not allowed most of the times. Obstacles do not overlap on each other but can have common edges or common vertex point. In the original RSMT, it was assumed that there are no obstacles but in real world applications we come across some of the common obstacles like routing blockages, pre-routed nets, IP blocks, macro cells in case of VLSI design.
Now the actual challenge is to have an efficient and fast performing algorithm to get „Obstacle Avoiding Rectilinear Steiner Minimum Tree - OARSMT‟. In case of incremental approach for finding OARSMT, initially OARSMT is generated considering empty list of obstacles and then the obstacles are introduced in the obstacle listleading to a refining of previously generatedOARSMT. Iterationsare carried out until obstacle overlapping is found during this process. Sometimes a slight variation in the problem statement is found, in which it says the not all the edges have to be avoided over an obstacle but to have a constraint so that the maximum length of edge/s should not cross some threshold called slew constraint.This is taken from the fact that wires are allowed over the blockages but not buffers or repeaters which in turn limits the length of the wire allowed over an obstacle.
At global routing phase of VLSI designOARSMT is used, this makes an ideal use case as at this stage of VLSI design there exist some macro cells which are built for performing specific functionalities in a chip and are characterized by their rectangular shape. There are somemoreapplications of RSMT in VLSI design itself. Computer system networking is one more area of its application where the computers are interconnected with multiple cables and wires; RSMT is used for finding the minimum wire length. In case of communication networks, RSMT is useful for multicast routing.RSMT is used for spanning all the nodes which are part of multicasting and identifying a shortest path for the communication.
Upcoming sections will include the survey, comparison of their experimental results and finally the conclusion.

SURVEY: APPROACHES TO OA-RSMT
This section includes the survey of different papers which are written on the concept of OARSMT. This survey includes a brief note on the methodology and algorithm which is explained in the implementation papers.

 GeoSteiner Approach [1]
Full Steiner Trees (FSTs) are the building blocks of a GeoSteiner approach. In an FST, all the pins in consideration are leaf nodes. GeoSteiner framework includes mainly 2 phases. First one is being the FST generation, which includes pruning away of unnecessary nodes based on some preprocessing information. It is observed that the runtime of this phase is quadratic. Secondphase is the concatenation of FSTs which are generated at phase one. It can be foreseen as an Integer Linear Program (ILP) and can be solved using branch and cutsearch method. Initially a set of actual pins are taken into consideration. Each corner of every obstacle is considered as a virtual pin. For FST generation these virtual pins are also included without being bothered whether these are considered in the final optimal tree generation. In the incremental method of FST generation FST is first generated for two points which can be done in any of the two ways,first is both the points are real points and second isat least one of the points is virtual. Techniques are adopted to make sure the redundant edges which are created due to multiple FSTs are removed. The same method is extended to recursively generate three and more point FSTs. Once all the useful FSTs are generated, ILP is set up in order to select appropriate subset of FSTs and concatenate them to get an OARSMT.

 An Optimal Approach[2]
This is the work done as an enhancement on [1]. The paper proposing this method says that OAFSTs are generated and used instead of using FSTs. A two phase algorithm is proposed; of which first phase is OAFST generation and second phase is OARSMT construction using OAFSTs. In this method only two virtual points are used for each obstacle and incremental method of handling obstacles is used to get a reduced run time. OAFSTs for every terminal are generated recursively by using bottleneck Steiner distance, empty diamond, empty corner rectangle and empty inner rectangle properties.At second phase these OAFSTs are used to generate OARSMTs by formulating it to ILP and using branch and cut search to solve it. This method incorporates incremental method so that it can avoid OAFST explosion.

 Slew Constraints over Obstacles[3]
This conceptcontains analysis of an optimal solution for finding OARSMT with slew constraints and then a proposal of an algorithm to find optimal solution embedded in the extended Hanan Grid.Given a source and a set of sink points, RSMT is generated and called as T. A new type of points is considered called as a set of boundary terminals. These are the nodes which lie on obstacles boundaries and all of them have at least one of the incident lines passing through the obstacle. The tree T is decomposed into smaller trees till we have a clear partition as the ones which are lying completely inside the obstacle (Ti) and the others which are completely outside the obstacle (To). An assumption is made that the buffers can be inserted only to „To‟ but not to „Ti‟ except that which can be inserted at the boundary terminals. Hence in order to maintain the signal quality in „Ti‟slew constraints are introduced. In this paper slew rate is considered to be the time taken for a waveform to cross the 10% point and the 90% form.The algorithm proposed contains two phases. In first phase the candidate trees for „Ti‟ and „To‟ are generated and in the second phase a subset of these threes is identified and the trees are combined to give an optimal solution. Along with the experimental results this paper claims to have 800 times speedup and about 5% reduction in routing resources in reference with state-of-the-art optimal OARSMTalgorithm.

 High-Performance Solution[4]
A new routing graph called Obstacle Avoidance Routing Graph (OARG) is proposed in this work and a three step algorithm with refinement scheme to find a sub-optimal solution for an OARSMT problem is given.The three step algorithm can be summarized as the first step is to construct OARG with O(n log n) time complexity and O(n) as space complexity, second step is of MST-OARG construction in O(n log n) time and the third step is for OARST transformation from MST-OARG using a scheme called as MST-OARG reduction. During local refinement process total wire length reduction is done for OARST. General cases are used in this refinement schemeand sorting method is used to make the scheme greedier. Wire length estimated by the three step algorithm can be reduced significantly in O(n log n) time. As mentioned OARG in this work maintains O(n) space hence contributing in the better initial solution to O(nlog n) time. Also it significantly contributes to the performance with its linear space and obstacle avoidance properties.

 Based On Steiner Point Selection[5]
This work proposes an algorithm based on Steiner point, to achieve performance speedup and reduction in wire length. It claims to achieve this solution in Θ(n log n)empirical time which otherwise takes Ω (n2) time using maze routing in Space Graph.The usage of Steiner point based framework can be even extended to multilayer OARSMT and OA preferred direction RSMT. The algorithm is divided into four steps. Graph construction, Steiner point selection, minimum terminal spanning tree (MTST) construction and finally refinement. MTST is the tree where the tree spans only the given set of terminals without spanning any other intermediate vertices. Hanan Grid and escape graphs are used to find the Steiner point location. Both of these generate a vertex at the intersection of the extended lines from terminals or obstacle corners. However this creates a large number of such vertices which makes the vertex selection take longer time. Hence this algorithm follows a different approach.In graph construction step Obstacle Avoiding Voronoi Graph (OAVG) is constructed with a given set of terminals, obstacle vertices and desirable Steiner point candidates in O(n log n) time. Good Steiner points are then selected from the constructed OAVG using Prim‟s algorithm and Shortest Path Region (SPR) bounded by the two terminals. In the third step OARST is constructed in O(n log n) time using MTST algorithm proposed by Long and Liu. MTST on OAVG is constructed spanning the given vertices and the selected Steiner points. Long‟s MTST algorithm includes the terminal path generation and also MST generation using these paths and Liu‟s algorithm has directly critical path generation. Refinement is done in O(n log n) time to reduce redundant segments created in the above steps.

 Critical-Trunk Based Approach for Delay and Slack Optimization[6]
Critical trucks are constructed by extending the single source single target maze routing on all the sources which is even called as multi source single target maze routing, later connecting the unconnected points at the delay constraint of every sink. This paper has a glance of previously proposed algorithms by different researchers and it shows that sometimes efficiency can be a tradeoff with performance. Critical trunk based tree growth algorithm is used to solve two main problems. First is Performance Driven OARST (PDOARST) and second one is Slack Driven OARST (SDOARST). The goal of PDOARST is to have the minimum delay at each sink. Sometimes reducing the maximum delay might create problems with respect to timing constraints. SDOARST is given to satisfythe timing constraints and to solve Worst Negative Slack (WNS) violations. Two algorithms are proposed, one for each of the above problems, both are having four steps and which are similar at step level. It starts with OASG construction following PD/SD critical trunk growthand then the PD/SD sub tree growth. PDOARST ends after making the tree rectilinear and applying refinement on it. Final two steps of SDOARST contain rectilinearization and redirection to maximize the WNS of the OARST.

 FOARS[7]
FOARS (FLUTE Based Obstacle-Avoiding Rectilinear Steiner Tree Construction) follows a top-down divide and conquer approach. Initial solution is partitioned into multiple sub problems using Obstacle Aware Fast LookUp Table based wirelength Estimation (OA_FLUTE) in order to generate OARSTs and then recombine them. To make the initial connected graph, FOARS uses OASG.FLUTE is a very robust and speed tool get the RSMT and is widely used in academic global routers but FLUTE is not built for handling obstacles. To create OARSMT the SRT generated using FLUTE is applied with obstacles, local optimization is done and later all the locally optimized trees are combined to get the final solution. But since there is no global view taken into consideration, this scheme fails to support large number of points or complexly placed obstacles. To overcome this issue partitioning algorithm is proposed which provides a global view for the problem at higher level and partition problem into smaller ones. This algorithm is divided into five stages. OASG generation-connectivity graph is generated novel octant OASG generation algorithm. Obstacle Penalized MST (OPMST) generation- MTST is generated from OASG and OPMST is generated from MTST.OAST generation- Based on OPMST, partitioning is done and the partitioned are processed under OA_FLUTE.OARST generation – Rectilinearization is done and later V-shape refinement is done to reduce the wire length.Run time complexity of FOARS algorithm is O(n log n).

 Buffering-Aware Rectilinear Steiner Minimum Tree Construction[8]
An algorithm is proposed to Buffering-aware Over the Block RSMT (BOB-RSMT) as a part of this work. It helps in reducing the routing resources under the limit of slew constraints as compared to OARSMT. This is an incremental algorithm where initially an RSMT is constructed using FLUTE. For the part of the RSMT which is falling inside the obstacles, slew constraints are checked and the edges are modified accordingly.There are some important points to be noticed with regards to this algorithm. It initially consists of generation of Steiner points on the obstacle boundaries so that the slew is kept to a minimum value. Next is to refine this point set so the tradeoff between the wire length and the slew value is balanced and then to formulate it into ILP. Once the points are fixed,maze routing is applied to get an over-the-blockage tree. At last the slew mode buffers are inserted into the tree at any unblocked location.

 Length Restrictions on Obstacles[9]
This work presents 2-approximation algorithm to solve OARSMT problem with the worst case time complexity of O(n log n)2. This algorithm consists of two phases, at the beginning a visibility graph is constructed to span all the given terminals and the corner points of obstacles. Dijkstra-Kruskal approach is used to construct the Steiner tree for these points. Simple local search heuristics are used as a post-optimization step.

 Timing-Driven, Pre-Buffering and Slew Constraints[10]
Contributions of this work are that it tries to reduce the delay to critical sinks and reduces the wire length to other sinks by using over-the-block routing, it satisfies the slew constraints and which places the buffers in nonblocked places, pre-buffering is used to provide a timestamp leading to be useful in finding good topology with respect to time and optimization is done on the constructed tree to improve the delay to critical sinks.The approach proposed in this paper is time-driven, over-the-block RST with slew constraints. It consists of mainly five steps. First is the construction of timing-driven initial RST „T‟with pre-buffering. Then change the topology of T to in accordance with the slew constraints. Later perform buffering on T. Refine the topology of T based on buffering information. Again perform buffering on T.

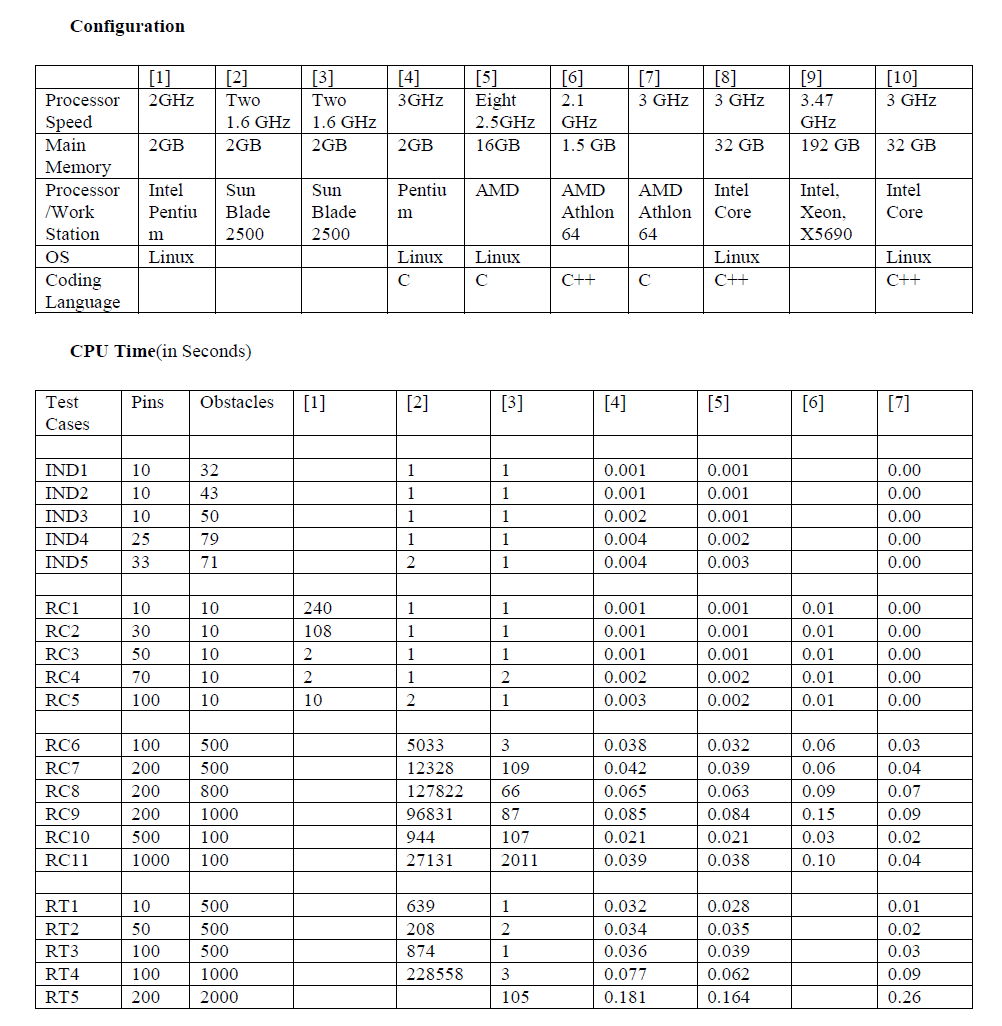
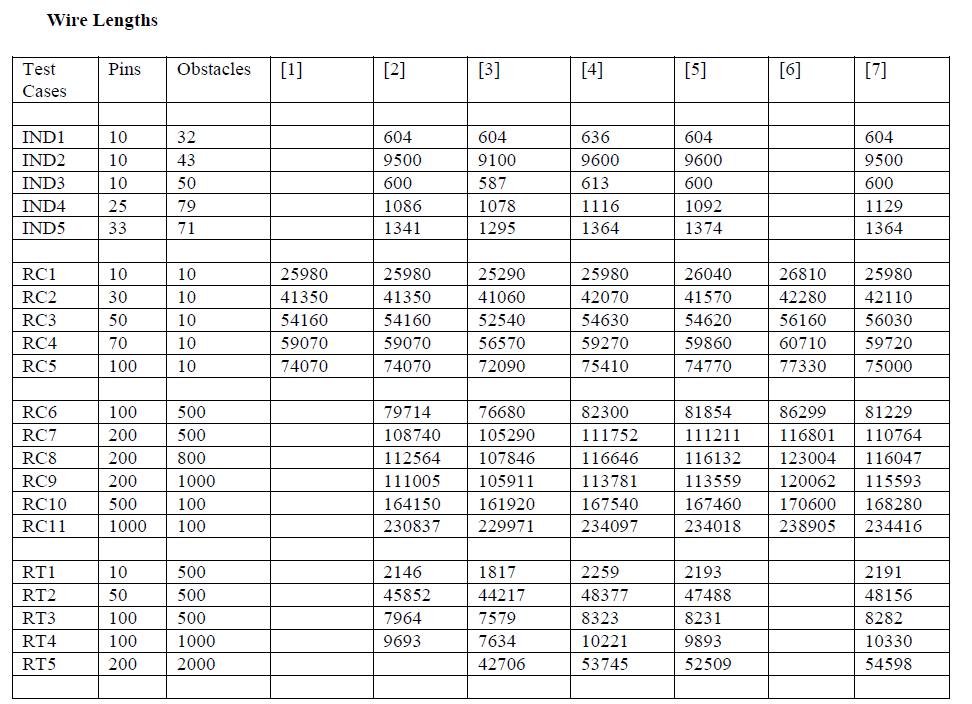
CONSOLIDATED EXPERIMENTAL RESULTS
This section contains the configuration of the system for the algorithms as denoted by the reference numbers. Execution time and wire length for different benchmarks are also listed in this section for respective algorithms. For a few algorithms the same are not added because their results depend on some more parameters like slew constraints.
image
image

CONCLUSION
This paper makes an attempt to give a brief idea about OARSMT and some recent approaches to solve this problem. This work even tries to compare them as per their experimental results and the other parameters as claimed in the respective reference papers. Future work would include a step towards verifying the listed algorithms by implementing them on a common platform.

ACKNOWLEDGEMENT
The authors would like to acknowledge and thank Technical Education Quality Improvement Program [TEQIPII], BMS College of Engineering and SPFU [State Project Facilitation Unit], Karnataka for supporting the work reported in this paper.

References
  1. Liang Li, Zaichen Qian, Evangeline F. Y. Young,“Generation of Optimal Obstacle-avoiding Rectilinear Steiner Minimum Tree”,Computer-Aided Design - Digest of Technical Papers, IEEE/ACM International Conference on 2-5Nov. 2009
  2. Tao Huang, Evangeline F. Y. Young,“Obstacle-avoiding Rectilinear Steiner Minimum Tree Construction: An Optimal Approach”,IEEE/ACM International Conference on 7-11 Nov. 2010
  3. Tao Huang, Evangeline F. Y. Young,“Construction of Rectilinear Steiner Minimum Trees with Slew Constraints over Obstacles”,IEEE/ACM International Conference on 5-8 Nov. 2012
  4. Chih-Hung Liu, Shih-Yi Yuan, Sy-Yen Kuo, Szu-Chi Wang,“High-Performance Obstacle-Avoiding Rectilinear Steiner Tree Construction”,ACM Transactions on Design Automation of Electronic Systems, Vol. 14, No. 3, Article 45, Pub. date: May 2009
  5. Chih-Hung Liu, Shih-Yi Yuan, Sy-Yen Kuo, and Jung-Hung Weng, “Obstacle-Avoiding Rectilinear Steiner TreeConstruction Based On Steiner Point Selection”,ICCAD‟09 San Jose, California, USA November 2–5, 2009
  6. Yen-Hung Lin, Shu-Hsin Chang, Yih-Lang Li,“Critical-Trunk Based Obstacle-Avoiding Rectilinear Steiner TreeRoutings for Delay and Slack Optimization”,Computer-Aided Design of Integrated Circuits and Systems, IEEE Transactions on (Volume:30 , Issue: 9 )
  7. Gaurav Ajwani, Chris Chu, Wai-Kei Mak,“FOARS: FLUTE Based Obstacle-Avoiding Rectilinear Steiner Tree Construction”,Computer-Aided Design of Integrated Circuits and Systems, IEEE Transactions on (Volume:30 ,Issue: 2 )
  8. Yilin Zhang, Ashutosh Chakraborty, Salim Chowdhury, David Z. Pan,“Reclaiming Over-the-IP-Block Routing Resources With Buffering-Aware Rectilinear Steiner Minimum Tree Construction”,Computer-Aided Design(ICCAD), 2012 IEEE/ACM International Conference on 5-8 Nov. 2012
  9. Stephan Held, Sophie Theresa Spirkl,“A Fast Algorithm for Rectilinear Steiner Trees with Length Restrictions on Obstacles”, ISPD‟14, Petaluma, CA, USA, March 30–April 2, 2014
  10. Yilin Zhang, David Z. Pan,“Timing-Driven, Over-the-Block Rectilinear Steiner Tree Construction with Pre-Buffering and Slew Constraints”,ISPD‟14, Petaluma, CA, USA, March 30–April 2, 2014