ISSN: 2319-9873
ISSN: 2319-9873
Biya Motto Frederic*
Department of Physics, Faculty of Sciences, University of Yaoundé I, P O Box 812, Cameroon
Received: 16 October 2014 Accepted: 28 February 2015 Published: 21 March 2015
Visit for more related articles at Research & Reviews: Journal of Engineering and Technology
Optimal estimator synthesis algorithm for dynamic ship system control is considered. Estimator is constructed in the form of Kalman gain as steady-state Kalman filter. Estimator design is realised by MATLAB codes using account of wind gust noise with a set spectral intensity
Control, Optimal estimator, Kalman filter, Ship dynamic object, gust noise.
In no small way, the great technological progress in automatic control and communication systems during the past years has depended on advances and refinements in the mathematical study of such systems. Conversely, the growth of technology brought forth many new problems to challenge the ingenuity and competence of research workers concerned with theoretical questions.
Obtaining good quality information on vector of state variables for dynamic system is very important when studying the evolution process and synthesis of control functions that insure oriented behaviour in time and space. However, phase coordinate vector is often difficult to get for measurement because of various reasons. In such a case, we can evaluate the coordinate vector through the output vector. Since measurements are done with errors and also considering noise at input of the system, we need indicators based on procedures of stochastic filtering.
In systems with optimal control, we need full information for state vector since in this case the synthesis of regulator is simplified. In case of insufficient measurements, we should solve the problem of determining state vector from observation results through output expressions. When measurements and noise errors are significantly acting on the system, together with the observer, we need to synthesise a special filter while presenting the process either in continuous or discrete time. We consider the solution in continuous time.
Let us assume that the object is described by the matrix equations:
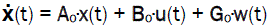 (1)
(1)
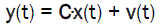 (2)
(2)
Where;
x(t) is (nx1) state vector
u(t) is (mx1) control vector
y(t) is (px1) output vector
Ao, Bo, Go, C are Matrices of corresponding dimensions.
w(t) is the unknown noise acting on the object (such noise can be the influence of the wind or agitation of water surface, etc.)
v(t) is the measurement noise (for example, it can be noise from amplifier)
x(t) Rn, u(t) Rm, y(t) Rp
In case there is no information about the precise value of x(0), then we can use the mathematical expectation ̅(0) and the co-variation matrix Po, then
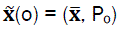 (3)
(3)
Let us consider x(o), w(t) and v(t) as being orthogonal to each other. Much more, suppose that w(t) and v(t) are white noise,
Therefore,
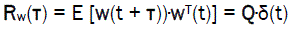 (4)
(4)
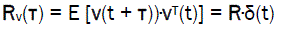 (5)
(5)
Where,
Q and R are matrices of spectral densities,
δ(t) is delta function of Dirac.
Assume that matrices Q and R are known and that R is not a singular matrix, that is
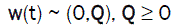 (6)
(6)
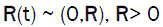 (7)
(7)
We should calculate the observer for stochastic system at entrance of which two signals are acting:
Control signal and output signal from object
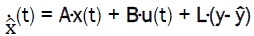 (8)
(8)
or
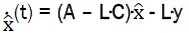 (9)
(9)
Vector 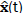 is state evaluator.
is state evaluator.
Output evaluator y is obtained by formula
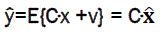 (10)
(10)
Suppose that the couple(C, A) is observable and (A, G√ ) is feasible. Therefore matrix algebraic Riccati equation is the unique positive determined solution of P:
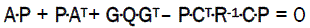 (11)
(11)
Thus, we can synthesize the evaluator L which can assure the best evaluation of error in the presence of noises w(t) and v(t).
If error of the system 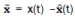 hen we can define it as a solution of matrix differential equation;
hen we can define it as a solution of matrix differential equation;
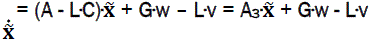 (12)
(12)
Where we use the matrix of constant coefficients of amplification (Matrix of Kalman)
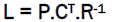 (13)
(13)
The Solution of equation eq12 is stable.
The evaluator eq13 can be called static filter of kalman. It minimizes the error value (co-variation of error) at the completion of transient processes.
The static filter of kalman is the best evaluator that contains constant coefficients. Dynamic equations of the system can contain a model used for transforming white noise into a signal with a given spectral density.
Let us study this point;
Energy spectrum for most of the processes can be represented in the form of square module for a certain function H(jw):
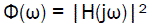 (14)
(14)
It is assumed that a random process with energy spectrum Φ (ω) can be composed of white noise with an energy spectrum equal to that in the frequency diapason -∞ ≤ w ≤ ∞ if it passes though linear filter with frequency characteristic H(jω):
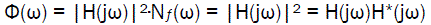 (15)
(15)
Where H*(jω) – conjugate frequency characteristic.
The energy spectrum Φ(ω) can be approximated by rational frequency function, that is a ratio of polynomial function of ω.
Since the energy spectrum is real, even number and not a negative function of ω, then such polynomial should have real coefficients and have only even number degrees of ω:
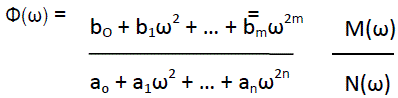 (16)
(16)
From the condition of real coefficients in eq16, poles of energy spectrum can be either real numbers or in pairs of complex conjugates (symmetrical relatively to the real axis).
Impulse and frequency characteristics of the filter are related by the Fourrier transformation. If all the poles of frequency characteristics are lying on the left hand plan then the impulse function is feasible. In that case, the filter happens to be physically realizable. From the complex transfer coefficient, we can establish the transfer function and then synthesize dynamic of obtaining H(s).The canonic form of the system can be defined from the well-known procedure equation [1].
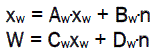 (17)
(17)
Where n(t) is white noise, and w(t) is output random signal with given properties.
Equations eq1, eq2 and eq17 are used for the obtention of enlarged dynamic systems with the following structure:
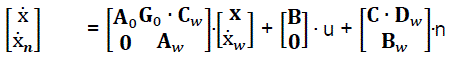 (18)
(18)
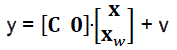 (19)
(19)
We should observe that on input of enlarged system, apart from the control signal u(t) we also have the action from the measurements of noise w(t) and white noise n(t).
Using obtained relations, we will calculate the evaluator – Kalman filter for ship object under the influence of turbulent air flux.
Due to the development and utilization of offshore petroleum resources, the continuous development of marine transport and marine science and technology, ship and ocean engineering technology started rising rapidly. Ship and platform often need to locate their particular position in a site but the traditional way to do so by the anchor method is restricted by the following factors: operating water depth, working time and accuracy demands.
To solve this problem of ship position and maintaining its course, a ship control technology called the dynamic positioning [4,6] at a particular time in history is bringing considerable progress to the development of correlated techniques using the electronic computer, sensors and the control theory.
Dynamic properties of the object are described by equations eq1 and eq2 with the following matrices [2,3]:
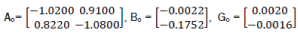
On the object is acting noise with spectral density
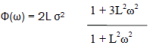
Where σ =10; L = 3.49
Matrix C in equation eq2 has the following coefficients values:
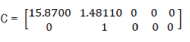
For Kalman filter calculation, assuring minimal errors with noise actions and in Riccati equation eq11 we chose weight matrices Q and R:
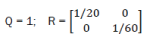
Factorizing of Φ(ω) in the form
Φ(ω) = H(jω)∙H(-jω) enables us to obtain the realizable part of the filter:
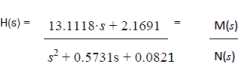
Transformation of H(s) into canonic form of model in states space will be done by function tf2sss, contained in Matlab pack. We then obtained model eq17:
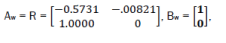
Cw =[13.1118 2.169],Dw = 0
Matrices of enlarged system look as follows.
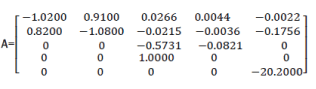
B=[0 0 0 0 20.2]; G=[ 0 0 1 0 0 ]

Kalman transform coefficient is calculated by the aid of Ɩqe function:
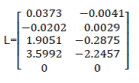
Kalman filter represents dynamic system:
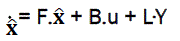 (20)
(20)
Where, the 5th state (the last line of matrix L) is equal to zero because noise does not act directly on the drive of the rudder.
The calculation of filter is done with a program, represented by File sah175a.m, whose content is precised in the text by commentaries.
% File Sah175a.m
% Calculation of stationary Kalman filter.
% Dynamic of the system:
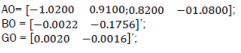
% Determination of the model in state space through
% function of spectral density of external noise signal
sig = 10; L = 3.49;
v = Sig*( (6/L)^0.5);
% Numerator and denominator of complex transform coefficient:
num[1 1/(L*(3^0.5))].*v;
den = [1 2/L 1/(L^2)];
% Determination of states space model with % white noise influence:
[Aw, Bw, Cw, Dw] = tƒ2ss (num, den);
% Formation of generalized dynamic system:
A = [A0 G0*Cw B0;[0 0;0 0;0 0] [Aw;[0 0]] [0 0 -20.2]’];
B = [0 0 0 0 20.2]’;
G = [0 0 1 0 0]’;
C = [15.8788 1.4811 0 0 0; 0 1 0 0 0];
R = [1/20 0; 0 1/60];
Q = [1];
% The filter is synthesis with “ℓqe∙m”.
% The matrix of Kalman amplifier coefficients:
L = ℓqe (A, G, C, Q, R)
Pause,
% Kalman filter: dx/dt = F*x + B*u + L*y;
F = A – L*C
Pause,
% Proper values of the optimal evaluator matrix: eig(F)
The program is ended by calculation of values of matrix F, represented in the form of vector elements:
eig(F) = [-1.1661 -0.3759 -1.5224 -1.1734 -20.2000]T
Finally, through expressions eq17 – eq20 in a Matlab environment, we synthesized the Kalman filter while assuring stability of dynamic process.