This paper deals with the Optimal location and control of a unified power flow controller (UPFC) along with transformer taps are tuned to simultaneously optimize the voltage stability limit (VSL) and real power losses of a radial power system network. This problem is deals with a nonlinear equality and inequality constrained optimization problem with an objective function incorporating both the real power loss and VSL. An Meta-Heauristic algorithm known as Modified shuffled frog leap is applied for solving the UPFC location, its injected voltages are in series, a tap positions of secondary side transformers as they are variables. The obtained results of MSFL Algorithm Compared with Bacteria foregoing algorithm using IEEE 39 bus.
Keywords |
| Modified Shuffled frog leap, continuation power flow (CPF), optimal power flow (OPF).UPFC. |
INTRODUCTION |
| The OPF methods are conventional and intelligent and solved by varieties of methods such as successive linear
programming, the Newton raphson-based nonlinear programming method, and with varieties of recently proposed
interior point methods. The Opf solution is used to optimize a selected objective function such as fuel cost with
optimal adjustment of the power system control variables, at the same time satisfying various equity and inequality
constraints. The drawback of the Optimal power flow is solved from different analysis, like the effects of load on
voltage stability/power flow solvability, generation rescheduling for cost minimization of power generation, controls
such as tap control on transformers, shunt devices, and other modern Var sources adjustments to minimize real power
losses in the system. The advent of Flexible ac transmission systems (FACTS) system made the possibility for
optimizing the power flow without the restoration of generation rescheduling or changes to topology. Unified power
flow controller (UPFC) is the advanced in the controller’s family and can provide the OPF with significant flexibility by
injecting compensation in series and shunt in controlled manner. The UPFC can provide simultaneous control of all
basic power system parameters like (transmission voltages, impedance value and different phase angles). |
| In this paper, the voltage stability limit is defined as the maximum percentage overloading (λmax) the system can
withstand and incorporated along with the objective of real power loss minimization. The classical techniques of OPF
solution has the disadvantage that they are sensitive to starting points and leading monotonic solution. the problem has to
eliminate by using evolutionary techniques has been applied for solving the OPF problem [10], [11] like particle swarm
optimization (PSO) to the problem of OPF. In this paper a new evolutionary algorithm known as Shuffled Frog Leap
algorithm (SFLA) is used to solve the combined problem of CPF-OPF for real power loss minimization and VSL
maximization of the system. The algorithm has been inspired from memetic evolution of a group of frogs when looking
for food. In Sfla, a solution to a given problem is presented in the form of a string, called “frog” which has been
considered as a control vector in this paper. The objective is transformer taps settings , location of UPFC and its
series injected voltage for the single objective of real power loss minimization and then for the multiple objectives
of loss minimization and VSL maximization. Finally, a cost analysis for installation of UPFC is carried out to establish
the investment in putting a UPFC And the Test data results indicate that MSFLA method can obtains the better results
than the simple heuristic search method on the 39-bus radial distribution systems. The UPFC location, series injection
voltage, and Transformer tap positions are simultaneously optimized as control variables, so that the multiple objectives
are fulfilled, keeping an eye to all specified constraints. The results so obtained show its strength in solving highly nonlinear epistatic problems. The main objectives of this paper are to optimize the transformer taps, UPFC location, and
its injection voltage for a single objective of real power loss minimization and then for the multiple objectives of loss
minimization and VSL maximization. For both the cases of single and multiple objectives, are shown in below. |
| 1) Only transformer tap positions are optimized. |
| 2) Keeping the optimized transformer tap positions from the above step fixed, the UPFC variables are optimized. |
| 3) Both the transformer taps and UPFC variables are optimized simultaneously. Finally, a cost analysis for installation of
UPFC is Carried out to establish the investment in putting a UPFC for the cause |
STATEMENT OF THE PROBLEM |
| Problem: To solve a voltage secure real power loss minimization of the ten-machine New England power systems
[15], connected with UPFC by using SLFA and BFA. Both the sequential and simultaneous allocation of transformer
taps and UPFC are carried out for comparison, |
A. Test System: |
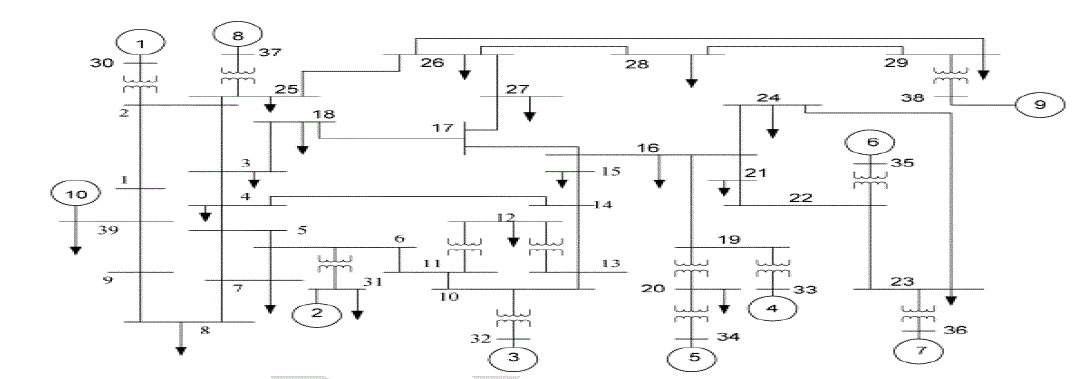
| In this paper, the ten-machine, 39-bus power system shown in Fig. 1 is considered for study. The system details,
including the 12 transformers nominal tap values, are given in [15]. |
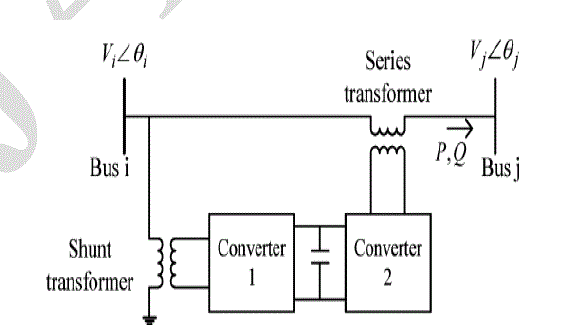
B. Operating Principle of the UPFC and Its Model: |
| The UPFC is a unique device in the family of FACTs devices. It consists of a series and shunt connected converters as
depicted in Fig. 2. |
| It can simultaneously control the real and reactive powers of the line and voltage of the bus at which it is
connected, by injecting proper magnitude of voltage in series and shunt, respectively. In this paper, one UPFC,
with injection model [6], is connected in the system at the suitable location. The UPFC injection model is
presented in Fig. 3. |
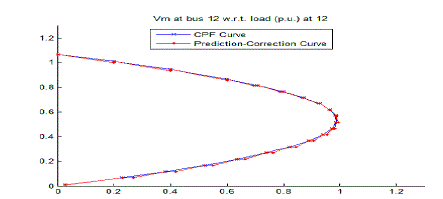
C. continuation power flow: |
| The Jacobin matrix of power flow equations becomes singular at the voltages stability limit. Cpl can
overcomes this problem. It finds out successive load flow solutions according to a load scenario. cpl consists of
prediction and correction steps. From a base solution, a tangent predictor is used so as to Analyse next solution for a
specified pattern of load increase. The corrector step then determines the perfect solution using N-R technique
employed by a cpl. After that a new prediction is made for a specified increase in load based upon the new tangent
vector. |
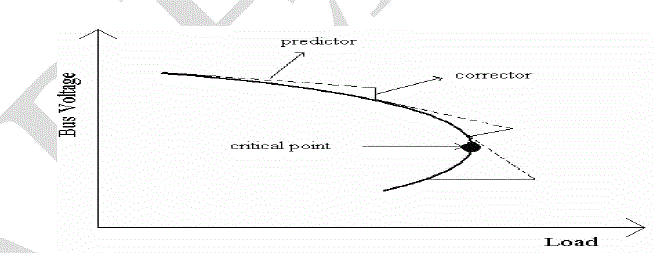
| The continuation power flow methods are powerful and very useful tools for getting solution curves for
general non-linear algebraic equation by automatically changing the value of a parameter. This solution curve indicates
the critical point of voltage stability limit, which is at the nose of the curve. One of the popular CPF techniques is the
one developed by Ajjarapu. This paper presents the development of modified continuation power flow (MCPF) to solve
the failure in convergence experienced in the conventional power flow. The modified CPF technique was based on the
technique proposed by Ajjarapu. The developed technique has also identified the nose point of Q-V curve, which was
discovered to be the failure in the conventional power flow. |
D. Optimal power flow problem |
| It is also important that the proper problem definition with clearly stated objectives be given at the onset. The
quality of the solution depends on the accuracy of the model studied. Objectives must be modeled and its practicality
with possible solutions. Objective function takes various forms such as fuel cost, network transmission losses and
reactive power source allocation. Usually the objective function of interest is the minimization of total production cost
of scheduled generating units. This is most used as it reflects current economic dispatch practice and importantly cost
related aspect is always ranked high among operational requirements in Power Systems. The solution of CPF is carried
out with the help of a suitably chosen continuation parameter. With the increase of “λ” a new solution point is predicted
first and then corrected in usual predictor and corrector steps. Since the objective is to maximize the Voltage stability limit, and its reciprocal is adding to the original exact cost function of real power loss so that the overall cost can be
minimized.. |
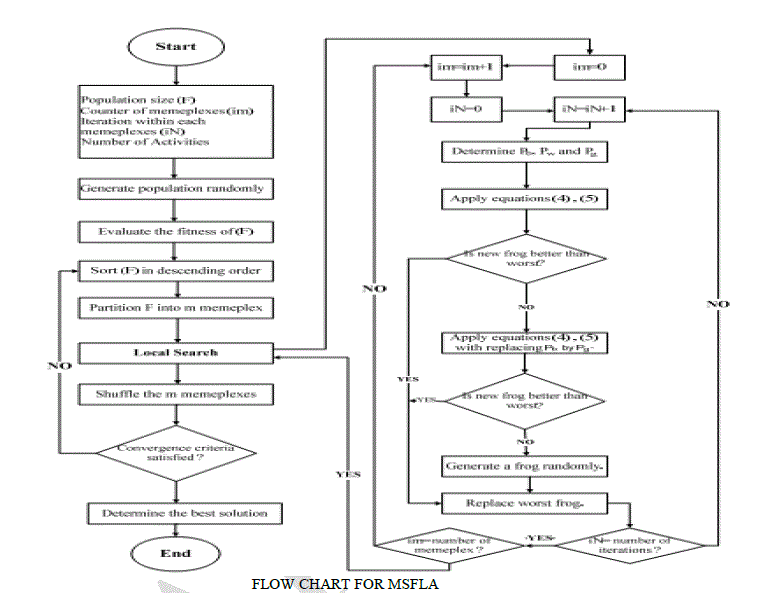
SHUFFLED FROG LEAP ALGORITHM |
| Shuffled Frog Leaping Algorithm is a kind of evolutionary computation method based on swarm intelligence. Eusuff
and Lansey proposed the algorithm in 2001, which is inspired by the frog prey behavior. Shuffled Frog Leaping
Algorithm is similar to Memetic Algorithm, which is based on group cooperative search .At the same time, it is also
provided with the advantage similar to Particle Swarm Optimization Algorithm. Shuffled Frog Leaping Algorithm has
a lot of strong points,such as few parameters, easy to implement and fast convergence Shuffled Frog Leaping
Algorithm was applied by all kinds of intelligent optimization systems. For example, Mgmt made use of the Shuffled
Frog Leaping Algorithm in the water distribution optimization system in 2003 and Alireza applied th e SFL algorithm
in the mixed linear model series in 2007. |
 |
| The step by step algorithm are as follows: : |
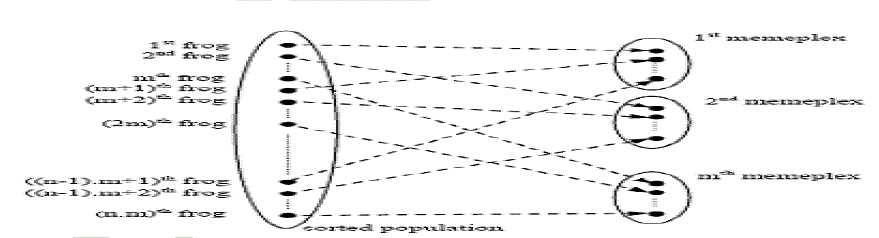
| Step1: Create an initial population of P frogs generated randomly. SFLA Population =[X1,X2,…,Xp]p×n Where, P=m×n,
N is the number of distributed generation , m is the no of memplexes and n is the number of frogs in memplex. |
| Step 2: Sort the population increasingly and divide the frogs into m memplexes each holding n frogs such that P=m×n. |
| Step 3: Within each constructed memeplexes, the frogs are effected by other frogs' ideas; hence they experience a metaheuristics
evolution. Me-metic evolution improves the quality of the meme of an individual and enhances the individual
frog’s performance towards a goals. Below which are details of me-metic evolution for each memeplexes: |
| Step 4: Check the convergence. If the convergence criteria are satisfied stop, otherwise consider the new population set as the
initial population and return to the step2. The best solutions is found in the search process is considered as the output
results of the algorithm. The flowchart of the SFLA is illustrated in Fig. 5. |
 |
RESULT AND DISCUSSION |
| The objective function of the RPL minimization problem is formulated by introducing penalty factors for voltage,
transformer MVA, and transmission line limit violations. These penalty factors are added to the total real power
loss in the system the cost function is modified by reciprocal of VSL to the real power loss. The optimization
process is taken with the help of MSFLA with BFAM. With only transformer taps as control variables along
with the corresponding optimized loss and VSL are given in Table 1. It is seen that the VSL value has
improved, although the real power loss has raised in transmission line marginally. However, the sum of real power
loss and the reciprocal of Voltage stability limit has reduced, when the multi-objective function is considered.
With the aim of till reducing the objective function the UPFC variables are evaluated by the optimized transformer
tap positions obtained in previous step. Optimized values of upfc location and injection voltage with transformer
tap values fixed shown in table 2. The UPFC is connected at the left-hand-side bus as per line notation.. In the case
of SFLA, the line at which UPFC should be connected is decided randomly out of 30 lines selected in the starting
stage. the SFLA, number of lines in which UPFC is to be connected also becomes a control variable along
with others. The UPFC is connected in all the 30 lines, considering one at a time.. The best location and the
UPFC injection voltage in each succession of linearization are retained. The overall cost function can still be
reduced by simultaneous optimization of UPFC location and its variables along with transformer taps The
numbers of variables is 15 , i.e., 12 transformer tap settings values, and three UPFC variables. |
| With SFLA, which comes in 14, the location of UPFC device cannot be taken. Optimized taps and upfc
parameters for real power loss minimization & voltage stability limit shown in table 3. The optimization algorithm
remains the same. It is shows that, the value of Voltage stability limit has improved considerably, though at the
cost of deteriorated loss reduction. The P-V curves for the three optimized schemes are shown in Fig.8. |
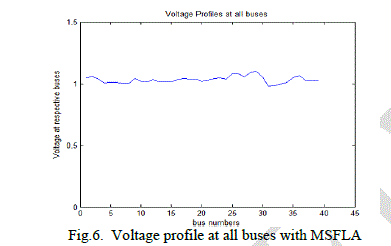
| In the fig 6, it shows the graph of Voltage with respect to buses Vs Bus numbers. Analysis of voltage levels in bus
numbers within per unit value. It is observed that all the bus voltages remain within the limits, and the
generator buses maintain their specified voltages when the optimized variables are used. |
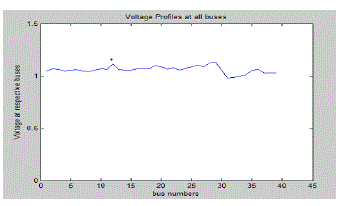
| In the fig 7, it shows the graph of Voltage with respect to buses Vs Bus numbers. Analysis of voltage levels in bus
numbers within per unit value. The magnitude of voltage (with simultaneous optimization), obtained with
MSFLA&BFAM optimization is shown in figure6&7. It is observed that all the bus voltages remain within the
limits, and the generator buses maintain their specified voltages when the optimized variables are used. |
CONCLUSION |
| This paper presented an modified Shuffle Leap Frog Algorithm is used for allocating the transformer taps, and UPFC with
a view to minimize the real power loss and improve VSL of a system simultaneously. The performance of the
Shuffled Frog Leap algorithm for solving multi-objective that is real power loss minimization and Maximization of
Voltage stability limit is demonstrated using IEEE-39 Radial bus system. The results shows that the MSFLA algorithm which is
used for allocating transformer taps, and control of UPFC with This paper presented an modified Shuffle Leap Frog Algorithm is used for allocating the transformer taps, and UPFC with
a view to minimize the real power loss and improve VSL of a system simultaneously. The performance of the
Shuffled Frog Leap algorithm for solving multi-objective that is real power loss minimization and Maximization of
Voltage stability limit is demonstrated using IEEE-39 Radial bus system. The results shows that the MSFLA algorithm which is
used for allocating transformer taps, and control of UPFC with |
Tables at a glance |
 |
 |
 |
 |
| Table 1 |
Table 2 |
Table 3 |
Table 4 |
|
Figures at a glance |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
 |
 |
 |
 |
| Figure 5 |
Figure 6 |
Figure 7 |
Figure 8 |
|
References |
- P. Ristanovic, “Successive linear programming based OPF solution,” Optimal Power Flow: Solution Techniques, Requirements andChallenges,IEEE Power Eng. Soc., pp. 1–9, 1996.
- D. Sun et al., “Optimal power flow by newton approach,” IEEE Trans. Power App. Syst., vol. PAS-103, no. 10, pp. 2864–2875, Oct. 1984.
- S. Granville, “Optimal power dispatch through interior pont methods,” IEEE Trans. Power Syst., vol. 9, no. 4, pp. 1780–1787, Nov. 1994.
- G. Torres and V. Quintana, “An interior point method for non-linear optimal power flow using voltage rectangular coordinates,” IEEETrans.Power Syst., vol. 13, no. 4, pp. 1211–1218, Nov. 1998.
- J. L. Martinez Ramos, A. G. Exposito, and V. Quintana, “Transmission loss reduction by interior point methods: implementation issues and practical experience,” Proc. Inst. Elect. Eng., Gen., Transm.,Distrib., vol. 152, no. 1, pp. 90–98, Jan. 2005.
- M. Noroozian, L. Angquist, M. Ghandhari, and G. Anderson, “Use of UPFC for optimal power flow control,” IEEE Trans. Power Del., vol. 12, no. 4, pp. 1629–1634, Oct. 1997.
- G. Glanzmann and G. Andersson, “Coordinated control of FACTS devices based on optimal power flow,” in Proc. 37th Annu. NorthAmer.PowerSymp., Ames, IA, Oct. 23–25, 2005.
- V. Ajjarapu and C. Christy, “The continuation power flow: a tool for steady state voltage stability analysis,” IEEE Trans. Power Syst., vol. 7, no. 1, pp. 416–423, Feb. 1992.
- F. Milano, C. A. Canizares, and A. J. Conejo, “Sensitivity-based security- constrained OPF market clearing model,” IEEE Trans. Power Syst., vol. 20, no. 4, pp. 2051–2060, Nov. 2005.
- J. Yuryevich and K. P. Wong, “Evolutionary programming based optimal power flow algorithm,” IEEE Trans. Power Syst., vol. 14, no. 4, pp. 1245–1250, Nov. 1999.
- A. A. A. Esmin, G. Torres, and A. C. Z. de Souza, “A hybrid particle swarm optimization applied to loss power minimization,” IEEETrans.Power Syst., vol. 20, no. 2, pp. 859–866, May 2005.
- M. Eusuff, K. Lansey, F. Pasha; “Shuffled frog-leaping algorithm: a memetic meta-heuristic for discrete optimiza-tion”, EngineeringOptimization, 2006, Vol. 38, No. 2, pp.129–154.
|