International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Optimal Path Search with User-Defined Queries

Sravani Adusumilli1*, S Ravi Kishan2
  1. Student, Dept. of Computer Science and Engineering, Velagapudi Ramakrishna Siddhartha Engineering College Vijayawada, India
  2. Associate Professor, Dept. of Computer Science and Engineering, Velagapudi Ramakrishna Siddhartha Engineering College Vijayawada, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Nodes Most navigational apps, nowadays, merely find point-to-point route specifics and cannot handle intricate search scenarios. A more elaborate navigation method that has a route search with effective routes for complex queries in heterogeneous environments, while dealing with uncertainties with regard to geographic entities was developed using Batch Forward Search (BFS) algorithm. Although BFS formulated a way to integrate these arbitrary constraints into a specific route search, they may not be useful to the user. In realistic scenarios, the navigational service provider should consider additional complicating factors such as the working hours of the entities to be visited, type of service those entities cater to and possible restrictions on the order by which the entities may be visited. We extend the Batch Forward Search algorithm with Temporal Approximation Algorithm to handle temporal constraints over route queries. We believe that proposed method will be effective and more elaborative compared to prior approaches.

 

Keywords
BFS, Constraints, Routes, Temporal, Queries

INTRODUCTION
In general people desire to travel less distance but they wish to cover all the places and satisfy the order constraints. The traditional approaches incur a significant amount of repeated computations, and thus are not scalable to large datasets. Top route service providers such as Google City Tours (citytours.googlelabs.com), Yahoo Travel (travel.yahoo.com) have provisions for users to search and share trips, which unfortunately, cannot answer optimal route queries or can’t include the constraints defined by the user. So a novel and efficient approach is required.
The Point of interest (POI) sequences also called as route collections obtained from GPS/GIS enabled devices helps users reach their destinations faster by using the sorted routes information obtained from the route collections. This sorting process involves path query evaluation on large disk of route collections that are frequently updated. Updates involve additions and deletions of routes. A route collection can be trivially transformed to a graph; hence, path queries can be evaluated using standard graph search techniques. Such methods follow one of two methods. The first employs graph traversal methods, such as depth first search (DFS). The second compresses the graph’s transitive closure, which contains reach ability information, i.e., whether a path exists between any pair of nodes. While transitive closure techniques are the fastest, they are mostly suitable for data sets that are not frequently updated, or when the updates are localized, since they require expensive pre-computation. On the other hand, DFS are easily maintainable, but are slow as they may visit a large part of the graph.
For a given a set of spatial points each categorical information, e.g., restaurant, pub, etc., the optimal path query finds the shortest path that starts from the query point (e.g., a home or hotel), and covers a user-specified set of categories (e.g., pub, restaurant, museum). The user may also specify partial order constraints between different categories, e.g., a restaurant must be visited before a pub.In the proposed system the query contains two parameters: a starting point q, and a directed acyclic graph GQ called the visit order graph. Each vertex in GQ corresponds to a category and each edge ?C; C′? indicates that a point of category C must be visited before another of category C′. Prior approaches used a Greedy algorithm to answer the optimal route query. We use propose two efficient techniques Backward search and Forward search to find optimal path query. The first one computes the optimal route from the last point to the first, while the other follows the first-to-last order of points
The navigational service provider should consider additional complicating factors such as the working hours, type of service and possible restrictions on the order by which the entities may be visited. We refer to such factors as temporal constraints. Incorporation of such temporal constraints in our spatial scenario leads to a new spatial-temporal approach to route queries. For that we extend the Batch Forward Search algorithm with a new method to handle temporal constraints over route queries. Results are effective and more elaborative compared to prior approaches and an implementation of the proposed approach validates our claim.
The objective of the project is to find a optimal route query which considers all the necessary constraints defined by the user. The constraints may be arbitrary constraints such as a ATM machine should be visited before Restaurant or a temporal constraint such as working hours of a restaurant

RELATED WORK
Bouros and Panagiotis, et al [1] consider path queries on frequently updated route collections given a route collection and two points ns and nt, a path query returns a path, i.e., a sequence of points that connects ns to nt. This work targets path query evaluation on large disk resident route collections that are frequently updated. Updates involve additions and deletions of routes. A route collection can be trivially transformed to a graph; hence, path queries can be evaluated using standard graph search techniques. Such methods follow one of two paradigms. The first employs graph traversal methods, such as depth first search (DFS) [3]. The second compresses the graph’s transitive closure, which contains reach ability information, i.e., whether a path exists between any pair of nodes. Both paradigms have both strengths and weaknesses. Here graph traversal techniques like RTS and LTS. The route traversal search (RTS) in [2], expands the search considering all successor nodes in the route, while link traversal search (LTS) considers only the next link on the nodes of the route collection. Route Traversal Search with Transitions (RTST) uses the T -Index in addition to R-Index to captures transitions among routes allowing earlier termination [1].Link Traversal Search with Transitions (LTST) has a stronger condition based on the T -Index. The LTS-k algorithm forgoes the high storage and maintenance cost of T -Index and features a tunable termination condition.
Zhao and Geng, et al [4] discuss about the path search using the mobile networks. In a mobile environment the information and query services are based on the continuous mobile query processing or continuous k nearest neighbor (CKNN), which finds the locations where interest points or interest objects change while mobile users are moving. These locations are known as “split nodes.” All of the existing works on CKNN divide the query path into segments, which is a segment of road separated by two intersections, and then, the process to find split nodes is applied to each segment. Processing each segment is not possible so here we use Voronoi diagram fo CKNN. Since it doesn’t divide the path into segments it achieves better performance. One of the most prominent and growing applications of mobile information services is mobile navigation [5], due to the increase of traffic loads and the complexity of road connections. The most common search is KNN search [6]. The problem of KNN has also been addressed in other areas, including data mining and industrial electronics [7].In order to find split nodes, all existing CKNN approaches divide the query path into segments, find KNN results for the two terminate nodes of each segment, and then, for each segment, find the split nodes. One segment of the path starts from an intersection and ends at another intersection. For every segment, a KNN process is invoked to find split nodes for each segment.
A Voronoi diagram is a special kind of decomposition of a metric space determined by distances to a specified discrete set of objects in space [8]. Given a set of points S, the corresponding Voronoi diagram will be generated. Each point s has its own Voronoi cell V (s), which consists of all points closer to s than to any other points. The border points between polygons are the collections of the points with equations of distance to shared generators.
Chen and Haiquan, et al [9] propose a novel spatial query type, the multi-rule partial sequenced route (MRPSR) query, which will help the user with good trip planning efficiently with user defined rules. The MRPSR query provides a unified framework that subsumes the well known trip planning query (TPQ) and the optimal sequenced route (OSR) query. The difficulty in answering MRPSR queries lies in how to integrate multiple choices of points-of-interest (POI) with travelling rules when searching for satisfying routes. By keeping the traveling rules into an activity-on-vertex network, we utilize topological sorting [10] to integrate travelling rules with multiple choices of POIs and study the solvability of MRPSR queries.
The Nearest Neighbor-based Partial Sequence Route query (NNPSR) algorithm. The NNPSR algorithm uses activity-on-vertex networks to guide the search to retrieve a near-optimal route satisfying all the traveling rules in road networks. Here the graph has an edge <i, j> if and only if category i is an immediate prerequisite for category j in one of the rules. The graph is named as Activity on Vertex (AOV) network [15]. The first step is to list out a vertex in the network that has no predecessor. Then the second step is to delete this vertex and all edges leading out it from the AOV. These two steps are repeated until all the vertices have been listed.
Integrating NNPSR with the Light Optimal Route Discoverer (LORD) algorithm [11] to create NNPSR-LORD that further reduces the trip distance based on the NNPSR algorithm. LORD is a threshold-based algorithm and requires less memory space compared with Dijkstra’s algorithm. First step is issue consecutive nearest neighbor queries to find the greedy route that follows the given POI sequence from the starting point. Keeps a variable threshold value (T) whose value reduces after the each iteration and it discards all the POIs whose distances to the starting point are more than (T).
Advanced A* Search-based Partial Sequence Route query (AASPSR (k)) algorithm [12]. AASPSR (k) takes advantage of the location of the destination as well as travelling rules to generate an efficient trip plan in road networks. Here we use the sum of costs of source to initial point and destination to initial point to retrieve the point of interests (POI) The minimum cost among all will be taken into the route list and will update the list Process will repeat until all the user selected categories are covered in the trip plan.
Tao and Yufei, et al [13] discuss the continuous monitoring, when interest points or interest objects are changed due to the movement of mobile users, the mobile users are notified of these changes. These are known as split nodes. This method focuses on efficiently identifying split nodes The CKNN can be defined as search where, given a moving query point, its predefined moving path, and a set of candidate interest points. The objective is to find the point on the way where KNN change. A continuous nearest neighbor (CNN) query retrieves the nearest neighbor (NN) of every point in a line segment q = [s, e]. In particular, the result contains a set of <R, T> tuples, where R (for result) is a point of P, and T is the interval during which R is the NN of q.
Zhao and Geng, et al [14] discuss the concept of path-based k nearest neighbour (pkNN) is introduced. Given a set of candidate interest objects, a query point, and the number of objects k, pkNN finds the shortest path that goes through all k interest objects with the minimum shortest distance among all possible paths. pkNN is useful when users would like to visit all k interest objects one by one from the query point, in which pkNN will give the users the shortest path. Traditional queries in spatial databases are range search [15] and k nearest neighbour (NN) (kNN) search [16]. Range search is to find all interest objects within a predefined range, while kNN search is to find k interest objects which are the closest to the query point. Both range and kNN searches provide users the candidate set of interest points and allow users to choose any one in the set because they have been previously filtered by users’ conditions

PROPOSED ALGORITHM
A. Algorithm Batch Forward search:
InitBFS (q, GQ)
Input: q, GQ: query start point and visit order graph respectively
Output: the optimal route that satisfies the query
1: Use a greedy algorithm to obtain a route rg
2: Initialize threshold to length (rg)
3: Retrieve the set CS of points within distance to q, whose categories appear in GQ
4: Initialize route set R1 to empty
5: Initialize all elements of Ω to Unknown
6: Partition points in CS into clusters, such that points in the same cluster belong to the same category, and are close to each other
7: Call BFS (q, GQ, {q}, {q}, θ), and return the only route in its result set.
BFS (q, G, P, R, θ)
Input:
• q: query start point
• G: sub-graph of GQ containing only unvisited categories
• P: tail cluster of the current cluster-route
• R: set of shortest routes from q to each point in P, only includes routes with length shorter than θ
• θ :length of a known route that satisfies the query
Output: the set of all optimal routes that starts at a point in P, and covers all categories in G.
1: Let V be the set of categories in G, category CP be the category of all points in P, and set V′= V \ {CP}.
2: Construct new sub-graph G′ by removing Cp and all related edges from G
3: if ΩP; V ?= Unknown then return ΩP; V
4: if V contains a single category CP then return a set of routes, each containing a single point in P
5: Compute the minimum distance from P to its nearest cluster of each category C ∈ V, and set dmax to the maximum value of these distances
6: if mindist (q, MBRP) +dmax ≥ θ then set ΩP; V to Invalid, and return Invalid.
7: for each cluster P′ ∈ CS in increasing order of mindist (MBRP, MBRP′) Do
8: if adding P′ to the current cluster route violates G then Continue
9: Call R′=FSJoin (q, G, R, P′, θ)
10: Recursively call ΩP′; V′ = BFS (q, G′, P′, R′, θ)
11: Call BSJoin (q, G, P′, V′, P) and merge results to ΩP; V
12: if R ?= Φ then
13: Compute routes r1 ∈ R, r2 ∈ ΩP; V such that the end point of r1 is the start point of r2, and length (r1 ∈ R) +length (r2) is minimized
14: if length (r1) +length (r2) < then Update θ and CS
Then the BFS algorithm is extended with MED Algorithm to satisfy the temporal constraints defined by the user
B. Temporal Approximation:
MED ((s, t,Q,C),D,?)
Input: Start location s, target location t, search queries
Q1, . . . ,Qm ordered according to C, a dataset D, an order < over D
Output: The next object to be visited
1: if Q is empty then
2: return t
3: Computing expected distances
4: curr ← s
5: for i = 1 to m do
6: found ← false
7: while not found do
8: if Ai = Φ then
9: return “the route cannot be completed”
10: o ← argmin(o∈Ai(dist(curr, o) + E[o])
11: provide o to the user and get a feedback
12: curr ← o
13: if o does not satisfy Qi then
14: remove o from Ai
15: else
16: found ← true
C. Description:
To overcome the drawbacks of the existing route query systems, the proposed system is includes the user defined constraints in the queries. The query contains two parameters: a starting point q, and a directed acyclic graph GQ called the visit order graph. Each vertex in GQ corresponds to a category and each edge ?C; C′? indicates that a point of category C must be visited before another of category C′. Prior approaches used a Greedy algorithm to answer the optimal route query first finds the nearest neighbor of q that is allowed to be visited right after q according to GQ to be added to the route. We propose several efficient solutions to the general-case optimal route query. Temporal is defined as something "lasting for a relatively short time". Most navigational apps, nowadays, merely find a point-to-point route and cannot handle intricate search scenarios. We introduces a more elaborate navigation method that has a route search with effective routes for complex queries in heterogeneous environments, while dealing with uncertainties with regard to geographic entities.
In a route-search, a user specifies their requirements in the form of a query, and the main task is to find a route that goes via geographical objects while satisfying the search specifications. For example, consider a tourist in a foreign city says Hyderabad, wants to plan a route from their current location to some destination, via four types of entities:
? A Fuel Station,
? An ATM,
? A Vegetarian Restaurant.
Although prior approaches formulated a way to integrate these arbitrary constraints into a specific route search, they may tend not to be useful to the user, Such as the route will go via a restaurant that is not really vegetarian. In realistic scenarios, the navigational service provider should consider additional complicating factors such as the working hours of the entities to be visited, type of service those entities cater to and possible restrictions on the order by which the entities may be visited. We refer to such factors as temporal constraints. Incorporation of such temporal constraints in our spatial scenario leads to a new spatial-temporal approach to route queries. Propose to extend Batch Forward Search algorithm with Temporal Approximation Algorithm over Route queries to handle temporal constraints over route queries.
The proposed system is implemented in the following steps:
1. Places repository setup: This phase involves accumulation of various locations information with respect to latitude(x-coordinate) and longitude(y-coordinate) in the form of SQL queries.
2. Route repository setup: This phase involves specifying various combination of intra locations information along with distances within the confines of a boundary in the form of SQL queries.
3. Querying interface: This phase involves an automated selection of source and destinations for all possible route estimations along with a best route.
4. Data base to dataset conversion: This phase involves conversion database to comma separated values (CSV) data set implementation for optimal route mining queries.
5. Map entities plotter c places with paths either direct/indirect: This phase involves plotting the places on a predefined map interface along with paths in the form of weights or distances between them.
6. Existing graph simulation (DFS) with time resources: In this phasetime comparison for the implementation of existing approaches is done.
7. Batch forward search algorithm implementation on route indexes and selected nodes: In this phase the Graph traversal implementation of best edges with more results on a selected arbitrary constraint’s selection is vital.
8. Query results with time resources: Time comparison for the implementation of proposed approaches.
9. Spatio-Temporal Relations setup and retrieval: This phase concentrates on establishing semantic retrievals for all arbitrary constraints. And it requires auto retrieval of temporal data pertaining to a retrieved arbitrary constraint from step 7

PSEUDO CODE
Step 1: Initially take a threshold route length value
Step 2: Points neighbouring to q are arranged into clusters of categories
Step 3: Construct a sub graph G’ such that all the edges and categories which are not required are removed
Step 4: Compute the minimum distance from P to its nearest cluster of each category C ∈ V, and set dmax to the maximum value of these distances If mindist(q, P )+dmax ≥ θ then set d(P,V) to Invalid, and return Invalid
Step 5: For each cluster P′ ∈ C in increasing order of mindist (P , P′ ) if adding P′ to the current cluster route violates G then return invalid.
Step 6: Else Compute routes r1 ∈ R, r2 ∈ d(P,V) such that the end point of r1 is the start point of r2, and length(r1 ∈ R) +length(r2) is minimized. If length (r1) +length(r2) < then Update θ Else goto step 5 and repeat the process

SIMULATION RESULTS
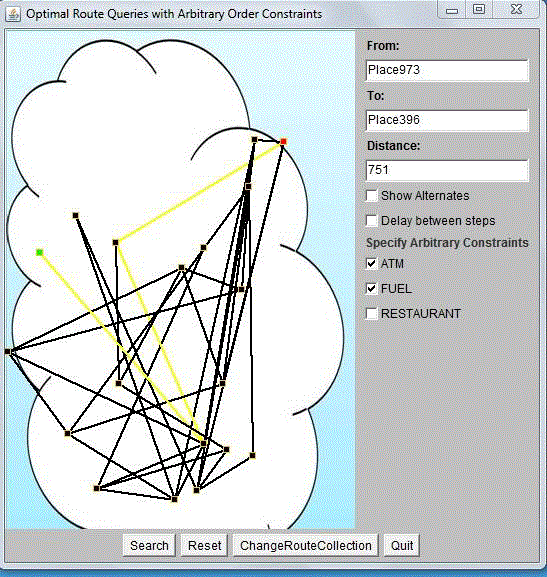
The simulation studies involve the deterministic small route collection nodes as shown in Fig.2. The proposed energy efficient algorithm is implemented with NETBEANS. When selecting the required database path search system will be opened as shown in fig 2. Based on his desire he can select them using the checkboxes shown in fig 2. We can select the source and destination points by selecting the points shown in the map. When the source and destination points are selected we can run the querying interface. The source is indicated with green colour and destination is indicated with red colour, the path is highlighted when the query system is run as shown in fig 2.
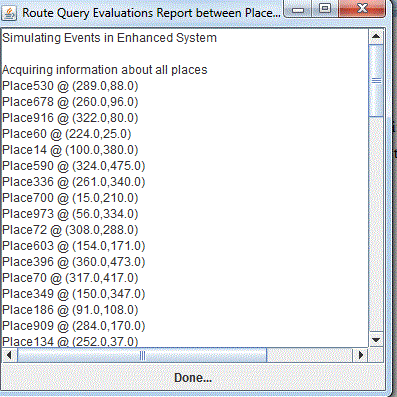
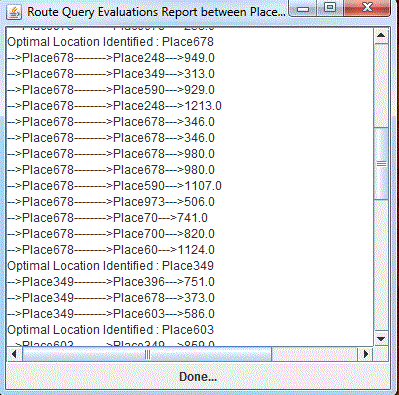
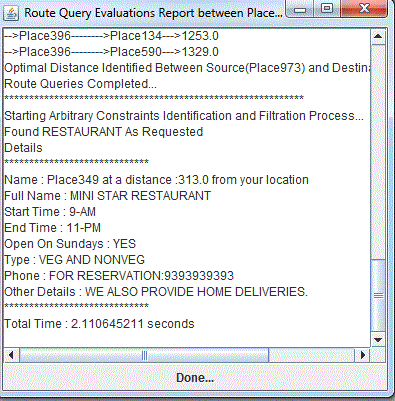
Along with this, the output will be shown in figure 4 which shows or explains how the different points in the map are selected and how optimal path is found. The figure 3 shows information of many points which are present in the path. If there are any constraints such as a restaurant or petrol bunk should be selected in the route between source and destination is selected, then its information is obtained here as shown in fig 5. If there are no selected constraints in the route selected it displays that there are no arbitrary constraints identified.

CONCLUSION AND FUTURE WORK
The simulation results showed that the proposed algorithm gives information about the user defined constraints and optimal location efficiently. We developed a novel method to provide search engine query which satisfies the user defined constraints. Here the combination of two algorithms Batch Forward Search algorithm (BFS) and temporal approximation algorithm is used, which effectively implements the optimal query system. The user can define their constraints arbitrary or temporal. With this new approach, the users not only get the optimal route but also get route based on their requirement. We believe that the proposed method will resolve the key issues regarding the route queries systems with the constraints. In future the need for developing an optimal route query system which can handle more number of categories to be visited should be developed. Here in this, if there is no category or place found present in the selected route it displays the information such as there no places required in the selected route. So there is a need for an optimal route query system to give the alternative best path which consists of the selected route in between the route from source to the destination.

Figures at a glance
Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4

References















/td>