International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Optimal Top-K Queries Computing: Sampling and Energetic Development Approach

Marthe Ranjani A, Mrs.Ananthi M
  1. PG Scholar, Dept of IT, Sri Sairam Engineering College, India
  2. Associate Professor, Dept of IT, Sri Sairam Engineering College, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

An effective query processing plays an significant role in the unsure data streams. Particularly, manifold top-k queries processing on uncertain data streams obtained from large applications of several fields such as sensor network monitoring and internet traffic control requires periodic execution of queries and sharing results among them. The system that monitors uncertain events in such data streams manipulates the top-k queries. Here the problem is that existing systems were not planned to allow query results sharing which in turn leads to high computation cost and inaccurate response from the system. To overcome these issues (Queries results sharing), the proposed system using a sampling algorithm for sample the top possible worlds from well-known possible worlds based on their high probability. Therefore, proposed system uses an optimal dynamic programming approach that split the multiple queries into number of groups. Then the query groups are scheduled and planned for sharing results to yield minimum computation cost. Accordingly, a faster greedy algorithm is used to reduce the time and storage space of the top-k queries based on the greedy rule. Thus the proposed approach allows sharing computation among multiple top-k queries and generates best plan of query execution.



INTRODUCTION
There are many applications in which data naturally occur in the form of a sequence of values, for example feeler data, economic tickers, online auctions, Internet traffic, web usage logs, and phone call records. These data can be modeled as data streams, which are limitless data sets produced incrementally over time. Often, the error may occur due to the following reason such as monitoring equipment, individual worker mistakes, and interference in data transfer, these data may be unfinished, untrustworthy, or deafening, with the result that uncertainty is inherent in these data stream applications. A great deal work has focused on unsure data streams and the semantics of possible worlds has been widely adopted in dealing with them. A possible world is a possible instance amalgamation of tuples, usually within a sliding window. For a given time stamp, the tuples in the sliding window result in a number of possible worlds, whose number exponentially increase with the number of tuples in the sliding window. The applications listed above classically issue a large number of monitoring queries. These are queries that are registered to the system, and they are executed occasionally. An important subclass of these queries is top-k queries. For example, traffic monitoring applications typically wish to determine the top-k speeds of cars that pass through a control point, and volcano monitoring applications observe top-k readings from sensors that produce uncertain data streams. We discuss traffic monitoring in more detail below. Preceding work has measured executing these queries individually, but there are significant benefits to handling them collectively by exploiting similarities. This is the eminent multiquery optimization problem, which is known to be very solid in relational DBMSs. This trouble is particularly difficult over unsure data streams. Also, the maximum number possible world combinations can be increase the processing time if the probability is not suitable to group of top-k queries. To overcome these issues, the proposed system using a sampling algorithm for sample the top possible worlds from well-known possible worlds based on their high probability. Consequently, proposed system uses an optimal dynamic programming approach that split the multiple queries into number of groups. Then the query groups are scheduled and planned for sharing results to yield minimum computation cost. Consequently, a faster greedy algorithm is used to reduce the time and storage space of the top-k queries based on the greedy rule. Thus the proposed approach allows sharing computation among multiple top-k queries and generates best plan of query execution.

RELATED WORK
In the existing system top-k queries are processed using optimal dynamic programming solution and greedy algorithm [1] Queries are processed proficiently using greedy algorithm. Outcomes are not shared which leads to high working out cost. In the other paper top-k queries using Sliding-window with Maintain-CSQ and Batch update algorithm in the uncertain data streams [2]. But it only applied on simple data model and could not obtain predictable better performance (time, storage, computation cost) in the complex data model. In another paper the top-k queries are processed using Deterministic exact Algorithm and Randomized method in the continuous uncertain data streams [3]. Query processing efficiency linearly increased because of independent probabilistic uncertain data streams. The disadvantage is that limited scalability and communication cost is high because of it supported only independent probabilistic uncertain data streams.

PROPOSED WORK
An efficient solution framework for top-k query evaluation. The applications compute queries that involve joining and aggregating multiple inputs to provide users with the top-k results. In order to reduce the possible worlds a sampling algorithm is used. In order to make the system more optimal a dynamic programming solution is been used to reduce the time, space complexity and the cost. A Faster Greedy Algorithm is used to reduce the storage space. It executes the multiple top-k queries based on the greedy rule.
The advantages are possible worlds are sampled that enlarged query processing speed, query executing cost is reduced using optimal dynamic programming method, execution time condensed using the Faster Greedy Algorithm also query processing storage space is reduced, multi k-queries are sampled efficiently for future work ,accuracy increased.

IMPLEMENTATION
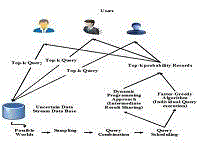
Preliminary stage of the paper is to sample the possible worlds from the number of possible worlds based on the lower and upper probability and to combine the top-k query groups into single query group based on combination rule. Occasionally, the top-k queries may not be used all possible worlds’ probability because of the top-k limitation. So the limited possible worlds can be eliminated use using sampling method l ≤ P(PW) ≤u where l-represent lower probability constraint, urepresent upper probability constraint P(PW)- represent probability of possible worlds. Top-k Queries are combined into query groups and the query groups are combined into no sharing between them. The Top-k queries are divided into number of groups. The query groups are joint until no pair of groups occurred between them i.e. kmaxi≥kmaxj and i<j and fi<fj , where k- represent top value f- represent frequency upper bound , i-represent the first query group, j- represent next query group. This process is implementation is shown in the figure 2 and 3.

CONCLUSION
The top-k queries are always frequently executed. The queries may take more storage and time if every query is executed individually. So, to prevent this issue the query optimization is utilized. The two execution steps of the proposed method show that the best query optimization is achieved. The first step is sampling the possible worlds successfully to reduce topk computation of every tuples. The second is combining almost all query groups into very less query group that can be utilized to share the midway results between them.

Figures at a glance
Figure 1 Figure 2 Figure 3
Figure 1 Figure 2 Figure 3

References