Keywords
|
| Transportation Time, processing time, elapsed time, Branch and Bound. |
INTRODUCTION
|
| Flow shop scheduling models are effective tools for management that can be utilized for modelling many service and production processes such as continuous production systems. In some flow shop scheduling problems, each manufacturing centres has more than one machine, each job is started through the first machine and then goes to next machine in order, ending up with the last machine. In flow shop scheduling problems, all machines are arranged in constant series. The main objective is to find the best possible schedule and sequence for jobs in order to minimize the makespan. A flowshop scheduling problem has been one of classical problems in production scheduling since Johnson [6] proposed the well known Johnson’s rule in the two-stage flowshop makespan scheduling problem. Yoshida and Hitomi [11] further considered the problem with setup times. Yang and Chern [10] extended the problem to a twomachine flowshop group scheduling problem. Maggu and Dass[9] introduced the concept of equivalent job for a jobblock when the situations of giving priority of one job over another arise. Kim, et al.[7] considered a batch scheduling problem for a two-stage flowshop with identical parallel machines at each stage. Brah and Loo [1] studied a flow shop scheduling problem with multiple processors. Futatsuishi, et al. [4] further studied a multi-stage flowshop scheduling problem with alternative operation assignments. |
| Lomnicki [8] introduced the concept of flow shop scheduling with the help of branch and bound method. Further the work was developed by Ignall and Scharge [5], Chandrasekharan [3] , Brown and Lomnicki [2], with the branch and bound technique to the machine scheduling problem by introducing different parameters. Practically scheduling problem depends upon the significant factors namely, Transportation time. The transportation times (loading time, moving time and unloading etc.) from one machine to another are also not negligible and therefore must be included in the job processing. However, in some application, transportation time have major impact on the performance measures considered for the scheduling problem so they need to considered separately. In this paper we consider a two-stage flowshop scheduling problem including Transportation time with the help of branch and bound method. Branch and bound is an exact method usually used in scheduling problems to find optimal solutions. This method requires three components: a lower bound (LB), an upper bound and a branching strategy. Branch and bound provides a systematic enumeration procedure that considers bounds on the objective function for different subsets of solutions. Subsets are eliminated when their lower bound is dominated by the bound of other subset. The procedure is repeated until the search tree is exhausted and the optimal solution is found. The given method is very simple and easy to understand. Thus, the problem discussed here has significant use of theoretical results in process industries. |
ASSUMPTIONS
|
| i. No passing is allowed. |
| ii. Each operation once started must performed till completion. |
| iii. Jobs are independent to each other. |
| iv. A job is entity, i.e. no job may be processed by more than one machine at a time. |
| v. Σpi=1, Σqi=1, 0≤pi≤1 and 0≤qi≤1 |
NOTATIONS
|
| We are given n jobs to be processed on two stage flowshop scheduling problem and we have used the following notations: |
| ai : Processing time for ith job on machine A |
| bi : Processing time for ith job on machine B |
| pi : Probability associated with processing time ai. |
| qi : Probability associated with processing time bi. |
| S0 : Optimal sequence |
| ti : Transportation time of ith job from machine A to machine B |
| Ai : Expected processing time of ith job on machine A |
| Bi : Expected processing time of ith job on machine B |
| Jr : Partial schedule of r scheduled jobs |
| Jr′ : The set of remaining (n-r) free jobs |
MATHEMATICAL DEVELOPMENT
|
| Consider n jobs say i=1, 2, 3 … n are processed on two machines A & B in the order AB. A job i (i=1,2,3…n) has processing times ai & bi associated with their respective probabilities pi and qi on each machine A & B respectively. Let Ai be the expected processing time on machine A and Bi be the expected processing time on machine B. Let ti be transportation time of ith job from machine A to machine B. The mathematical model of the problem in matrix form can be stated in tableau-1 : |
ALGORITHM
|
| Step 1: Calculate Expected processing time Ai = ai x pi and Bi = bi x qi |
| Step 2: (i) Gi = Ai + ti and (ii) Hi = Bi + ti |
| Step 3: Calculate |
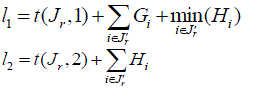 |
| Step 4: Calculate |
| l=max(l1, l2 ) |
| We evaluate l first for the n classes of permutations, i.e. for these starting with 1, 2, 3………n respectively, having labelled the appropriate vertices of the scheduling tree by these values. |
| Step 5: Now explore the vertex with lowest label. Evaluate l for the (n-1) subclasses starting with this vertex and again concentrate on the lowest label vertex. Continuing this way, until we reach at the end of the tree represented by two single permutations, for which we evaluate the total work duration. Thus we get the optimal schedule of the jobs. |
| Step 6: Prepare in-out table for the optimal sequence obtained in step 6 and get the minimum total elapsed time. |
NUMERICAL EXAMPLE
|
| Consider 4 jobs 2 machine flow shop problem whose processing time of the jobs on each machine is given in tableau-2 |
| Our objective is to obtain optimal schedule for above said problem. |
| Solution:As per Step1: The expected processing time as in tableau-3 |
| Step2: Calculated values are as in tableau-4 |
| Step3: Calculate |
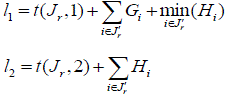 |
| For J1 = (1).Then J′(1) = {2,3,4}, we get l 1 = 77 , l 2 = 76 |
| LB(1) 1 2 l ? max(l , l ) =77 |
| Similarly, we have LB(2)= 79, LB(3)= 81, LB(4)= 88 |
| Step 3 & 4: |
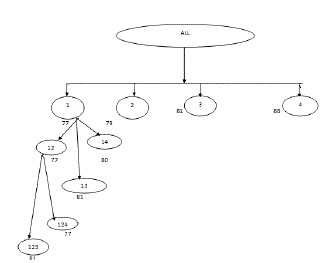
| Now branch from J1 = (1). Take J2 =(12).Then J′2={3,4} and LB(12) = 77 Proceeding in this way, we obtain lower bound values as shown in the tableau- 5 |
| Step 5 : |
| Therefore the sequence S1 is 1-2-4-3 and the corresponding in-out table for sequence S1 is as in tableau-5: |
| And the tree is as follows: |
| Hence the total elapsed time is 59 units |
REMARKS
|
| The study may further be extended by considering various parameters such as break down interval, due date, mean weightage time etc. |
Tables at a glance
|
 |
 |
 |
 |
 |
| Table 1 |
Table 2 |
Table 3 |
Table 4 |
Table 5 |
|
Figures at a glance
|
 |
| Figure 1 |
|
References
|
- Brah, S.A. and Loo, L.L., “Heuristics for Scheduling in a Flow Shop with Multiple Processors,”European Journal of Operation Research, Vol. 113, No.1, pp.113-122, 1999.
- Brown, A.P.G. and Lomnicki, Z.A., “Some applications of the branch and bound algorithm to the machine scheduling problem”, Operational Research Quarterly, Vol. 17, pp.173-182, 1966.
- Chander Shekharan, K, Rajendra, Deepak Chanderi, “An efficient heuristic approach to the scheduling of jobs in a flow shop”, European Journal of Operation Research Vol. 61,pp. 318-325, 1992.
- Futatsuishi, Y., Watanabe, I., and Nakanishi, T., “A Study of the Multi-Stage Flowshop Scheduling Problem with Alternative Operation Assignments,”Mathematics and Computers in Simulation,Vol. 59, No. 3, pp.73-79, 2002.
- Ignall, E. and Schrage, L., “Application of the branch-and-bound technique to some flowshop scheduling problem”, Operations Research, Vol. 13, pp.400-412, 1965.
- Johnson, S.M., “Optimal Two and Three Stage Prouction Schedules with Setup Times Include,”Naval Research Logistics Quarterly,Vol. 1 No. 1, pp. 61-68, 1954.
- Kim, J.S., Kang, S.H.,and Lee, S.M., “ Transfer Batch Scheduling for a Two-Stage Flowshop with Identical Parallel Machines at Each Stage,” Omega,Vol. 25, No. 1, pp. 547-555, 1997.
- Lomnicki, Z.A., “A branch-and-bound algorithm for the exact solution of the three-machine scheduling problem”, Operational Research Quarterly, Vol. 16, pp.89-100, 1965.
- Maggu & Das, “On n x 2 sequencing problem with transportation time of jobs”, Pure and Applied Mathematika Sciences, 12-16, 1981.
- Yang, D.L. and Chern, M.S., “Two-Machine Flowshop Group Scheduling Problem,”Computers and Operations Research, Vol.27, No.10, pp.975- 985, 2000.
- Yoshida, T. and Hitomi, K., “Optimal Two-Stage Production Scheduling with Setup Times Separated,”AIIE Transactions, Vol. 11, No. 1, pp. 261-273, 1979
|