Research and Reviews - International Journals

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Optimization of linear antenna array using genetic algorithm for reduction in Side lobs levels and improving directivity based on modulating parameter M

Pallavi Joshi1, Nitin Jain 2, Rupesh Dubey3
  1. M.E. scholar , Dept. Of ECE, IES IPS Academy, Indore, India
  2. Associate Professor, Dept. Of ECE, IES IPS Academy, Indore, India
  3. Associate Professor & HOD, Dept. Of ECE, IES IPS Academy, Indore, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Side lobe and directivity of antenna array is main problem in radar and communication field. This paper describes linear antenna array radiation pattern in adaptive beam forming using genetic algorithm. Unlike Simple GA (SGA), Genetic Algorithm is an iterative stochastic optimizer that works on the population values based on the fitness value. This improves the performance of the maximum reduction in side lobe level with less no. of function calls and achieves the maximum directivity in the direction by modulating parameter M. This technique proved its effectiveness in improving the performance of the antenna array.



 

Keywords
Adaptive beam forming, Array factor, Directivity, Genetic algorithm, linear antenna array, Side lobe level.

INTRODUCTION
Usually the radiation pattern of a single element is relatively wide and each element provides low values of directivity. Antenna arrays increase the directivity without enlarging the size of single elements. Antennas arrays have been widely used in different applications are radar, sonar, and communications and as they are useful in high power transmission, reduce power consumption and enhanced spectral efficiency. Due to increased usage of electromagnetic spectrum, radiation pattern synthesis techniques, which allow placing of one or more nulls in the pattern in specified directions, are gaining technical importance. [1]. Array antennas have high gain and directivity compared to an individual radiating element [2]. Genetic algorithm (GA) is a powerful optimization method the synthesis of antenna array radiation pattern in adaptive beamforming. Adaptive beam forming is a signal processing technique in which the electronically steerable antenna arrays are used to obtain maximum directivity towards signal of interest (SOI) and null formation towards signal of not interest (SNOI) i.e. instead of a single antenna the antenna array can provide improved performance virtually in wireless communication [3]. The problem is to finding the weights of the antenna array elements that are optimum to provide the radiation pattern with maximum reduction in the sidelobe level and provide the maximum directivity towards the direction by modulating parameter M. The value of modulating parameter M is varying 0 to 1.the value of M is 0 when maximum directivity to a particular direction. When the value of M goes to high that time provide the radiation pattern with maximum reduction in sidelobe.

PROPOSED ALORITHM

A. GENETIC ALGORITHM
The genetic algorithm is a method for solving both constrained and unconstrained optimization problems that is based on natural selection, the process that drives biological evolution. The genetic algorithm repeatedly modifies a population of individual solutions. At each step, the genetic algorithm selects individuals at random from the current population to be parents and uses them produce the children for the next generation. You can apply the genetic algorithm to solve a variety of optimization problems that are not well suited for standard optimization algorithms, including problems in which the objective function is discontinuous, no differentiable, stochastic, or highly nonlinear.

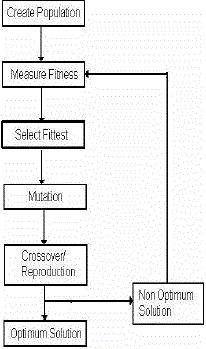
1. Genetic Algorithm Flowchart
The most common type of genetic algorithm works like this: a population is created with a group of individuals created randomly. The individuals in the population are then evaluated. The evaluation function is provided by the programmer and gives the individuals a score based on how well they perform at the given task.
Two individuals are then selected based on their fitness, the higher the fitness, the higher and the chance of being selected. These individuals then "reproduce" to create one or more offspring, after which the offspring are mutated randomly. This continues until a suitable solution has been found or a certain number of generations have passed, depending on the needs of the programmer.
Selection – this is based on the fitness criterion to choose which chromosome from a population will go on to reproduce
Reproduction – The propagation of individuals from one generation to the next.
Crossover – This operator exchanges genetic material which is the features of an optimization problem. Single point cross over is used here.
Mutation – The modification of chromosomes for single individuals. Mutation does not permit the algorithm to get stuck at local minimum.
Stopping criteria – The iteration stops when the maximum number of cycles is reached. The grand minimum CF and its corresponding chromosome string or the desired solution are finally obtained.
Population - the number of chromosomes considered in one generation.

B. Array Synthesis and solution:
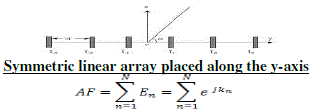
An incident plane wave causes a linear gradient time delay between the antenna elements that is proportional to the angle of incidence. This time delay along the array manifests as a progressive phase shift between the elements when it is projected onto the sinusoidal carrier frequency. In the special case of normal incidence of the plane wave, all the antennas receive exactly the same signal, with no time delay or phase shift. In this work the antenna elements are assumed to be uniformly spaced, in a straight line along the y-axis, and N is always the total number of elements in the antenna array. The physical separation distance is d, and the wave number of the carrier signal is k =2?/λ. The product kd is then the separation between the antennas in radians. When kd is equal to ?(or d= λ/2) the antenna array has maximum gain with the greatest angular accuracy with no grating lobes. The phase shift between the elements experienced by the plane wave is kdcosθand è is measured from the y-axis, starting from the first antenna, as shown in Fig1. Weights can be applied to the individual antenna signals before the array factor (AF) is formed to control the direction of the main beam. This corresponds to a multiple-input-single-output (MISO) system. . In the process of formulation for the fitness function for minimizing the Side lobe level the antenna array [4][5][6], the array factor for N number of elements were considered and assumed that the elements of an array are spaced linearly and separated by λ/2 where λ is the wave length.
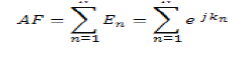image
Where En =ejkn and K= (nkdcosθ + βn) is the phase difference. βn is the phase angle. Consider an array of antenna consisting of N number of elements. It is assumed that the antenna elements are symmetric about the center of the linear array. The far field array factor of this array with an even number of isotropic elements (2N) can be expressed as
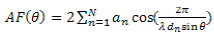image
Where amplitude of nth element, θ is the angle from broadside and is the distance between position of nth element and array center .The main objective of this work is to find an appropriate set of required element amplitude and that achieves interference suppression with maximum sidelobe level reduction. To find a set of values which produces the array pattern, the algorithm is used to minimize the following cost function
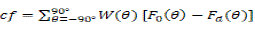image
WhereF0(θ) the pattern is obtained using our algorithm and is the pattern desired To find a set of values which produces the array pattern, the algorithm is used to minimize the following cost function
image
= abs (H) , Where H is normalized field strength
The maximum directive gain is called as directivity of the antenna. The directivity of the antenna is defined as the ratio of maximum radiation intensity to its average radiation intensity and is denoted by D.
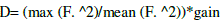image

EXPERIMENT AND RESULT
The antenna model consists of 8,16,20,24 elements and equally spaced with d =0.5λ along the y-axis. A continuous GA with a population size 20 and adaptive feasible mutation rate is run for a total of 100 generations unlike 500 generations as in using MATLAB and the best result was found for each iteration. The cost function is the minimum side lobe level for the antenna pattern and improving directivity by modulating parameter M. The value of modulating parameter M is varying 0 to 1.the value of M is 0 when maximum directivity to a particular direction. When the value of M goes to high that time provide the radiation pattern with maximum reduction in sidelobe.
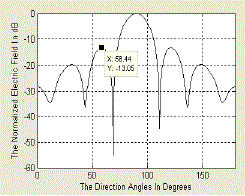
Fig 3 shows that the antenna array with N = 8 elements has been normalized for a gain of 2.84dB along the angle 0°, modulating parameter M value is 0(low), the maximum relative side lobe level of -13.05 dB and directivity 13.39.
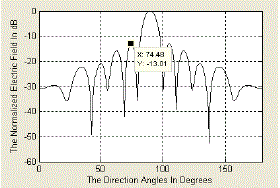
Fig 4 shows that the antenna array with N = 16 elements has been normalized for a gain of 2.84dB along the angle 0°, modulating parameter M value is 0(low), the maximum relative side lobe level of -13.01 dB and directivity 16.53.
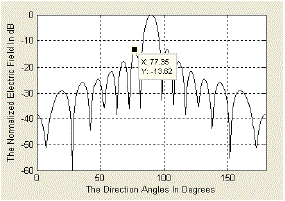
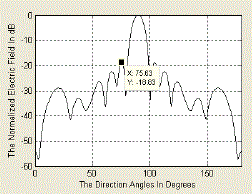
Fig 5 shows that the antenna array with N = 20 elements has been normalized for a gain of 2.84dB along the angle 0°, modulating parameter M value is 0(low), the maximum relative side lobe level of -13.62 dB and directivity 17.55.
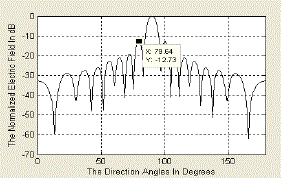
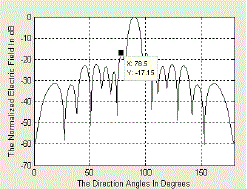
Fig 6 shows that the antenna array with N = 24 elements has been normalized for a gain of 2.84dB along the angle 0°, modulating parameter M value is 0(low), the maximum relative side lobe level of -12.73 dB and directivity 18.38
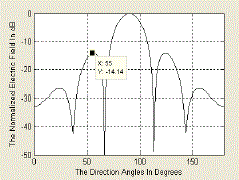
Fig 7 shows that the antenna array with N = 8 elements has been normalized for a gain of 2.84dB along the angle 0°, modulating parameter M value is 1(low), the maximum relative side lobe level of -14.14 dB and directivity 13.11.
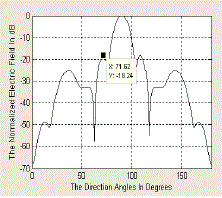
Fig 8 shows that the antenna array with N = 16 elements has been normalized for a gain of 2.84dB along the angle 0°, modulating parameter M value is 1(low), the maximum relative side lobe level of -18.24 dB and directivity 15.94.
Fig 9 shows that the antenna array with N = 20 elements has been normalized for a gain of 2.84dB along the angle 0°, modulating parameter M value is 1(low), the maximum relative side lobe level of -18.82 dB and directivity 16.56.
Fig 10 shows that the antenna array with N = 16 elements has been normalized for a gain of 2.84dB along the angle 0°, modulating parameter M value is 1(low), the maximum relative side lobe level of -18.24 dB and directivity 15.94.

CONCLUSION
In this paper Genetic algorithm Solver in Optimization toolbox of MATLAB is used to obtain maximum reduction in side lobe level relative to the main beam on both sides of 0° and improve the directivity by modulating parameter M. The genetic algorithm is a method for solving both constrained and unconstrained optimization problems that is based on natural selection, the process that drives biological evolution. Adaptive feasible mutation with single point crossover showed the performance improvement by reducing the side lobe level below -10dB in most of the cases and also improves the directivity. The best result of -18.82.05 dB sidelobe is obtained for 20 elements in 100 generation of GA with best fitness value of 88.2984 and means fitness value of 91.2427and the best result of 18.38 directivity is obtained for 24 elements.

Tables at a glance
Table icon Table icon
Table 1 Table 2

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 6 Figure 7 Figure 8 Figure 9 Figure 10
Figure 6 Figure 7 Figure 8 Figure 9 Figure 10

References