International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

PAPR Reduction in Multicarrier Modulations Using Firefly Algorithm

Aman Dhillon1, Sonia Goyal2
  1. M.Tech Student, Department of Electronics and Communication Engineering, UCoE Patiala, Punjab, India
  2. Assistant Professor, Department of Electronics and Communication Engineering, UCoE Patiala, Punjab, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Orthogonal frequency division multiplexing (OFDM) technique is a promising technique in this regard as it offers high data rate and reliable communications over various fading channels. But the main drawback of OFDM is the high peak to average power ratio (PAPR). In this paper we proposed the technique to reduce the PAPR using Firefly algorithmin in multicarrier modulation system. Simulation results show that the proposed scheme considerably outperforms the conventional system.



 

Keywords
Orthogonal Frequency Division Multiplexing (OFDM), Peak to Average Power Ratio (PAPR), multicarrier modulation, Firefly algorithm.

INTRODUCTION
OFDM technology is a special Multi-Carriers Modulation transmission scheme which can be seen as either a modulation technology or a multiplexing technology. It has so many advantages that other wireless communication technology cannot compete with due to its resistance to frequency selective fading and narrow-band interference [1]. Meanwhile, it is also a parallel technology which separate high-speed data stream into many low-speed data stream to achieve a data rate of high speed transmission. Since the rate of each code element is low, the signal period is relatively long, and thus it has a stronger resistance to delay spread than conventional technologies. Besides, because of the adoption of cyclic prefix as a guard interval [2], more inter-symbol interference can be significantly reduced and thus overcome the channel delay spread caused by inter-symbol interference. To summarize, it would be a valuable transmission technology with high efficiency to wireless communications with limited resources.
On the other hand, a difficulty about OFDM signals is the fact that they have a very large peak-to-average power ratio which is in urgent need to be solved. This property of OFDM leads to a high requirement of AD or DA converter and high power amplifier (HPA). The required HPA should have a large linear dynamic range, so its cost must be very high. To transmit the large peaks at the tails of the distribution, the HPA must support a very large dynamic range, which is either impractical or expensive. Transmitting filtering and D/A conversion further complicate the PAPR problem. However, since the appearance of peak power is random, the linear amplifier must not have been working in the most efficient state, resulting in low power efficiency. Power amplifier nonlinear distortion results in intermodulation distortion and adjacent channel interference, which affect the performances of communication system directly [3].
So, hunting for measures to reduce peak-to-average ratio of OFDM signals became more and more important. The previous work is based on codes and genetic algorithms. This paper mainly focuses on PTS method of reducing PAPR using firefly algorithm, and then analyze conventional schemes through Matlab simulation.
The paper is organized as follows: Section I, presents brief introduction about OFDM. Section II, introduces about the partial transmit sequence technique. Section III, describes Firefly algorithm. Section IV, includes the simulation results. Section V, concludes the results of work.

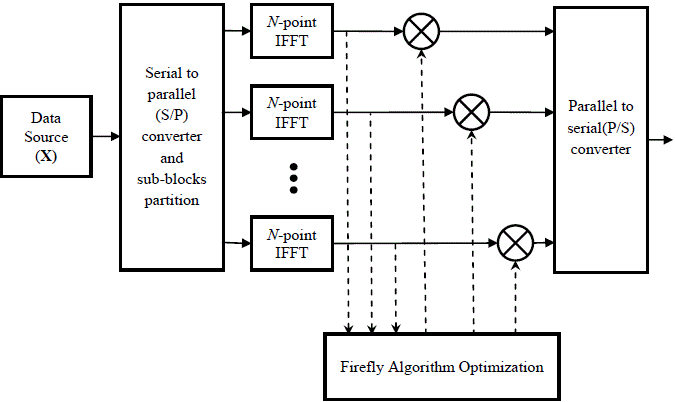
PARTIAL TRANSMIT SEQUENCE
Several methods have been proposed to reduce PAPR [4]. Among them, Partial Transmit Sequence (PTS) [5] is known as distortionless scheme which require a small amount of redundancy. The PTS approach is based on merging signal sub-blocks which are opportunely phase shifted as to reduce PAPR. A drawback of PTS is that requires multiple inverse fast Fourier/wavelet transforms (IFFT/IDWT), thus resulting in high computational complexity in practical systems. If M is the number of sub-blocks and W the number of phase shifts the computational burden of PTS increases. In general, the complexity of PTS is proportional to the number of the candidate signals. Therefore, to reduce the complexity, some simplified techniques have been proposed [6]–[9] aiming at reducing the number of candidate signals. In [6], the candidate signal can be transmitted directly without an exhaustive search when its PAPR is lower than a preset threshold. In [7] a new algorithm for computing the phase factors that achieves better performance than the Optimal Binary Phase Sequence search approach is presented. A new algorithm based on Fincke Phost Sphere Decoder is proposed in [8], where only those phase vectors that guarantee that the PAPR is bounded are searched. In the technique proposed in [9] a gradient descent search is performed to find the phase factors. In this work we propose a complexity reduction of PTS optimization using Genetic Algorithms[10].

FIREFLY ALGORITHM
In the firefly algorithm, the objective function of a given optimization problem is based on differences in light intensity. It helps the fireflies to move towards brighter and more attractive locations in order to obtain optimal solutions. All fireflies are characterized by their light intensity associated with the objective function. Each firefly is changing its position iteratively. The firefly algorithm has three rules [12], [13], [14].
? All fireflies are unisex, and they will move towards more attractive and brighter ones.
? The attractiveness of a firefly is proportional to its brightness which decreases as the distance from the other firefly increases. If there is not a more attractive firefly than a particular one, it will move randomly.
? The brightness of a firefly is determined by the value of the objective function. For maximization problems, the brightness is proportional to the value of the objective function.
Each firefly has its attractiveness ?? described by monotonically decreasing function of the distance r between two any fireflies [1]:
image
Where??0 denotes the maximum attractiveness (at r = 0) and is the light absorption coefficient, which controls the decrease of the light intensity. The distance between two fireflies i and j at positions xi and xj can be defined as follows [12]:
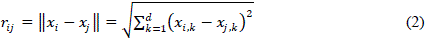image
Where ????,?? is the k-th component of the spatial coordinate xi of i-th firefly and d denotes the number of dimensions. The movement of a firefly i is determined by the following form [1].
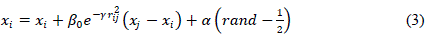image
Where the first term is the current position of a firefly i, the second term denotes a firefly?s attractiveness and the last term is used for the random movement if there are not any brighter firefly (rand is a random number generator uniformly distributed in the range < 0, 1 >). For most cases ?? ∈ (0, 1), ??0 = 1. In practice the light absorption coefficient ?? varies from 0.1 to 10. This parameter describes the variation of the attractiveness and its value is responsible for the speed of FA convergence [13].
The firefly algorithm can be presented in the following pseudo-code form [13], [14].
1. Initialize algorithm?s parameters:
? Number of fireflies (n),
β0,γ,α
? Maximum number of generations (iterations, Max-Gen).
2. Define the objective function f(x), x = (x1. . ., xd)T.
3. Generate initial population of fireflies xi(i = 1, 2. . .,n). Light intensity of firefly Ii at xiis determined by value of objective function f(xi).
4. Whilek<MaxGen
5. For i = 1:n
6. For j = 1:i
7. If (Ij> Ii) move firefly i towards firefly j in d-dimension according to Eq. (3); End if
8. Obtain attractiveness, which varies with distance r according to Eq. (1).
9. Find new solutions and update light intensity
10. End for j.
11. End for i.
12. Rank the fireflies and find the current best
13. End while
14. Find the firefly with the highest light intensity.
The initial population of fireflies is generated in the following form:
image
Where LB and UB denotes the lower and the upper bounds of i-th firefly. After the evaluation of the initial population the firefly algorithm enters its main loop, which represents the maximum number of generations of the fireflies (iterations). For each generation the firefly with the maximum light intensity (the solution with the best value of objective function) is chosen as the potential optimal solution). The firefly algorithm simulates parallel run strategy. The population of n fireflies generates n solutions.

SIMULATION RESULTS
Parameters Setting for Matlab Simulations
The following Table I illustrates the parameter name and value used for MATLAB simulation of the system model. Parameter description is given along with.
B. System Performance (CCDF Vs. PAPR)
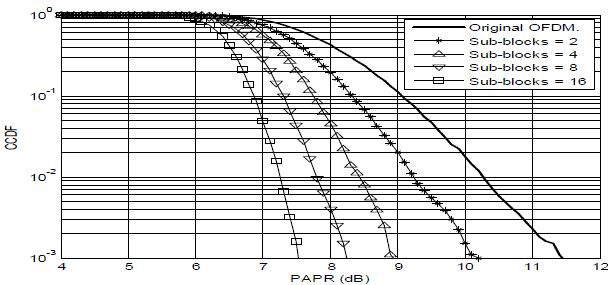
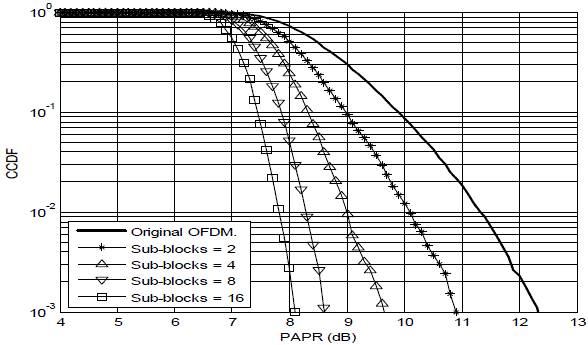
Fig. 2 to 4 illustrates the CCDF vs. PAPR performance of the system described. The parameter settings for the system model and the Firefly algorithm are given in Table I. The only difference being in the number of subcarriers N (128, 256, and 512) used and the underlying modulation used (16-QAM). In each simulation the number of sub-blocks are varied from 2, 4, 8 and 16, whereas the number of possible phase shifts are varied from 0 to 2π. The phase shift values between 0 and 2π are obtained using Firefly algorithm.
Fig.2. illustrates the system performance (CCDF vs. PAPR) for underlying 16-QAM modulation and N=128 subcarriers. It can be seen that by increasing the number of sub-blocks PAPR reduces significantly. At CCDF of 10-2 PAPR is 8.8 dB for 2 sub-blocks, 7.9 dB for 4 sub-blocks, 7.3 dB for 8 sub-blocks and 6.7 dB for 16 sub-blocks. Moreover, a reduction of about 0.9 dB with respect to the original OFDM (without sub-blocks or rather 1 sub-block) is achieved if compared with PAPR of 2 sub-blocks. If number of subcarriers is 256 then PAPR is increased as compared to number of subcarriers 128.
At CCDF of 10-2 PAPR is 9.2 dB for 2 sub-blocks, 8.4 dB for 4 sub-blocks, 7.8 dB for 8 sub-blocks and 7.3 dB for 16 sub-blocks. If number of subcarriers is 512 then PAPR is increased as compared to number of subcarriers 256. At CCDF of 10-2 PAPR is 10.1 dB for 2 sub-blocks, 9.0 dB for 4 sub-blocks, 8.2 dB for 8 sub-blocks and 7.8 dB for 16 sub-blocks From the above figures it can be noted that there is significant improvement with increase in the number of sub-blocks and modulation. With increase in the number of subcarriers the system performance degrades as shown in figure 2 to 4. With increase in number of subcarriers PAPR is increased.

CONCLUSION
In this paper we have proposed the use of Firefly Algorithm in conjunction with PTS to reduce PAPR in multi-carrier modulation systems. Firefly Algorithm was used with PTS technique to reduce the PAPR of OFDM signals. Simulations were conducted and show that the performance of the proposed FF-PTS system provided almost the same PAPR statistics as that of the optimal exhaustive PTS, while maintaining a low computational load. Results show the effectiveness of the proposed method in reducing the computational complexity of the PTS algorithm. The proposed FF-PTS technique provides a practical approach toward solving the difficulty of high PAPR in OFDM systems.

ACKNOWLEDGMENT
The Authors appreciate the Help given by the guide Mrs. Sonia Goyal and Electronics & Communication Department, Punjabi university Patiala for the Technical Assistance.

Tables at a glance
Table icon
Table 1

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4
Figure 1 Figure 2 Figure 3 Figure 4

References