International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

PAPR Reduction in Multi-User MIMOOFDM

B.Ragadivya1, Dr.T.Sreenivasulu Reddy2
  1. M.Tech Student, Department of ECE, SVU College of Engineering, Andhra Pradesh, India
  2. Associate Professor, Department of ECE, SVU College of Engineering, Andhra Pradesh, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Orthogonal Frequency Division Multiplexing (OFDM) is a multi -carrier transmission method which is most broadly used in the field of communication. One of the main drawback of this scheme is Peak to Average Power Ratio (PAPR). There are various methods introduce for the reduction of PAPR in OFDM. However these technique have major disadvantage that they reason non -linear in-band deformation and out-of-band emission, this reduces the scheme throughput. Thus, Multi-Input and Multi output, which is the proposed technique discussed in our statement overcome this trouble. In this method, we replace some of the transmit data symbols by nulls, i.e. we introduce errors in the transmitted signal. At the receiver, an iterative decoder is used to correct the spreader and channel errors. Particularly, we suggest to together carry out MU pre-coding, OFDM cadence, and PAR lessening by solving a convex optimization trouble. We develop a matching fast iterative truncation algorithm (FITRA) and show arithmetical results to show marvelous PAR-reduction competence. The appreciably summary linearity supplies eventually permit the use of cut-rate RF components for the large-scale MU-MIMO-OFDM system.

 

Keywords
OFDM, PAPR, Switching and Shifting of Null Sub-Carriers

INTRODUCTION
After more than thirty years of research and growth carried out in the field of communication OFDM has been widely implemented in high speed digital communication [1]. OFDM has its major benefits of higher data rates and better performance. The higher data rates are achieved by use of multiple carriers and performance improved by use of guard interval which leads to removal of Inter Symbol intrusion (ISI) [2]. OFDM has several features which makes it more advantageous for high speed data transmission. These features include High Spectral competence, Robustness to Channel Fading, and Immunity to Impulse Interference, litheness and Easy Equalization. In spite of these benefits there are some drawbacks such as PAPR, Offset frequency and Inter Carrier meddling (ICI) between sub-carriers [3]. Practical wireless channels typically exhibit frequency selective fading and a low-PAR precoding solution suitable for such channels would be desirable. Rather, the solution should be such that the complexity required in each (mobile) terminal is small (due to stringent area and authority constraints), whereas heavier dispensation could be afforded at the BS. Orthogonal frequency-division multiplexing (OFDM) [8] is an efficient and well-established way of commerce with frequency selective channels. In addition to simplify the equalization at the receiver, OFDM also facilitates pertone influence and bit allocation, scheduling in the frequency domain, and band shaping. However, OFDM is known to suffer from a high PAR [9], which necessitate the use of linear RF components (e.g., power amplifiers) to avoid out-ofband radiation and signal distortions. Unfortunately, linear RF components are, in general, more costly and less power efficient than their non-linear counterparts, which would eventually result in exorbitant costs for large-scale BS implementations having hundreds of antennas. Therefore, it is of paramount consequence to reduce the PAR of OFDMbased large-scale MU-MIMO s to facilitate parallel low-cost and low-power BS implementations.
A. Contributions
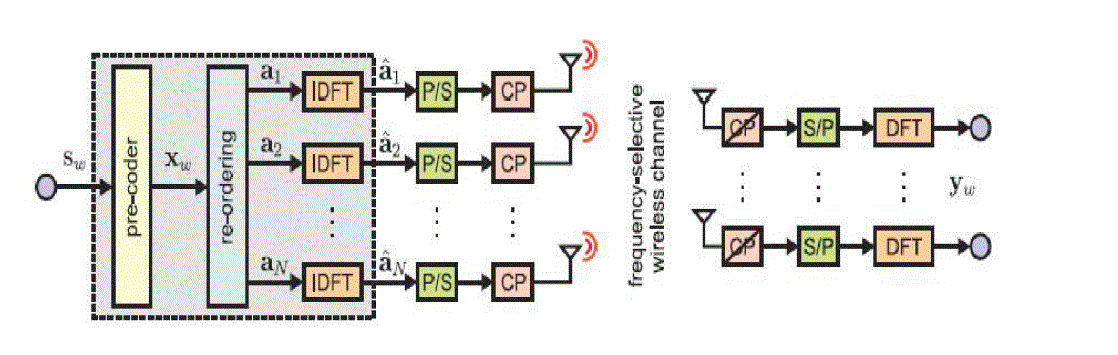
In this paper, we develop a novel system broadcast scheme for large-scale MU-MIMO-OFDM wireless s, which only affects the signal processing at the BS while leaving the meting out required at each terminal undamaged. The key idea of the proposed scheme is to exploit the excess of degrees-of-freedom (DoF) offered by equip the BS with a large number of antennas and to jointly perform MU precoding, OFDM modulation, and PAR reduction, referred to as PMP in the remnants of the paper. Our contributions can be summarized as follows:We formulate PMP as a convex optimization problem, which in cooperation performs MU precoding, OFDM modulation, and PAR reduction at the BS. •We develop and examine a novel optimization algorithm, referred to as fast iterative truncation algorithm (FITRA), which is able to find the solution to PMP efficiently for the (typically large) dimensions arising in large-scale MU-MIMO-OFDM.We present numerical simulation results to demonstrate the capability of the proposed MUMIMO- OFDM system spread scheme. Specifically, we analyze the trade-offs between PAR, error-rate performance, and out-of-band radiation, and we present a comparison with conventional preceding schemes. b. Notation lowercase bold-face writing for column vectors and upper-case bold-face letters designate matrix. The M×M distinctiveness matrix is denoted by Im. The M×N all zeros matrixes by 0m×n. and Fm refers to the M×M discrete Fourier transform(DFT) matrix.
b. Outline of the Paper
The remainder of the paper is organized as introduces the model and summarizes important PAR-reduction concepts. The proposed system transmission scheme is detailed and the fast iterative truncation algorithm (FITRA) is developed.

PEAK TO AVERAGE POWER RATIO

A. PAPR Problem
One of the new problems emerging in OFDM s is the so-called Peak to Average Power Ratio (PAPR) problem. The input symbol stream of the IFFT should possess a uniform power spectrum, but the output of the IFFT may result in a non-uniform or spiky power spectrum. Most of transmission energy would be allocated for a few instead of the majority subcarriers. This problem can be quantified as the PAPR measure. It causes many problems in the OFDM at the transmitting end.
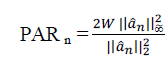image

B. Effect of PAPR
There are some obstacles in using OFDM in transmission in contrast to its advantages [3]:
(i) A major obstacle is that the OFDM signal exhibits a very high Peak to Average Power Ratio (PAPR).
(ii) Therefore, RF power amplifier should be operated in a very large linear region. Otherwise, the signal peaks get into non-linear region of the power amplifier causing signal distortion. This signal deformation introduces intermediation among the subcarriers and out of band radiation. Thus, the power amplifiers should be operated with large power back offs. On the other hand, this leads to very inefficient amplification and expensive transmitters. Thus, it is highly desirable to reduce the PAPR.
(iii) These large peaks cause saturation in power amplifiers, leading to inter modulation products among the subcarriers and disturbing out of band energy. Therefore, it is desirable to reduce the PAPR.
(iv) To reduce the PAPR, several techniques have been proposed such as clipping, coding, peak windowing, Tone Reservation and Tone Injection. But, most of these methods are unable to achieve simultaneously a large reduction in PAPR with low complexity, with low coding overhead, without performance degradation and without transmitter receiver symbol handshake.
(v) Complexity is increased in the analog to digital and digital to analog converter.

PROPOSED TECHNIQUES

PAPR Reduction Techniques
The PAPR is considered as one of the major disadvantage in the multicarrier communication s. In order to reduce and eliminate these problems many different methods are proposed. These methods are classified into various categories. All the proposed methods mainly aim at reducing the PAPR as much as possible and along with it they take care not to interrupt and disturb the other parts of the . The algorithms considered while reduction should not be complex and easily implementable. Following are the categories of PAPR reduction.
The proposed system transmission scheme, referred to as PMP, combines MU precoding, OFDM modulation, and PAR reduction.

Trans parent Methods
In this category the receiver does not know about the method that the transmitter has applied. The same thing takes place when it comes to the receiver. The transmitter also does not necessarily know about the method that the receiver is using. In order to remove MUI, the signal vectors sw, ∀w are passed through a precoder, which generates W vectors xw∈CN according to a given precoding scheme (see Section II-B). Since precoding causes the transmit power P = _W w=1 _xw_2 2 to depend on the signals sw, ∀w and the channel state, we normalize the precoded vectors xw, ∀w prior to transmission as
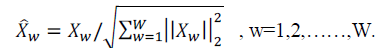image
which ensures unit transmit power. We emphasize that this normalization is an essential step in practice (i.e., to meet regulatory power constraints). To simplify the presentation, however, the normalization is omitted in the description of the precedes to follow (but normalization is employed in all simulation results shown in Section V). Hence, in what follows xwand ˆxware treated interchangeably.
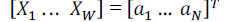image
Here, the W-dimensional vector ancorresponds to the (frequency-domain) signal to be transmitted from the nth antenna. The time-domain samples are obtained by applying the inverse DFT (IDFT) according to ˆan = FH Wan followed by parallel-to-serial (P/S) conversion. Prior to modulation and transmission over the wireless channel, a cyclic prefix (CP) is added to the (time-domain) samples ˆan, ∀n to avoid ISI. To simplify the exposition, we specify the input- output relation of the wireless channel in the frequency domain only.Concretely, we consider
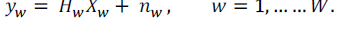image

MU Preceding Schemes
In order to avoid MUI, precoding must be employed at the BS. To this end, we assume the channel matrices, ∀w to be known perfectly at the transmit-side.3 Linear precoding now amounts to transmitting xw= Gwsw, where Gw∈CN×M is a suitable precoding matrix. One of the most prominent precoding schemes is least-squares (LS) precoding (or linear zero-forcing precoding), which corresponds to Gw= H†w. Since HwH†w = IM, transmittingxw= H†wswperfectly removes all MUI, i.e., it transforms (3) into M independent single-stream systems yw= sw+ nw. Note that LS precoding
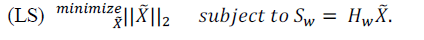image
This formulation inspired us to state the MU-MIMO-OFDM downlink transmission scheme proposed in Section III as a convex optimization problem is equivalent to transmitting the solution x˙ w to the following convex optimization problem.

SIMULATION RESULTS
In this section, we demonstrate the efficacy of the proposed joint precoding, modulation, and PAR reduction approach, and provide a comparison to conventional MU precoding schemes.

A. Simulation Parameters
Unless explicitly stated otherwise, all simulation results are for a MU-MIMO-OFDM havingN = 100 antennas at the BS and serving M = 10 single-antenna terminals. We employ OFDM with W = 128 tones and use a spectral map T as specified in the 40MHz-mode of IEEE 802.11n [20].10 We consider coded transmission, i.e., for each user, we independently encode 216 information bits using a convolution code (rate-1/2, generator polynomials [133o 171o], and constraint length 7), apply random interleaving (across OFDM tones), and map the coded bits to a 16-QAM constellation (using Gray labeling). To implement (PMP-L), In addition to LS and MF precoding, we also consider the performance of a baseline precoding and PAR-reduction method. To this end, we employ LS precoding followed by truncation (clipping) of the entries of the time-domain samples ˆan, ∀n. We use a clipping strategy where one can specify a target PAR, which is then used to compute a clipping level for which the PAR in (4) of the resulting timedomain samples is no more than the chosen target PAR.

B. Performance Measures
CCDF computes the power complementary cumulative distribution (CCDF) function from a time domain signal. The CCDF curve shows the amount of time a signal spends above the average power level of the measured signal, or equivalently, the probability that the signal power will be above the average power level.To compare the PAR characteristics of different precoding schemes, we use the complementary cumulative distribution function (CCDF) defined as
CCDF (PAR) = P{PARn> PAR}.
We furthermore define the “PAR performance” as the maximum PAR level PAR∗ that is met for 99% of all transmitted OFDM symbols, i.e., given by CCDF(PAR∗ ) = 1%. The error-rate performance is measured by the average (across users) symbol-error rate (SER); a symbol is said to be in error if at least one of the information bits per received OFDM symbol is decoded in error. The “SNR operating point” corresponds to the minimum SNR required to achieve 1% SER. In order to characterize the amount of signal power that is transmitted outside the active tones.
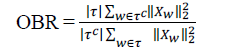image

C. Summary of PMP Properties
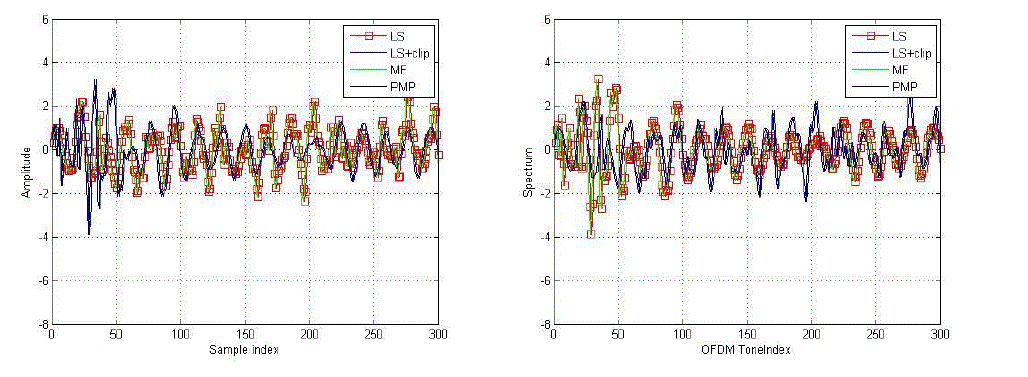
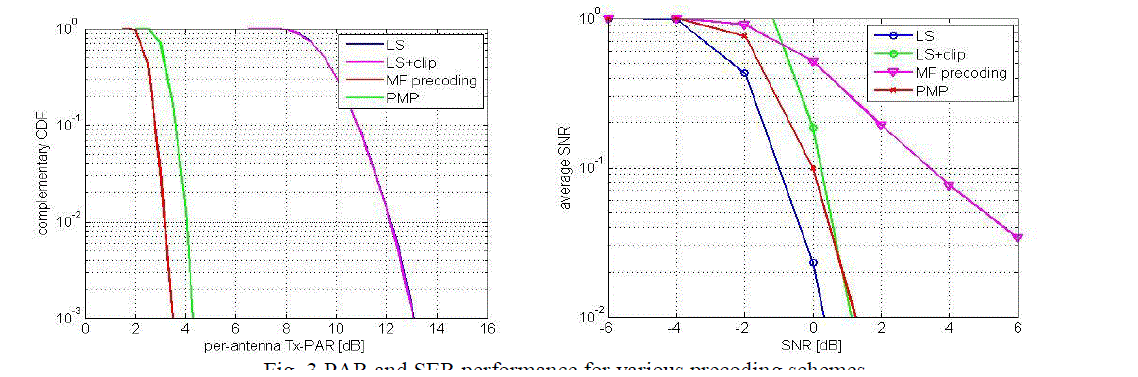
Figures 2 and 3 summarize the key characteristics of PMP and compare its PAR-reduction capabilities and error-rate performance to those of LS and MF precoding, as well as to LS precoding followed by clipping (denoted by “LS+clip” in the following). The real part of a time domain signal ˆa1 for all precoding schemes (the imaginary part behaves similarly). Clearly, PMP results in time-domain signals having a significantly smaller PAR than that of LS and MF; for LS+clip the target PAR corresponds to 4 dB.The frequency-domain results. The PAR-performance characteristics for all consideredprecoding schemes. One can immediately see that PMP reduces the PAR by more than 11 dB compared to LS and MF precoding (at CCDF(PAR) = 1%); as expected, LS+clip achieves 4 dB PAR deterministically. In order to maintain a constant transmit power, the signals resulting from PMP require a stronger normalization (roughly 1 dB) than the signals from LS precoding; this behavior causes the SNR-performance loss compared to LS The performance loss of MF and LS+clip is mainly caused by residual MUI. It is important to realize that even if LS+clip outperforms PMP in terms of the PAR/SNR trade-off in the high-PAR regime, LS+clip results in substantial out-of-band interference; this important drawback is a result of ignoring the shaping constraints (7). In particular, we can observe from that reducing the PAR for LS+clip quickly results in significant OBR, which renders this scheme useless in practice. By way of contrast, the OBR of PMP is significantly lower and degrades gracefully when lowering the PAR. Furthermore, we see that reducing the maximum number of FITRA iterations K increases the OBR. Hence, the regularization parameter λ together with the maximum number of FITRA iterations K determine the PAR. In this communication may be used for data transmission for source to destination to reduction of peak average power ratio. In a modulation technique modulation is a process in which the characteristics of a carrier wave is varied in accordance with the instant nous values of a message signal or modulating signal. In this proposed may be used for the reduction of PAPR by using multi input and multi output communication technique. In this process by using orthogonal frequency de-multiplexing technique is used for large band width communication for transmission and receiver section. In main advantage of BER rate decreases the both transmission and reception for a communication process.
The target PAR for LS+clip is 4 dB and λ = 0.25 for PMP relying on FITRA. (a) Time-domain signals (PAR: LS = 10.4 dB, LS+clip= 4.0 dB, MF = 10.1 dB, and PMP = 1.9 dB). Note that PMP generates a time-domain signal of substantially smaller PAR than LS and MF. (b) Frequency-domain signals (OBR: LS = −∞dB, LS+clip= −11.9 dB, MF = −∞dB, and PMP = −52.9 dB). Note that LS, MF, and PMP preserve the spectral properties. LS+clipsuffers from substantial OBR (visible at both ends of the spectrum).
The target PAR for LS+clip is 4 dB and λ = 0.25 for PMP relying on FITRA. (a) PAR performance (the curves of LS and MF overlap). Note that PMP effectively reduces the PAR compared to LS and MF precoding. (b) Symbol error-rate (SER) performance. Note that the signal normalization causes 1 dB SNR-performance loss for PMP compared to LS precoding. The loss of MF is caused by residual MUI; the loss of LS+clip is caused by normalization and residual MUI.

CONCLUSIONS AND OUTLOOK
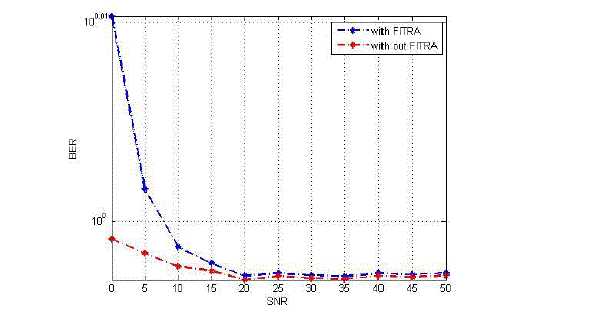
The proposed joint precoding, modulation, and PAR reduction framework, referred to as PMP, facilitates an explicit trade-off between PAR, SNR performance, and out-of-band interference for the large-scale MU-MIMO-OFDM system. As for the constant-envelope precoder in [7], the fundamental motivation of PMP is the large number of DoF offered by s where the number of BS antennas is much larger than the number of terminals (users). Essentially, the system channel matrix has a high-dimensional null-space, which enables us to design transmit signals with “hardware-friendly” properties, such as low PAR. In particular, PMP yields perantenna constant-envelope OFDM signals in the largeantenna limit, i.e., for N →∞. PMP is formulated as a convex optimization problem for which a novel efficient numerical technique, called the fast iterative truncation algorithm (FITRA), was devised. Numerical experiments showed that PMP is able to reduce the PAR by more than 11 dB compared to conventional precoding methods, without creating significant out-of-band interference; this substantially alleviates the linearity requirements of the radiofrequency (RF) components. Furthermore, PMP only affects the signal processing at the BS and can therefore be deployed in existing MIMO-OFDM wireless communication s, such as IEEE 802.11n [20]. In addition to the extensions outlined in Section III-D, there are many possibilities for future work. Analytical PAR performance guarantees of PMP are missing; the development of such results is challenging and part of ongoing work. Over, a detailed analysis of the impact of imperfect channel state information on the performance of PMP is left for future work. Finally, further reducing the computational complexity of FITRA, e.g., using continuation strategies , is vital for a practical realization of PMP in hardware.
To reduce bit error rate and to cover large area for multi input and multi output channel.

CONCLUSIONS
To reduce the PAPR of multi-carrier transmission, this proposed scheme reorders the null-subcarriers and data subcarriers. This new method shifts the “innermost” null sub - carriers among different data-subcarriers to minimize the PAPR. The proposed method is distortion less, does not affect the constellation at the data-subcarriers, maintains better PAPR reduction and BER reduction performance while keeping low computational complexity, needs less CSI, can collaborate with most other PAPR-reduction methods, and can be compatible with existing standards. The Shifting/Switching method can also be coupled with other PAPR reduction techniques since the conventional methods do not alter the null sub-carriers which are used in the shifting process.

Figures at a glance
Figure Figure Figure Figure
Figure 1 Figure 2 Figure 3 Figure 4

References